目的
今回は、ダイオード・リング変調器(Diode Ring Modulator)を取り上げます。その原理や用途を説明した上で、実際に回路を構築して動作を確認します。また、抑圧搬送波両側波帯(DSBSC:Double-sideband Suppressed-carrier)信号の生成方法について解説を加えます。
準備するもの
- アクティブ・ラーニング・モジュール「ADALM2000」
- ソルダーレス・ブレッドボード
- ジャンパ線キット
- 抵抗:100Ω(4個)、1kΩ(2個)
- ダイオード:「1N914」(4個)
- トランス:トリファイラ巻きのものを使用できる場合(2個)
背景
電子通信の分野において、平衡変調器はDSBSC信号を生成するために使用されます。同変調器の回路は、無線周波数の搬送波信号を抑圧しつつ、搬送波信号と変調信号(変調の対象になる元々の信号)の和と差の周波数成分を出力します(詳細は後述)。つまり、出力信号には搬送波そのものの周波数成分は含まれません。その一方で、従来のAM(Amplitude Modulation)信号に含まれる情報はすべて保持されます。この方法を使用すれば、信号の伝送に伴う電力を削減できます。
平衡変調器の非常に一般的な実装の1つがダイオード・リング変調器です。この種の回路は、格子変調器(Lattice Modulator)とも呼ばれます。ダイオード・リング変調器は、リング状に配置された4個のダイオード(名称の由来)と、入力トランス、出力トランスで構成されます(図1)。この変調器には2つの信号が入力されます。1つは単一周波数の搬送波信号です。もう1つは、単一周波数または様々な周波数成分から成る複雑な波形の変調信号です。搬送波信号は、入力トランスと出力トランスのセンター・タップに入力されます。一方、変調信号は入力トランスの1次側に印加されます。その結果、出力トランスの2次側に現れるのが出力信号(DSBSC信号)です。図1には、ダイオード・リング変調器の2種類の構成方法を示してあります。
ダイオード・リング変調器は、電子通信の分野で広く使用されています。その用途はDSBSC信号の生成に限りません。例えば、周波数変調(Frequency Modulation)システムや位相変調(Phase Modulation)システムでも使われます。それだけでなく、位相偏移変調 (PSK:Phase-shift Keying)や直交位相振幅変調(QAM:Quadrature Amplitude Modulation)などに対応するデジタル変調システムでも使用されます。
ダイオード・リング変調器のダイオードの配置については注意が必要です。ブリッジ整流器におけるダイオードの配置もよく似たリング形状ですが、それと混同しないようにしてください。図1(a)のダイオード・リング変調器では、すべてのダイオードが時計回りまたは反時計回りに並んでいます。一方、ブリッジ整流器では、すべてのダイオードが右または左に向いています。
動作
一般に、ダイオード・リング変調器で使用されるのは、シリコン・ベースのダイオード、シリコン・ベースのショットキー・バリア・ダイオード、GaAs(ガリウム・砒素)ベースのダイオードのうちいずれかです。それらは、入力信号が通過する際、位相を180°変化させる(反転させる)か否かを制御するスイッチとして機能します。ダイオードを高速でオン/オフさせる役割を果たすのが搬送波信号です。ダイオード・リング変調器が動作するには、搬送波信号の振幅が変調信号の振幅よりも十分に大きくなければなりません。具体的には約6~7倍の振幅が必要です。
ここで、図2をご覧ください。これは、ダイオード・リング変調器の正の半サイクルの動作を表したものです。このサイクルでは、ダイオードD1と同D2が順方向にバイアスされてオンの状態になります。一方、ダイオードD3と同D4は逆バイアスされ、オープン・サーキットとして振る舞います。搬送波信号に伴う電流は、入力トランスの2次側のセンター・タップで均等に分割され、巻線の上半分と下半分を逆方向に流れます。そして、上半分と下半分の各電流により、強さが等しく互いに逆向きの磁界が生成されます。生成された磁界は互いに打ち消し合うことから、搬送波信号が抑圧されることになります。一方、変調信号は入力トランスからD1とD2を介して位相が反転しない状態で出力トランスへと伝送されます。
続いて、図3をご覧ください。これは、ダイオード・リング変調器における負の半サイクルの動作を表したものです。このサイクルにおいて、D1とD2は逆方向にバイアスされてオフの状態になります。一方、D3とD4は順方向にバイアスされてオンの状態になります。搬送波に伴う電流の振る舞いは、正の半サイクルにおける振る舞いと似たようなものになります。すなわち、その電流は出力トランスの1次側で均等に分割されます。そして、2つの電流によって強さが等しく互いに逆向きの磁界が生成されます。2つの電流は入力トランスの2次側で合流し、2つの磁界は互いに打ち消し合います。その結果、搬送波信号が抑圧されます。変調信号は入力トランスを通過しますが、出力トランスに到達する前に位相が反転します。
図4に、ダイオード・リング変調器の各信号波形を示しました。
出力信号としては、搬送波信号が抑圧されて2つの入力信号の和と差の成分だけが現れます。それらの出力信号は、搬送波信号のレートで変調信号の形状と振幅を表現するRFパルスだと捉えればよいでしょう。理想状態において、搬送波信号は完全に抑圧されて出力信号には現れません。しかし、実際にはそうはなりません。出力信号には、わずかではあるものの搬送波の成分が必ず含まれます。この現象をキャリア・リークと呼びます。キャリア・リークが生じる原因は2つあります。1つは、トランスのセンター・タップの位置のずれです。つまり、現実のトランスでは中央の位置にセンター・タップを厳密に設定できるわけではなく、ある程度の誤差が伴うということです。もう1つの原因は、現実のダイオードを複数使用する場合に生じるミスマッチです。
ハードウェアの設定
図5に示すのが、実習用に用意したダイオード・リング変調器の回路です。これをソルダーレス・ブレッドボード上に実装すれば、その動作を確認できます。リング状に配置するダイオードとしては、スイッチングが高速な「1N914」を使用します。ADALM2000の任意波形ジェネレータ(AWG)のチャンネル1(W1)は、ピークtoピークの振幅が1V、周波数が1kHzの正弦波を生成するように設定してください。この正弦波が変調信号に相当します。また、AWGのチャンネル2(W2)は、ピークtoピークの振幅が6V、周波数が10kHzの正弦波を生成するように設定してください。この正弦波が搬送波に相当します。入力トランスと出力トランスの巻線比は1:2です。巻線比が異なる他のトランスを使用して、出力結果を比較してみてもよいでしょう。この実習では、トランスとして「Hexa-Path Magnetics」(Coilcraft製)を使用します。巻線レイアウトについては、HP3、HP4、HP5、HP6のうちいずれかを選択します。これらのトランスを入手できない場合、「LTspice®」によるシミュレーションで動作を確認してください。
手順
図5の回路の出力波形を観測してください。図6に示したシミュレーション結果と同様の波形が得られるはずです。
先述したように、入力トランスと出力トランスの巻線比を変更してみてください。その上で出力波形を観測し、変更前の結果と比較しましょう。また、回路においてW1とW2の接続を入れ替えてみてください。変更前と比較して、出力波形はどのように異なるのか確認しましょう。
簡素化したダイオード・リング変調器
続いて、ダイオード・リング変調器の簡素化を図ることにします。具体的には、図7に示したようにトランスを取り除きます。ここでは、ADALM2000を使用し、搬送波信号と変調信号の和と差に相当する信号を生成します。それらの信号を、値の小さい2つの入力抵抗R1、R2を介してダイオード・リングの相対する接続点に供給します。この構成により、入力トランスが不要になります。出力信号は、値の大きい2つの出力抵抗R3、R4の両端で測定することができます。つまり、これらの抵抗が出力トランスの代わりになります。
ハードウェアの設定
上述したように、図7の簡素化したダイオード・リング変調器に対しては、ADALM2000のAWGを使用して信号を入力します。一方の接続点には搬送波信号と変調信号の和を印加し、もう一方の接続点には両信号の差を印加するということです。ブレッド・ボードにおいて、W1をR1の一端に、W2をR2の一端に接続します(図8)。オシロスコープのチャンネル1(1+)は、D1、D3、R4の接続点に接続してください。もう一方(1-)は、D2、D4、R3の接続点に接続します。最後に、R3とR4の間のノードをグラウンドに接続しましょう。
手順
この実習では、fc = 3sin(10kt)で表される搬送波信号と、fm =0.5sin(1kt)で表される変調信号を使用します。これら2つの信号は乗算され、出力信号はその積になります。出力信号には、上側波帯の周波数成分fusfと下側波帯の周波数成分flsfが含まれます。これらの定義は以下のようになります。
fusf = fc + fm
flsf = fc – fm
ここで、fcは搬送波信号の周波数、fmは変調信号の周波数です。
簡素化したダイオード・リング変調器を用いる実習では、側波帯の信号を直接入力します。搬送波信号と変調信号に注目すると、上側波帯はf(t) = 3sin(10kt) + 0.5sin(1kt)、下側波帯はf(t) =3sin(10kt) - 0.5sin(1kt)となります。
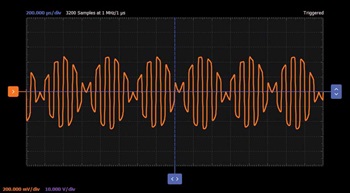
そこで、AWGのW1の周波数を1kHzとして、f(t) = (3×sin(10×t)) + (0.5×sin(t))という式を設定します。一方、W2の周波数も同じく1kHzとして、f(t) = (3×sin(10×t)) - (0.5×sin(t))という式を設定します。オシロスコープについては、水平軸を200マイクロ秒/div、垂直軸を500mV/divに設定してください。その状態でAWGとオシロスコープの機能を起動して波形を観測しましょう。すると、図9に示すような結果が得られるはずです。
問題1
図7の回路の抵抗値を変更するとどのような結果になるか確認してください。まずはR1とR2の値を1kΩに変更します。そうすると、出力信号の振幅はどのようになりますか。次に、R1とR2の値を元に戻した上でR3とR4の値を1kΩに変更します。その場合、出力信号の波形はどのようになりますか。
答えはStudentZoneで確認できます。