はじめに

近年ではいままでになく、回路設計・仕様がどんどんハイスピード化しています。デジタル回路とすれば、たとえばシリアルATA, IEEE-1394, USB 3.0, PCI Express, JESD204Bなどが例として挙げられるでしょう。そのため、これまでは”Black Magic”とされてきた高周波回路設計に関わる回路設計技法が、どんどん一般的な電子回路設計にも活用されてきています。

そのうちの主たるものが「伝送線路」と「特性インピーダンス」そして「Sパラメータ」といえるのではないでしょうか。

古くは、デジタル回路は「単に接続すれば動く」といわれていました。しかし近年ではとくに、ハイスピード・デジタル回路において、伝送線路と特性インピーダンスの考えを活用しないと設計できなくなってきています（トラブルが生じることになります）。

今回の技術ノートでは、Black Magicのうち「伝送線路」と「特性インピーダンス」について考えていきます。ちなみにBlack Magicなどと呼ばれてはいますが、結局は電子回路です。従来は無視してきたひとつひとつの要素を、想定内の要素として取り込んでいけば、それは普通の回路設計となんら変わらない、「別にMagicなんてモノではない」のだと気がつきます。

ハイスピード時代に多くの回路設計で注意すべきことは

ここで必要なことは、

◎  プリント基板上やケーブル内の電圧や電流の動きを「波動」として考えること
◎  パターンや導体を伝送線路として考え、また特性インピーダンスを考慮すること

今回の技術ノートはこんな話しをしていきたいと思います。それによって、「謎だ！」という人の多い、Sパラメータの入り口（反射係数の考え方）まで進んでみたいと思います。

現代のプリント基板は伝送線路で考える

「伝送線路」という用語を聞くと、「一体それはなに？」とか「自分には関係ない」とか思われる方もいるかと思います。しかし取り扱う信号が高速化してきている昨今では、プリント基板上のパターンを「伝送線路」として考える必要がでてきます（図1）。プリント基板のパターンは、電気信号を送端（ICの出力）から受端（ICの入力）に伝える媒体です。アナログ・ディジタルを問わず、パターン上を伝わる信号の変動の速さと信号が伝わる速度との関係が、パターン長を意識すべき、つまり信号が伝わっていく様子を意識すべきあたりになると、「伝送線路として考える」必要がでてくることになります。

なお伝送線路を信号が伝わる速度のことを、伝搬速度とか位相速度といいます。この技術ノートでは「位相速度」を用います。位相速度は以降に式(3)で示します。

この伝送線路、つまりプリント基板のパターンは図2のようにモデル化することができ、

◎ パターン自体（長さ）はインダクタ（インダクタンス）
◎ パターンとグラウンド間（近接）がコンデンサ（容量）

となります。このように全長にわたってインダクタンスや容量が存在しているものを「分布定数回路」と呼びます。ここでは伝送線路（パターン）なので「分布定数線路」とも呼ばれます。

図1. プリント基板のパターンは伝送線路

図2. 伝送線路（プリント基板のパターン）は
インダクタンスと容量で分布定数回路としてモデル化できる

 
図3. 電気信号は伝送線路を波動として伝わっていく
（ここでは10mの同軸ケーブルを伝送線路としている）

 
図4. 伝送線路としての10mの同軸ケーブルを
50MHz実効値10Vの電圧の波動が伝わっていくようす

 
伝送線路を特徴づける単位長インダクタンス／単位長容量

伝送線路／分布定数線路は、単位長あたりのインダクタンスL_U [H/m]、容量C_U [F/m]で考えます。同軸ケーブルも伝送線路であり、一般的な50Ωの同軸ケーブル（5D-2V）ではL_U = 250nH/m、C_U = 100pF/mになっています。

プリント基板上で正しく伝送線路を実現するにも、パターン全長にわたって、この単位長インダクタンスと単位長容量が一定である必要があります。つまり物理的形状が長手方向で変化しない必要性があります。

同軸ケーブルもプリント基板のパターンも「伝送線路」ですが、この技術ノートでは一括して「伝送線路」という用語で統一して説明していきます。

伝送線路を電圧と電流は波動として伝わっていく

電気信号（電圧V [V]と電流I [A]）は伝送線路中を「波動」として、位相速度で伝わっていきます。ここでは伝送線路の例として、図3のような10mの同軸ケーブルを考えてみます。

この伝送線路としての10mの同軸ケーブルを、実効値10Vの電圧の波動が伝わっていくようすを図4に示します。グラフの横軸は同軸ケーブル上の位置（観測点）です。点線／破線／実線として1nsごとのスナップ・ショットで、電圧分布の時間変動をプロットしてみました。同軸ケーブルの位相速度は光速の66.7%、2×108m/sになります。

このように電圧が「波動」として伝わっていきます。実際は電圧変化により、分布定数回路の各部で「LC過渡現象」が生じて、電圧と電流が変化し、その過渡現象が伝搬していくことになります。電磁気学的には電圧の波はスカラー量として圧力波のイメージ、電流の波はベクトル量として密度波になります。

伝送線路を伝わる電圧と電流の相互関係が特性インピーダンス

波動として（位相速度で）伝わっていく電圧V [V]と電流I [A]は、伝送線路の中では一定の比率になります。この相互関係／比率が特性インピーダンスZ₀ [Ω]で

単位は「オーム（Ω）」です。伝送線路の中にZ0という大きさの抵抗があるわけではありません。L_UとC_Uから決まることになるわけですね。なおプリント基板での伝送線路である「マイクロストリップ・ライン」は、図5のような

• パターン幅 W
• 基板絶縁体の高さ H
• 絶縁体の比誘電率 ε_r
• パターンの銅箔厚 t

という物理的形状から

として特性インピーダンスZ₀が決まります。ここに入れる数値の単位は「比」なので、なんでもかまいません。この式はアナログ・デバイセズのTutorial MT-094 [1] から抜粋したものです。原典は [2] のようです。原典の筆者Dr. Eric Bogatinは、Dr. Howard Johnsonと並ぶ、シグナル・インテグリティの大家です。

しかしさらに[2]にも原典があり（笑）、IPC-D-317A Design Guidelines for Electronic Packaging Utilizing High-Speed Techniques [3] から引用されているようです。IPCはプリント基板のご本尊という感じ団体で、現在はAssociation Connecting Electronics Industries; プリント基板／電子機器製造サービス産業協会という名前ですが、もともとは、Institute for Printed Circuits（IPC）と名乗っていました。このIPC-D-317A  [3]は古くに規定された技術資料のようですが、新しく発行されたIPC-2141A Design Guide for High-Speed Controlled Impedance Circuit Boards [4]では、より精密な特性インピーダンスの式 が規定されています。[3]は[4]の簡略式のようです。

それでも[4]で規定されているマイクロストリップ・ラインの特性インピーダンスの式は、超古典となっているWheelerの論文 [5] が参照されています…。「温故知新」という感じでしょうか（笑）。ところでこれらの式は「近似式」であり、その他にもいろいろ提案されています。

とはいえ手計算で求めるのも面倒なので、実際の現場的には、図6のようなツール [6] を用いて計算することが、現代の設計手法といえるでしょう。

 
図5. マイクロストリップ・ラインは物理的形状で 特性インピーダンスが決まる

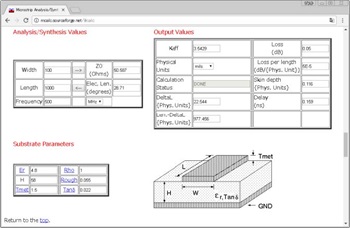
 図6. マイクロストリップ・ラインの特性インピーダンス 計算ツールの例
Microstrip Analysis/Synthesis Calculator [6]

 
信号が伝搬する速度（位相速度）

伝送線路の位相速度V_pも、L_UとC_Uから決まり

となります。単位は[m/s]です。同軸ケーブルの単位長値を代入してみると、V_p = 2×108 m/sとなり、光速の3×108 m/sの66.7 %ということが分かります。つまり同軸ケーブルの中を信号が伝搬する速度は、光速よりも遅いことになります。プリント基板上のパターンでも同じしくみになります（大体光速の50 %～60 %程度）。このプリント基板上の位相速度については、次の技術ノートTNJ-040であらためて説明します。

手持ちのプリント基板設計のスライドでも…

私がよく依頼される、プリント基板設計に関する技術講義でも実は似たようなスライドがあります（図7）。実際これは、ここまで説明してきた、「伝送線路の中を電気信号が波動として、位相速度で伝わる（伝搬する）」ことを、暗に説明しているものなのでした。

とくにこのスライドに関する重要なポイントとしては、グラウンド・プレーンとなる面にも、信号パターンに電流が流れたのにあわせて（まるで電流が誘起するように）一緒に電流が流れ始め、それが負荷端側に伝わっていくということです。

ハイスピード信号（高周波信号）を取り扱うプリント基板では、「パターンは伝送線路である」ということを意識して、設計する必要があるということでもあります。

ネット上でみかける「電球が点灯する順番」という質問も…

このように「電気信号が波動として伝送線路を伝わっていくのだ」と考えれば、たとえば2015年のアナログ技術セミナーでのクイズ、図8の答えはすぐに分かるはずです（答えは次回の技術ノートTNJ-040で実験により解説します）。

Googleで「電球が点灯する順番」とサーチすると、同様な疑問に関するたくさんのQ and Aページが現れ、それぞれで多数かつ熱心なディスカッションがなされています。なかには量子力学／仮想光子／素粒子論などを持ち出して議論しているページ[7]もありますね。伝送線路の振る舞いが「量子力学／仮想光子／素粒子論」だなんて話しになってくると、私も手も足もでません（笑）。

これは実験してみれば答えは明白です。その結果がゆるぎない答えになるわけですから。そこで次の技術ノートTNJ-040では実際にツイストペア・ケーブルを使って検証してみます（笑）。実は「電球が点灯する順番」の実験をしたいがために、この技術ノートTNJ-039が、その…、マエフリであったりするわけで…（笑）。TNJ-040を乞うご期待ください！

負荷端で信号が反射する

電圧と電流が波動として伝搬する比率が特性インピーダンスです。ところで図3では、特性インピーダンス50Ωの同軸ケーブルを伝送線路として考えました。ここで負荷抵抗としてR_L = 50Ωが接続されています（ここを「負荷端」とします）。

電圧と電流が淀みなく負荷抵抗に吸い込まれていく必要がある

伝送線路は「電流のみ／電圧のみ」を伝えることができません。「電圧と電流が必ずセット」となって、伝わっていくことを考える必要があります。負荷端でも「電圧と電流が必ずセット」となって、淀みなく負荷抵抗に吸い込まれていく必要があります。

特性インピーダンスZ₀の伝送線路中での、電圧Vと電流Iの関係は式(1)のとおりですが、ここで負荷端にZ₀に等しい抵抗R_Lを接続すれば

となり、負荷端で電圧Vと電流Iの波動は淀むことなく、負荷回路側に吸い込まれていくことになります。見方を変えれば、この負荷端は「伝送線路がさらに従属接続されているのと同じ条件」になっているわけです。これは有限長の伝送線路で非常に重要な概念です。

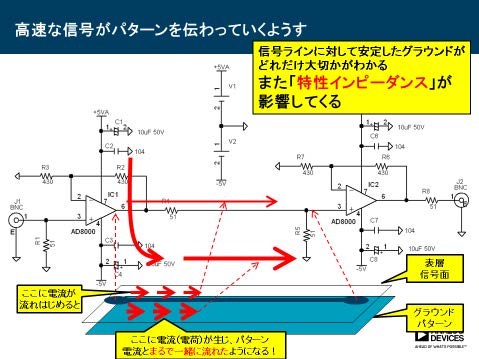
図7. 「伝送線路の中を電気信号が波動として位相速度で伝わる（伝搬する）」
ことを暗に説明している

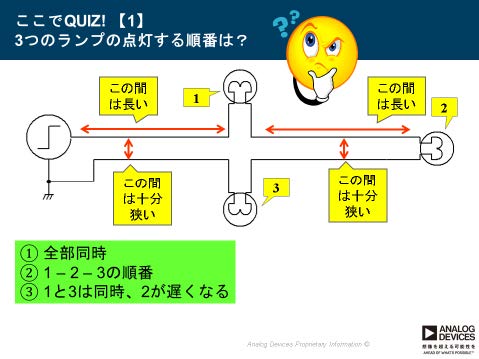
図8. 電気信号が波動として伝送線路を伝わっていくのだと考えれば
この答えはすぐに分かる

図9. 反射係数の概念を直流回路で考える

負荷抵抗が特性インピーダンスと等しくないと電圧／電流が反射する

この電圧Vと電流Iの関係が負荷端で維持できない場合はどうなるでしょうか。これは

という状態です。このとき負荷端で、電圧Vと電流Iが「淀む」ことになります。電気信号が淀むとは「電圧Vと電流Iが負荷端で反射する」という振る舞いになります。このときの反射する率を反射係数𝜞といい

という式で表します…。といってもこの式(6)は書籍などでよく見かけるものでしょう。しかし、なぜこの式が成り立つのでしょうか。それをもう少し考えてみましょう。

反射係数の概念は直流回路で考えられる

図9に反射係数の概念を、非常に単純な直流回路で考えてみたものを示します。別に難しいものではないことが分かります。

図9の抵抗Z₀の右側が伝送線路の負荷端で、抵抗R_Lが接続されているとします。Z₀が特性インピーダンスに相当します。いまR_L = Z₀であれば、V_RLは1V（V_S/2）になります。これが淀みなく負荷抵抗に吸い込まれていく条件になるわけで、このとき伝送線路を信号源から負荷端に伝わっていく波（進行波）V_Fは、V_RLと等しく

いっぽう式(5)の条件でV_RLは

ですが、これが進行波V_Fと反射する波（反射波）V_Rの合計として

これを変形して、反射波V_Rを求めてみると

このV_Fは式(7)のとおりなので、右辺は

ここにまた式(7)を使うと

反射係数𝜞はV_RとV_Fの比なので

こんな単純な直流回路で、反射係数の概念を見事に求めることができます。実際の交流（高周波）回路では、RLを複素数（インピーンダンス）にして、複素数計算として位相もふくめて考えれば良いことになります。

シミュレーションで確認してみる

図10はADIsimPEの伝送線路モデルを用いたシミュレーション回路です。伝送線路の伝搬時間は5nsとしてあり、位相速度v_p = 2×108 m/sの同軸ケーブルだとすれば、1m長に相当します（ここではこの長さはあまり関係ありませんが）。

信号源変化は0V ～ 5V、信号源抵抗と伝送線路の特性インピーダンスは50Ω、負荷抵抗は220Ωにしてあります。

シミュレーション結果を図11に示します。進行波の大きさは信号源電圧の半分ですから、2.5Vです。それが最初の5nsの間に観測されています。負荷端での反射係数は、式(6)から0.63と計算されます。

進行波が負荷端に到達すると、2.5V × 0.63 = 1.575Vの電圧が反射します。この反射波は、進行波の電圧2.5Vに足された（重畳した）かたちになりますので、伝送線路上では4.075Vが観測されることになります。図11のシミュレーション結果では、反射波が重畳した電圧値をマーカで測定していますが、4.074Vになっていることが分かります。

信号源側は50Ωの信号源抵抗があるので再反射が生じない

ここで反射波が信号源に到達したときに、どのように振舞うかということを考える必要があります。

ここまでの文脈では、信号源に到達した電気信号を「反射波」として説明してきました。しかしよくよく考えてみると、この反射波は、「伝送線路という媒体の中を伝搬する信号」には変わりないわけで、「モノ」自体は進行波と同じです。伝送線路を「右から左に」伝搬しても「左から右に」伝搬しても、それはなんら変わらず、当然ながら同じなわけです。

 
図10. 反射係数を確認するシミュレーション回路

つまり反射波が信号源に到達したときも、負荷端で生じていた反射係数のしくみを、まったく同じように適用することができるわけです。

信号源となる電圧源は「抵抗がゼロ」です。そこに信号源抵抗50Ωが接続されているわけですから、反射波からすれば、信号源抵抗は「負荷端の負荷抵抗」と全く同じになります。ここで

Z₀=R_S

ですから反射係数 𝜞 は

となり、信号源に到達した反射波の「再反射」は生じないことになります。それにより、図11の結果となるのでした。

このしくみが「送端終端」というテクニック

このように信号源抵抗を特性インピーダンスに整合させ、信号源に到達した反射波の「再反射」を生じさせないテクニックを、「送端終端」と呼びます。

送端終端のしくみはCMOSデジタル信号伝送でも活用できる

このしくみを利用すると、3.3Vや5VのCMOS信号も、信号品質を維持して（余計な反射を生じさせずに）負荷端に伝送させることができます。

図3のような信号伝送では、信号源／負荷端それぞれに伝送線路の特性インピーダンスに整合した抵抗が接続されています。これでは5Vで送出するCMOSデジタル信号は、半分の2.5Vになってしまい、負荷端（レシーバ側）では正しくレベルを検出できません。

しかしここで、図10や図11で示した送端終端のテクニックを用いることを考えてみましょう。図10の負荷抵抗R2が無限大だとすれば、ここで一旦反射は生じますが、送端終端により、（図11と全く同じように）信号源に到達した反射波の「再反射」は生じません。負荷端（レシーバ側）で信号源からの再反射は（これも図11と全く同じように）観測されず、負荷端の信号波形は暴れることなく、安定した信号伝送が実現できることになるわけです。

送端終端しない従来のCMOSデジタル伝送の場合は

それでは従来のCMOSデジタル伝送（終端抵抗は考えていない）のようすをシミュレーションでみてみましょう。図10の信号源抵抗R1をCMOSドライバ出力抵抗相当として5Ω、負荷抵抗R2をCMOSレシーバ入力抵抗相当として1MΩに設定します。

結果を図12に示します。伝送線路の信号源／負荷端それぞれ、そしてとくに負荷端（レシーバ側）が大きく暴れていることが分かります。これは伝送線路のどちらの端でも反射が生じている状態で、これを「多重反射」と呼びます。CMOSレシーバ側に相当する負荷端側は、CMOSスレッショルドである2.5Vを割り込んでおり、これではまともな信号伝送ができません。

これを図11のように「送端終端」することで、（実際の波形は示しませんが）負荷端側の信号の暴れをなくすことができるわけです。送端終端のテクニックは、このようにCMOSデジタル信号伝送でも活用できるのです。

なぜ従来のCMOSデジタル回路で送端終端がなくても動作していたのか

「これまで長くCMOSデジタル回路を設計してきたが、送端終端なんてしていないし、ちゃんと動いていたぞ」という方が（私も含めて…）多数かと思います。

このような波形が観測されなかったのは、① CMOSデジタル信号波形の立ち上がり時間が、伝送線路（パターン）の往復時間（つまり反射の生じる時間）に対してゆっくりだったこと、② 伝送線路／パターン自体の距離が十分に短かったこと、が理由です。

つまり、物理現象としては多重反射が生じていたわけですが、ただそれが見えていなかっただけなのです。

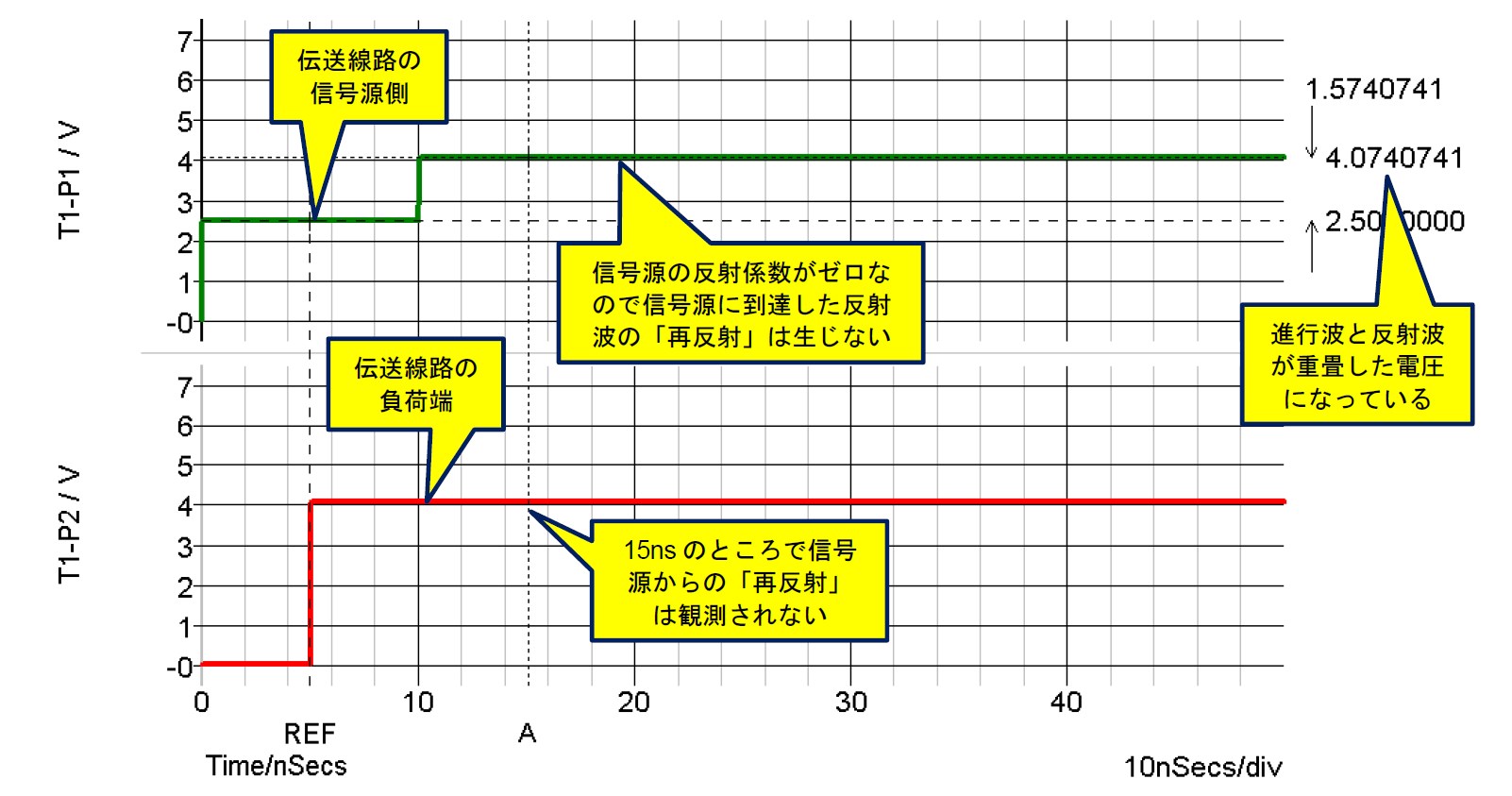
図11. 図10のシミュレーション結果

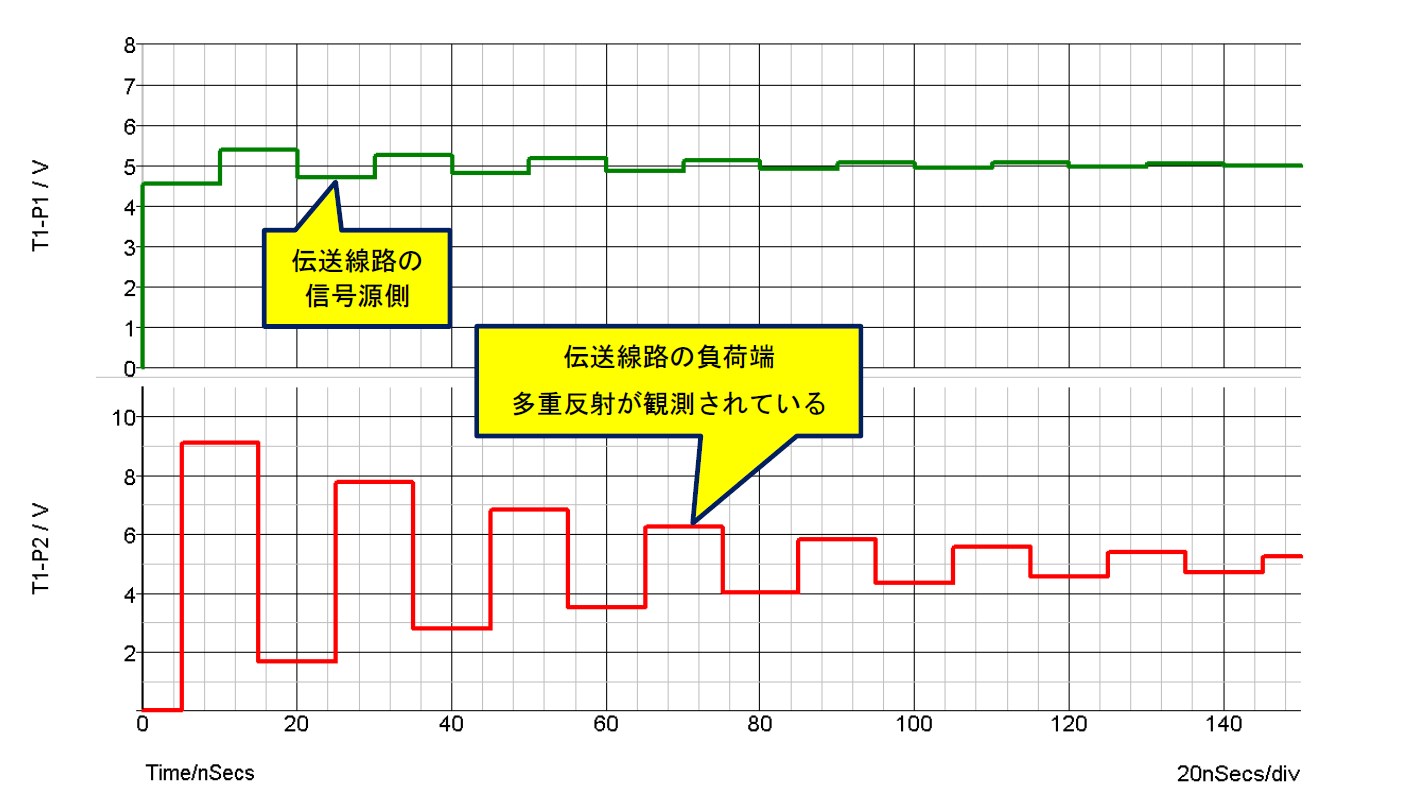
図12. 図10の回路で信号源抵抗R1 = 5Ω、
負荷抵抗R2 = 1MΩにしたときのシミュレーション結果
多重反射が観測されており、とくに負荷端（CMOSレシーバ側）は
スレッショルド電圧を割っている！

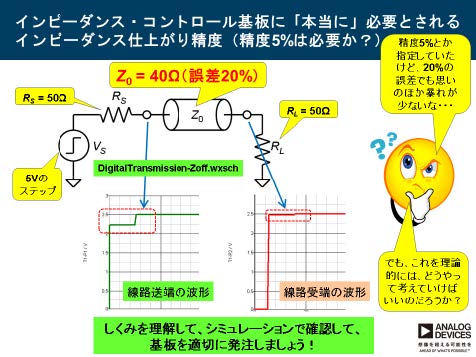
図13. 2015年のアナログ技術セミナーで示したスライド

送端終端はダンピング抵抗と同じではないか？

「送端終端って、なんだかダンピング抵抗と同じ感じがするな？」と感じる方もいらっしゃるのではないでしょうか。しかしこのふたつは、それぞれ異なる振る舞いなのです。ダンピング抵抗は、回路を集中定数LC回路網として扱い、そのQ値（Quality Factor）を低下させるように作用するものです。

一方で送端終端は、信号を「波動」として考えたとき、反射を抑えるように働くものです。そのため違う動作に対して抵抗を用いていることになります。

なおCMOSデジタル回路のプリント基板設計で、安易に「ダンピング抵抗と送端終端の両方に効くように、抵抗を挿入しておきたい」とすれば、CMOSドライバ側に数10Ωの抵抗を挿入しておけば、一つの抵抗で最大限の効果を発揮させることができます。

反射係数のわりには波形変化が少ないぞ？

2015年の「アナログ技術セミナー」で、本技術ノートに関連する話題をお話ししました。

そこでは、伝送線路と特性インピーダンス…というストーリでお話していきました。適切な特性インピーダンスの伝送線路をプリント基板上で実現するために、「インピーダンス・コントロール基板」という話題をご提供しました。

基板製造を考慮して適切な仕上がり精度指示という提案で

しかしプリント基板を製造するうえでは、パターンのオーバ・エッチング／アンダ・エッチングにより、目的のパターン幅ぴったりに製造することは非常に難しいです。

一方でインピーダンス・コントロール基板として製造を依頼する場合に、どの程度の仕上がり精度指示をすればいいか、見当がつかない場合もあるのではないかと思います。もしかしたら「1%精度でお願いします」などと言ってしまうこともあるでしょう。

しかし精度を上げれば歩留まりが低下し、コストが上昇します。そのため適切な仕上がり精度で指示する必要があります。そこで「アナログ技術セミナー」では、図13のような提案をしました。「20%のインピーダンス誤差で波形がどうなるか」というものです。

シミュレーションした回路は、図14のように入出力終端抵抗が50Ω、線路の特性インピーダンスが40Ω（線路伝搬時間は5ns）で20%もずれており、ハイスピード・デジタル信号回路において、「インピーダンス・コントロール基板のインピーダンス精度をそれほどシビアに指定する必要はないのですよ」という話をしたかったものでした。

シミュレーションを用意した本人は、スライド作成時には「暴れは小さいよね（笑）」でスルーしていたのですが、終わったあとであらためて考えてみると「インピーダンス誤差が大きくても、負荷端の波形変化はたしかに小さい。しかし反射係数𝜞の大きさから考えて、波形変化は小さすぎないか」ということに気がつきました（汗）。

シミュレーション結果を精査してみる

図15はシミュレーションの結果です。反射係数を計算してみると、R_S=R_L=50Ω,  Z₀=40Ωから

図14. 提案でのシミュレーション回路（図10の回路で R1 = R2 = 50Ω、Z₀ = 40Ωとした）

で、反射波は進行波の11%になります。負荷端からはこの率で反射していることは違いありません。しかし図15の変化点を拡大した図16においては、変化量が30mVであり、1.2%程度しかありません。「確かにこれは不思議」です。

信号源側での注入量（進行波の大きさ）が異なるのだ

一方、信号源側もR_S≠Z_0になります。ここがミソで、これにより進行波V_Fの大きさが整合時と異なる（小さくなる）ことから、多重反射の暴れが小さくなっています。まず信号源側の等価モデルを考えると、進行波V_Fは

となります。図14の条件だと、整合時より進行波V_Fは若干低くなります。

つづいて負荷端を考えます。進行波V_Fが負荷端に到達した瞬間の、負荷端の端子電圧V_RLを図9の等価モデルで考えると

となり、0.493827 × 5V = 2.469135Vで、図16のシミュレーション結果とぴったり一致することが分かります。なお以降、多重反射を繰り返し（図15では変化は見えませんが）、最終的にV_RLは

に収束します。R_S, R_LとZ₀の大きさの相互関係が逆でも、同様に計算できます。結構ややこしく、かつ面白いものですね。

まとめ

今回の技術ノートでは「伝送線路」と「特性インピーダンス」そして「反射係数」についてお話しました。ハイスピードな信号は「波動」だと考えることがポイントです。

次回は、今回の技術ノートの理解を基礎として、ネットを騒がせている（？）「電球が点灯する順番」の実験を、ツイストペア・ケーブルを使って実際に検証してみましょう（笑）。

参考・引用文献

[1] Microstrip and Stripline Design, Tutorial, MT-094, Analog Devices.

[2] Eric Bogatin, Signal Integrity – Simplified, Prentice Hall. 邦訳は「エリック･ボガティン; 高速デジタル信号の伝送技術 シグナルインテグリティ入門, 丸善」

[3] Design Guidelines for Electronic Packaging Utilizing High-Speed Techniques, IPC-D-317A, 1995, The Institute for Interconnecting and Packaging Electronic Circuits.

[4] Design Guide for High-Speed Controlled Impedance Circuit Boards, Standard IPC-2141A, 2004, The Institute for Interconnection and Packaging Electronic Circuits.

[5] H. A. Wheeler; Transmission-Line Properties of a Strip on a Dielectric Sheet on a Plane, IEEE Transactions on Microwave Theory and Techniques, Col. MTT-25, Aug. 1977, pp. 631 - 647.

[6] Microstrip Analysis/Synthesis Calculator, http://mcalc.sourceforge. net/#calc （もしくはWcalc: http://wcalc.sourceforge.net/）

[7] 電球が点灯する順番, 質問！ITmedia, http://qa.itmedia.co.jp/qa615057.html

図15. 図14のシミュレーション結果（緑 = 信号源側、赤 = 負荷端側）

 

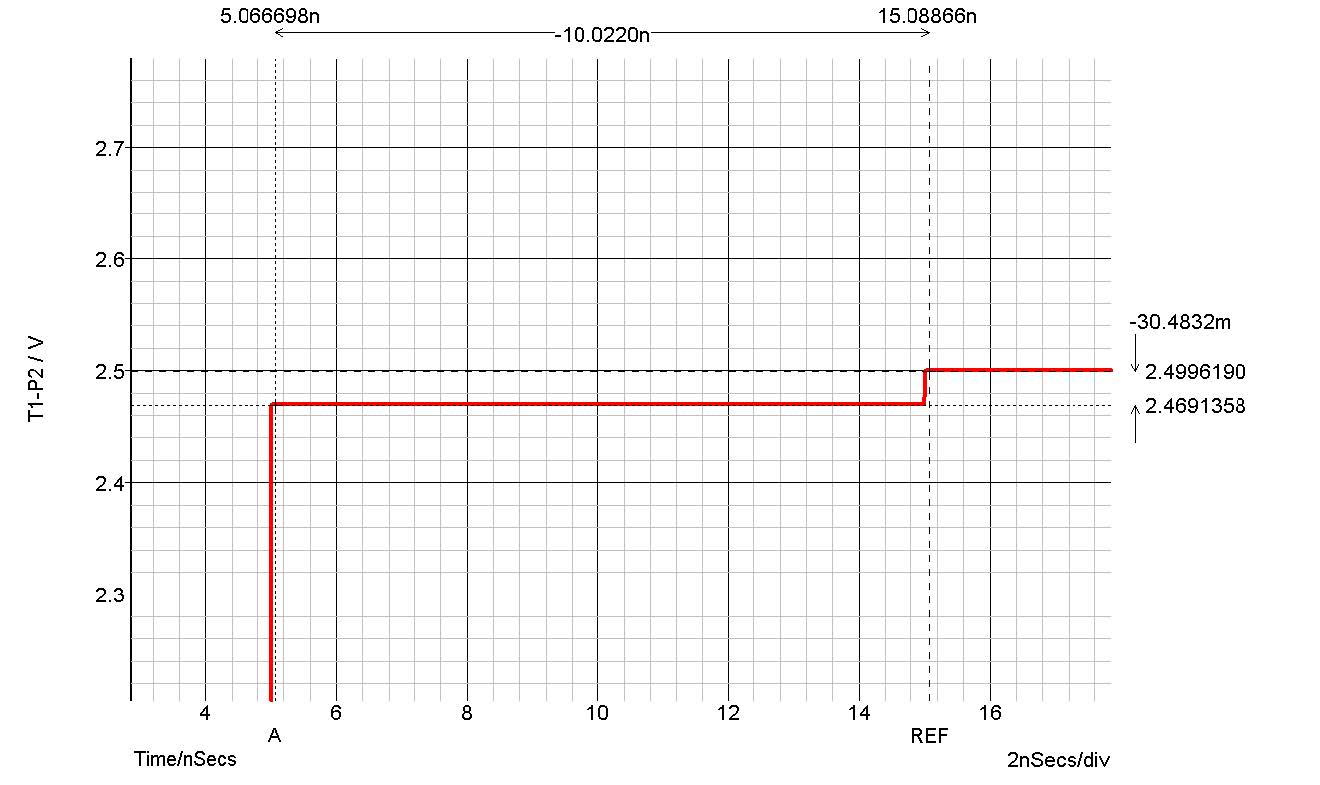
図16. シミュレーション結果の赤 = 負荷端側の波形変化点を拡大してみた