TNJ-028:トランスのM結合とはナニモノでどのように測るか 前編:
2017年3月6日公開
はじめに
どうでもいい話しですが「はかる」もいろんな漢字がありますね。「計る、図る、測る、諮る、謀る…」。日本語は難しいです。
さて、「トランス」。あまりなじみの無い方も多いかと思いますが、最近は電源回路だけではなく、差動信号などでの設計・応用もあります。そのためトランスも電源エンジニアだけのものではない、多くの方々に関係する話題といえるのではないでしょうか。実際問題としては(当然ながら)、「最近」というわけでもありませんね。
そのトランス。一次、二次の自己インダクタンスL1,L2、そして相互インダクタンスMはどうやってハカレばよいでしょうか。この(三部作の前編となる)技術ノートでは、それらをハカる方法の理論的な側面を説明し、そしてADIsimPEを用いて、シミュレーションで測定方法を検証してみたいと思います。
一つ前の技術ノートTNJ-027では、デジタル・アイソレータのトランスと100万Vのトランスをご紹介しましたが、次のこの技術ノートでも、続いて、同じく「トランス」です(笑)。

図1. トロイダル・コア活用百科
名著中の名著と呼ばれる・・・
図1は「名著中の名著」とも呼ばれる「トロイダル・コア活用百科(CQ出版社)です。絶版になりましたが、現在は「改定新版」が別に発売されています。
1983年初版とのことですが、私は一体いつごろに買ったことやら…。キレイな表紙をお見せするのが格好良い記事(技術ノート)でしょうが、このようなぼろぼろになった書籍をお見せするのもエンジニアとしてのリアル感があり、「一興」だともいえるでしょう。「ぼろぼろ」のとおり、かなりのところを読んで参考にさせてもらいました。それでもまだ読みきれていないところがあるというのも面白い話です(ページ数もかなりあるため)。
相互インダクタンスMとは?
まずは自己インダクタンスLから…
自己インダクタンスL(単位はヘンリー[H])は、図2のように、電流Iの変化に対してインダクタの両端でどれほどの電圧VEMF(起電力; electromotive force, EMF)が生じるかを表す数値です。式で表してみると

dI(t)/dtは電流Iの時間変化です。この式は「電圧降下」として考える極性で起電力VEMFを表記していますので、符号はプラスですが、本来の「起電力」として考えるのであれば(電圧源の電圧と電流の極性で考えるのであれば)符号はマイナスになります。

図2. インダクタに流れる電流変化で起電力が生じるが
この生じる量の係数が自己インダクタンス
I(t)は過渡変化であればいろんな形になるでしょうが、一般的には定常状態として
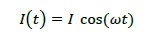
ここでωは角周波数(ω=2πf)で、このような波形を加える(考える)ことが一般的でしょう。コサインが微分されるわけですから、
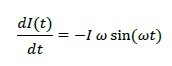
となり、これを最初に式に代入してみると
![]()
となり、-sin(ωt)はcos(ωt)に対して90度位相が進んでいますから、-sin(ωt)→j〔=exp(jπ/2)〕としてみると
![]()
となり、よく見る式に変形することができます。
つづいて相互インダクタンスMとはナニモノ…
相互インダクタンスの記号Mは、英語の「Mutual」という単語から来ています。
「Mutualといえば…」というわけではありませんが、弊社はお客様と秘密保持契約(NDA; Non Dislosure Agreement)を締結させていただき、新規開発品のご紹介ですとか、共同開発などを行っています。アナログ・デバイセズでのこのNDAのタイトルが、
MUTUAL NONDISCLOSURE AGREEMENT
として、「相互に」という意味で「Mutual」という単語が使われています。相互インダクタンスも同じイメージです。
さて、自己インダクタンスは「インダクタ自ら(自己)」に流れる電流Iの変化に対して生じる電圧VEMFなわけですが、相互インダクタンスM(単位は自己インダクタンスと同じく、ヘンリー[H])は、図3のように二つの電線(もしくはインダクタ/コイル/トランスの巻線)の間で生じる相互作用で、一本の電線に電流Iが流れていると、もう一方の電線の両端に生じる電圧VEMFを
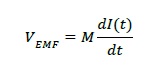
として表せるものです。一般的な定常状態として考えると、
![]()
となります。「電流によって起電力が生じるが、その度合いが、自分ならL、他人ならM」と考えてしまえばよいでしょう。
ということで定義は分かりましたが、自己インダクタンスと相互インダクタンスの間には「結合係数 k」という関係があります。このあたりを、この技術ノートでは解きほどいていきたいと思います(…この歳で今更気づいたことですが、「とき=解き」で、また「ほどく=解く」ですが、「ときほどく=解き解く」とはほとんど書かないですね…)。

図3. 一本の電線に流れる電流変化で、
もう一方の電線に起電力が生じる係数が相互インダクタンス
自己インダクタンスと相互インダクタンスとの関係を解きほどく
図4はトランスを解体したものです。トランスは一次側に電圧V1を加えれば二次側に電圧V2が生じるというものです。一次側、二次側ともども「マキモノ(巻き物)」ですから、自己インダクタンスL1,L2があろうこと、また相互に結合しているので相互インダクタンスMもあろうことが想像できるでしょう。
トランスの二次側に電圧V2が生じるしくみは、相互インダクタンスがなければ成り立たないことも気がつきます。図3で示したように「相互インダクタンスは二つの電線(もしくはインダクタ/コイル/トランスの巻線)間の相互作用で、一本の電線に流れる電流Iの変化により、もう一方の電線の両端に電圧VEMFが生じる」というものなわけですから。

図4. トランス。一次側巻線と二次側巻線が同じコアに巻きつけられている。
電線のマキモノなので自己インダクタンスと相互インダクタンスそれぞれがありそうだ
このトランスのL1,L2,Mを、等価回路として表したものが図5になります。これは一般的に、よく用いられるトランスの等価回路です。相互インダクタンスMは

として表されます。ここでkは一次・二次間の結合度で、「結合係数」といいます。式変形してみると、

となることが分かります。
なぜ結合係数なるものが必要なのか(生じるのか)
それではなぜ、このような一次・二次間の結合度や結合係数を定義する必要があるのでしょうか。
図6に示すように、トランスなどでは一次巻線で生じた磁束がすべて二次巻線の領域内を通り抜けず、漏れとなる磁束の量ができてしまいます。ファラデーの電磁誘導の法則のとおり、コイルに誘起する電圧(起電力)は、そのコイルのループの中を通る変動磁界量(より電磁気学的には「鎖交磁束」と呼びます)に比例します。一次巻線で生じた磁束の一部が、このループ内を通らないのであれば、それは二次巻線の起電力として影響を与えないことになります。
これが「漏れ磁束」で、図5においてはL1-M, L2-Mで表されます。「漏れ磁束」を考慮するため、結合係数が必要なのです。
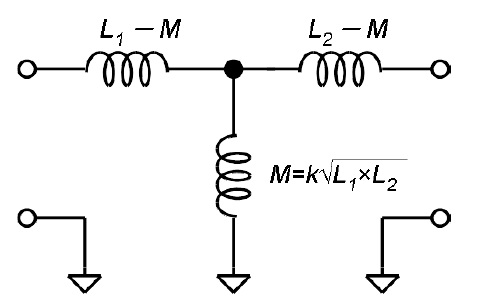
図5. 結合係数もふくめたトランスの等価モデル

図6. トランスでの漏れ磁束により結合係数が1以下になる
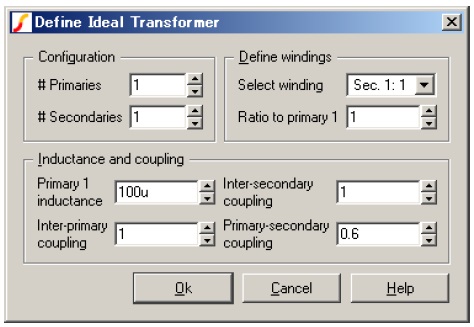
図7. シミュレーションでみてみるトランスの回路パラメータ
シミュレーションで答えを得る前準備(シミュレータでの各種定義)
それではアナログ・デバイセズのSPICEシミュレータADIsimPEを使ってシミュレーションをしてみましょう。図7はシミュレーションでのトランスのパラメータです。パラメータのなかみを少し詳しく説明しておきましょう。
Configurationの# Primaries, # Secondariesは一次側(Primaly)と二次側(Secondary)に、それぞれある巻線の数(#はNumberという意味があります)です。ここではそれぞれ1巻線ずつなので、1になっています。
その右のDefine windingsは、値を入力したい巻線を選択します。Select windingがSec. 1:1になっていますが、ここはプルダウンで選ぶことができます。つづいて選択された巻線(図7の表示状態では二次側の巻線)の巻数比をRatio to primary 1として、一次巻線の1番目の巻線数との比で設定します。このシミュレーションの条件では、一次側と二次側は同じインダクタンス(巻数)なので1としてあります。
これまでの説明自体もちょっとややこしいですが、図7の設定ではそれぞれ1巻線ずつなので、実際はあまり気にしなくてもよいでしょう。
下のInductance and couplingのPrimary 1 inductanceで、一次巻線の1番目(このシミュレーションの設定では1巻線しか無い)のインダクタンスを設定します。ここを100μHに設定することで、またさきのRatio to primary 1(巻数比)を1に設定することで、一次の自己インダクタンスL1と、二次の自己インダクタンスL2をそれぞれ100μHに設定することができます。なお全ての巻線のインダクタンスは、インダクタンスL1からの相対値(巻数比)になります。
Inter-primary couplingとInter-secondary couplingは(複数巻線を設定したときの)一次巻線内、二次巻線内での結合係数を示しています。繰り返しますが、それぞれ1巻線ずつなので1にしておけば、あまり気にしなくてもよいでしょう。
Primary-secondary couplingがこの技術ノートでのキモの「結合係数」です。ここを0.6とすることで、結合係数 k = 0.6としてみました。
シミュレーションでは、「L1,L2は定義されているが、(0.6と設定した)結合係数 kが未知」だとして、相互インダクタンスMを求めてみたいと思います。

実際にシミュレーションしてみる
自己インダクタンスをシミュレーションで求めてみる
まずシミュレーションにより、図7で設定したトランスの自己インダクタンスを求めてみます。
図8は実際のシミュレーション回路です。トランスの二次側は開放にします。それでも片側をグラウンドに落としていますが、これはADIsimPEでシミュレーションを行う際に、
Errors found during the run. Simulation aborted
*** ERROR *** Singular matrix
This may be due to a floating node or a loop of voltage sources and/or inductors.
となるエラーを抑制するためです。二次側が開放でフロートのままだと、DC動作点を決められないということですね。
つづいて具体的なシミュレーションから計算への考え方です。トランスの一次、二次に流れる電流をI1, I2とすれば、一次に誘起する電圧V1は
![]()
となります。二次側が開放であるため I2 = 0であり、相互インダクタンスMにより誘起する電圧分はありません。こうすると、
![]()
が得られます。なおシミュレーションでは I1 = 1Aとしています。そうすればリアクタンスXLがそのまま電圧値V1として、
![]()
で得られることになります。
ACシミュレーションでシミュレーションしてみました。信号源を1Aとして周波数スイープさせ、トランスの端子電圧を求めてみます。図9のようにマーカでてみると、1MHzで628.319Vと答えが得られます。上記の式のとおり、得られた電圧値がそのままリアクタンスXLになることから、ω=2πf, f = 1MHzとすると、
![]()
とみごとにL1の大きさが得られることが分かります。



接続を変えてシミュレーションしてみる(その1)
次は相互インダクタンスMを求めてみるために、一次側と二次側を図10のように接続します。ここでは同じ電流量(1A)が一次巻線と二次巻線に流れます。
図11のようにマーカでみてみると、1MHzで2010.619Vと得られます。上記の式からω=2πf, f = 1MHzとすると、
と計算できます…。しかし一体これは何を見ているのでしょうか。

接続を変えてシミュレーションしてみる(その2)
つづいて一次側と二次側を図12のように接続します。先ほどとは電流の流れる向きが一次/二次間で逆になります。流れる電流量は一次巻線と二次巻線では同じ(1A)です。
図13のようにマーカでみてみると、1MHzで502.655Vと得られます。上記の式からω=2πf, f = 1MHzとすると、
![]()
と計算できます。接続する向きを変えるだけでインダクタンスが変わりますね。
これらが相互インダクタンスMの大きさを求めるための基本になります。
シミュレーション結果から相互インダクタンスを計算してみる
ここまでの、それも後半の二つのシミュレーションで、二つのインダクタンス値を求めてきました。

というものです。
トランスのそれぞれの巻線で誘起する電圧は

なわけですが、ここでは同じインダクタンスかつ同じ電流量なので、L1=L2=L,I1=I2=Iとすることができ、
![]()
と一般化できます。さらに図10と図12では、一次/二次が直列に接続されているので、図10のケースでは、
![]()
が得られ、図12のケースのように電流の向きを逆にして結線した場合では、
![]()
が得られます。これらを用いて計算してみると、まずそれぞれの値の引き算
![]()
から、M = 60μHが得られることになります。さらにそれぞれの値の足し算
![]()
から、L = 100μHが得られることになります。
結合係数がk = 0.6ですから

の式からM = 60μHというのも、つじつまがあっていますね。
ここではシミュレーションにより相互インダクタンスを求めてみましたが、実測でも同じように求められることもお分かりいただけるかと思います。これは三部作の後編(TNJ-030)で実際に実測してみたいと思います。
結合係数が高いケースでの漏れインダクタンスの簡易測定方法
結合係数が高いケースでの漏れインダクタンス(L1-M)もしくは(L2-M)の求め方をご紹介しておきます。一次/二次が同じインダクタンスの場合の簡易的な測定方法です。
二次側をショートすると、一次側からは一次側の漏れインダクタンス(L1-M)と、相互インダクタンスMと二次側の漏れインダクタンス(L2-M)の並列接続とで、
![]()
が見えることになります。ここで結合係数が高ければ、
![]()
となりますから、上記の式は
![]()
として簡略化することができます。一次/二次が同じインダクタンスなので、L1=L2であるため、二次側をショートして一次側からのインダクタンスLを測定して1/2することで、漏れインダクタンス量を、
![]()
として簡略的に求めることができます。
インダクタンスを簡易的に測定する方法
ところで実験でインダクタンスLを簡易的に求めるには、交流信号源から適当な大きさの抵抗Rを経由してLにつなぎ、そのときの交流信号源の電圧VSと周波数(角周波数ω)、Lの端子電圧VLから、

というかたちで式を立て、変形し、

とすればよいのです。といってもトランスの銅損や鉄損が見えてくる可能性も高いので、上記で得られた結果を鵜呑みにすることも注意が必要です。
まとめと関連する資料およびひきつづきの話題のご提供
トランスには相互インダクタンスというものが存在し、それが自己インダクタンスと「結合係数」でつながっていることをご説明しました。
またその相互インダクタンスと結合係数を求める方法についても、トランスを図10、図12のように接続することで測定により得られることが分かりました。
説明はシミュレーションにより行いましたが、実測でも同様に値が得られることになりますので、このアイディアは多岐に活用いただけるものかと思います。
インダクタンス測定に関する関連資料
関連資料をご紹介しましょう。
NF回路設計ブロックさんのウェブサイトです。ここに登録することで、郵送で「LCRメータを用いた電子部品の測定」という冊子を送ってもらえます!
アジレント・テクノロジーさんの「インピーダンス測定ハンドブック」という124ページの大作です。URLは古いまま(分社前)のものですが、技術資料のサイトとしてまだアクティブなようです。
ひきつづき中編・後編へつながる話題
この前編では理論的な面と、それを確認するためのシミュレーション結果についてご説明しました。以下は、この技術ノートの続きとなる、中編・後編に関する話題です。
この検討を行っていた前後で、とあるトレーニング用にUS資料(パワーポイント)の翻訳を始めたのですが、そこに見慣れない用語がありました。サーチしてみると、とあるアメリカの小さな会社のことでした。
なんと!そのサイトを見てみると、本当に偶然ですが、そこでローコストなLCメータを発売しており、$120 + $12(シッピング費用)だったので、面白そうなので買ってしまいました!なおキットなら$99です。キットで自作を楽しんでもいいのですが、キットを作る時間を取るならやるべきこともあり、完成品を購入してしまいました(汗)。とはいえ、なんとこのコストで1%精度なのでした…。
※
中編(TNJ-029)と後編(TNJ-030)では、このLCメータの購入の顛末、そしてそのノウハウや関連情報のご紹介、さらにこの前編でお話した相互インダクタンスと結合係数を求める方法について、このLCメータを用いて実際に測定してみたようすなどをご紹介していきたいと思います。
著者について
デジタル回路(FPGAやASIC)からアナログ、高周波回路まで多...






















