TNJ-005:ロー・ノイズOPアンプの性能をSPICEで最適化してみる
2013年11月1日 公開
はじめに
技術ノートTN-004JPでは、ノイズ・フリーな理想アンプを用いて抵抗から発生するサーマル(熱・ジョンソン)ノイズについて考えてみました。ここではこれを「ジョンソン・ノイズ」と呼ぶことにします。さてこの技術ノートでは、実際のロー・ノイズOPアンプ「AD797」を使ってノイズ特性の最適化をしてみましょう。
AD797は最新のデバイスではありませんが、今でもトップ・クラスのロー・ノイズ性能をもっているものです。
実際のOPアンプのノイズ・モデル
まずOPアンプのノイズ・モデルについて説明します。OPアンプは非反転入力(+)と反転入力(-)の2入力になっていますが、
- 電圧性ノイズは、+(もしくは-)の端子に直列に接続されている電圧源としてモデル化されます
- 電流性ノイズは、+と-のそれぞれの端子からグラウンドに並列に接続されている電流源としてモデル化されます
つまりモデル化されたノイズ源は、図1のように3つあり、
- 電圧性ノイズ
- 非反転入力(+)に流れる電流性ノイズ
- 反転入力(-)に流れる電流性ノイズ
になります。この1) ~ 3)はそれぞれ「非相間」の電圧/電流の変化であり、合成されたノイズ量は「電力の足し算, RSS; Root Sum Square」になります。

図1. OPアンプのノイズ・モデル
まず一般的な帰還抵抗を用いてみた
解析する回路、それも一番最初にやってみるものを図2に示します。
信号源抵抗R1はかなり小さい値(0.001Ω)にして、ジョンソン・ノイズが無視できるものとしてあります。
帰還抵抗R2, R3は一般的に使われる大きさを想定して、9kΩ、1kΩにしてあります。9kΩというのは現実の抵抗部品では非現実的(たとえばE24系列などという意味)ですが、利得を10倍にするために9kΩにしてあります。そういう意味ではシミュレーションは便利ですね。

図2. 最初にシミュレーションしてみる回路。帰還抵抗は一般的に使われる9kΩと1kΩ
AD797のノイズ性能
AD797のノイズ性能は、1kHzにおいて、
INPUT VOLTAGE NOISE 0.9 nV/√Hz typ (1.2 nV/√Hz max)
INPUT CURRENT NOISE 2.0 pA/√Hz typ
となっています。これが回路全体で相互にどのようにつながっているかを見て行きましょう。
NI Multisimでシミュレーションしてみる
図2の回路をNI Multisim Analog Devices Editonでシミュレーションした結果を図3と図4に示します。図4のノイズ量をみてください。増幅率が10倍ですから、V1に換算された入力等価ノイズ量inoise_spectrumとonoise_spectrumは(V2なので)100倍の関係になっています。

ここでは信号源抵抗はほぼゼロ(R1 = 0.001Ω)としています。つまりノイズもゼロと言えるはずです。しかし図4のinoise_spectrum = 1.9732E-15をルートして、入力換算ノイズ電圧量としてみてみると、V = 4.4nV/√Hzになっています。結構大きな量のノイズです。
支配的なノイズ源はAD797ではなくR3!
図4から、どれが支配的なノイズ源なのかと見てみると、R3であることがわかりますね。実際には
- このR3からのジョンソン・ノイズに対して(R2もそうだが小さい量)
- OPアンプの電圧性ノイズと、
- 抵抗R2とR3を並列接続したものにOPアンプAD797の反転入力の電流性ノイズがV = IRで電圧量となり、
それらがRSSで足し算されたかたちで、さらに増幅されて出力に現れてきます。
しかしAD797の電圧性ノイズは0.9nV/√Hzなんです!…。それと比べて、①のようなところから現れるノイズ、それらの合計で4.4nV/√Hzというのは、結構大きいですね…。
これから判ることは、ロー・ノイズ設計では「使用する抵抗値などを良く考えて設計しないと目的の性能が出ない」ということですね。

図 4. マーカ・リードアウト
帰還抵抗を小さくしてみた
ここまでで、R2とR3(実際はR3が支配的)が出力ノイズに大きく影響を与えていることがわかりました。ではR2 = 90Ω、R3 = 10Ωとして二桁抵抗の大きさを下げてみてみましょう。
NI Multisimでシミュレーションしてみる
図5はこの定数にした回路、そして図6はR2 = 90Ω、R3 = 10Ωとしたときのマーカ・リードアウトです。
図5、図6のR2 = 90Ω、R3 = 10Ωの条件ではonoise_spectrumと比較して、出力ノイズにR3が影響を与える量(onoise_rr3)が1/7(dBだと-8.7dB…電力相当なので20logではありません)でほとんど影響がなくなっていることが判ります。
抵抗値を小さくしてみるとAD797のスペックに近くなる
inoise_spectrumはV2の量ですから、この値のルートをとってみると、0.99nV/√Hzになります。この結果はAD797のスペックにだいぶ近づいていることがわかります。

図5. 抵抗値をR2 = 90Ω、R3 = 10Ωとした
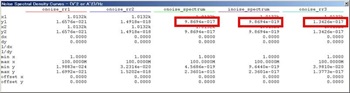
図 6. 抵抗値をR2 = 90Ω、R3 = 10Ωとしたときのマーカ・リードアウト
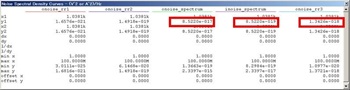
図7. 抵抗値をR2 = 9Ω、R3 = 1Ωとしたときのマーカ・リードアウト
さらに帰還抵抗を小さくしてみた
現実とすれば、これはこれで十分なのですが、再度R2 = 9Ω、R3 = 1Ωの条件で計算させてみました。
NI Multisimでシミュレーションしてみる
図7はこのR2 = 9Ω、R3 = 1Ωとしたときのマーカ・リードアウトです。inoise_spectrumの値のルートをとってみると、0.92nV/√Hzになっています。これはAD797のスペックどおりで、シミュレーション上でも良好な結果が出ていることがわかります。いずれにしてもR2 = 90Ω、R3 = 10Ωの条件と比較しても、0.6dBしか違いませんので、R2 = 90Ω、R3 = 10Ωでもほぼ十分な特性であることがわかります。
実回路では抵抗値は小さすぎなので適切なところを見つける
といっても、いずれにしてもR2 = 90Ω、R3 = 10Ωというのは、普通に考えても小さめな抵抗値です。出力振幅が大きい場合は電流制限でアウトになるところです。ここは小信号で増幅させ後段で再度増幅させること、もしくはR3を小さく、R2を大きくして利得を大きくすることが対策となるでしょう。
実際問題としては、OPアンプのノイズと比較して、周辺抵抗により生じるノイズ量[V/√Hz]が1/2程度になるくらいで(-6dB)十分でしょう。
10ΩのR3から発生するノイズ量は
ここで図5においてR3 = 10Ωのときのonoise_rr3を計算してみましょう。図5でR3から発生するノイズ量は、
SQRT(4 k T R) [V/√Hz]
で、R = 10ΩですからVNR3 = 4.07E-10 V/√Hzになります。これがR2とR3で分圧されて、その接続点の電圧VNCになりますから
VNC = VNR3×90/(10 + 90) = 3.66E-10 V/√Hz
と計算できます。これはonoise_rr3の入力換算 = (VNC)2ですから、2乗して1.342E-019と計算でき、それが利得AのA2 = 100倍され、
onoise_rr3 = 1.342E-017 V/√Hz
という図6でのマーカ読み値になるわけです。
R2の影響が少なくなるのはOPアンプの出力につながっているから
一応補足ですが、R2の影響が少なくなる理由を説明しておきます。OPアンプの出力抵抗は低く、出力は交流的にグラウンド接続とほぼ同じ(等価)になります。そのためR2の影響度は、R2とR3で分圧された量になり、影響度が低減することになります。
入力換算等価「電流源」にしてみる
それでは、一部繰り返しになりますが、入力換算等価電圧源を「電流源」としたときに、この等価「電流」源がノイズ源としてどれだけの大きさになるかを計算してみます。図8をご覧ください。電圧源が電流源に置き換わっています。
電圧ノイズ量を再確認
図7の抵抗値をR2 = 9Ω、R3 = 1Ωとしたときのonoise_spectrumは8.5225E-17 V2/Hzでした。それを1/102 = 1/100で入力換算した8.5225E-19 V2/Hz、そのルート、VN = 9.232E-10 V/√Hz(0.92nV/√Hz)が入力換算された電圧ノイズ量VNになります。

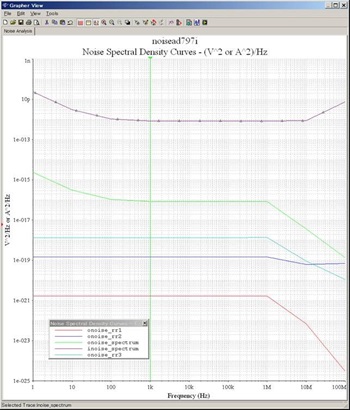
図9. 図8のシミュレーション結果
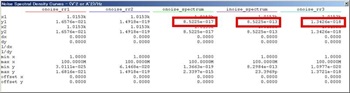
図10. 電流源にした図8のときのマーカ・リードアウト

電流源に再変換してみる
これを電流源として再換算してみると、このVNを生じさせるための電流量INは(OPアンプの非反転入力には電流は流れないので、全てR1に流れることになり)、R1 = 0.001Ω(1mΩ)なので
IN = V/R1 = 9.232E-10/0.0001 = 9.232E-7 A/√Hz
になります。図10はこのときのマーカ・リードアウトを示していますが、さきの電流量INを2乗した値、8.5225E-13 A2/Hzがinoise_spectrum(電流量)、入力換算電流源の大きさとして表されていることになっています。
信号源抵抗R1の大きさが非常に小さいため、電流量としては見かけ上大きくなっています。逆にいうと「信号源抵抗が小さければ、電流性ノイズの影響を受けにくい」といえます。
このため結局この回路は、OPアンプAD797の電圧性ノイズ(入力換算で0.9 nV/√Hz typical)が支配的なわけです。
信号源抵抗を大きくしてみる
信号源抵抗R1を1kΩにしたときにどうなるか考えてみます。今度はOPアンプの電流性ノイズ(入力換算で2 pA/√Hz typ)の影響がでてくるのです。入力換算等価電流源を「電圧源」に戻してシミュレーションしてみます。図11をご覧ください。
1kΩ相当のジョンソン・ノイズ量が得られている
信号源抵抗R1を1kΩにしたので、R1から出力に現れるノイズは
onoise_rr1 = 1.6575E-15 V2/Hz
に大きくなっています。これは出力ノイズ量なので、入力換算で1.6575E-17 V2/Hzとなり、このルートを取って電圧量VNR1にすると
VNR1 = 4.07nV/√Hz
で、1kΩから生じるジョンソン・ノイズの量そのままです。
ジョンソン・ノイズとAD797の入力換算電圧ノイズを足してみたら
これに合わせて、これまでの話のAD797の入力換算電圧ノイズ量
VNOP = 9.232E-10 V/√Hz(0.92nV/√Hz)
が電圧ノイズと存在しています。
そこで、それぞれのノイズ量を二乗し足し算して、出力換算として102倍してonoise_spectrumになるかを計算してみます。
(VNR1)2 = (4.0712E-9)2 = 1.6575E-17 V2/Hz×100
= 1.6575E-15 V2/Hz
(VNOP)2 = (9.232E-10)2 = 8.5229E-19 V2/Hz×100
= 8.5229E-17 V2/Hz
1.6575E-15 + 8.5229E-17 = 1.7427E-15 V2/Hz
になります。あれ…?図11では
onoise_spectrum = 2.3336E-15 V2/Hz
でここまでの計算より大きいですね!
AD797の電流性ノイズが原因だった
この大きい差異がどうなっているか再計算してみます。
onoise_spectrum - (出力に現れるR1ノイズ1.6575E-15)
- (出力に現れるOPアンプ電圧ノイズ8.5229E-17)
= 0.5909E-15 V2/Hz
が差異のノイズ量です。入力換算ですと、1/100で、0.5909E-17 V2/Hzです。これをルートを取ってノイズ電圧量にします。2.4308E-9 V/√Hzになっています。R1 = 1kΩでノイズ電圧量を割ると、電流量としては
2.4308E-12 A/√Hz = 2.4pA/√Hz
です!これは最初に示した「INPUT CURRENT NOISE」の大きさとほぼ同じです。つまりこの差異はAD797の電流性雑音が影響を与えた分になっているのです。この電流性雑音がR1に流れ、R1で電圧降下が発生し、ノイズ電圧になって出力に出てきているんですね!
ここまでのポイント
ここまでの流れからそのポイントとして、
- AD797が電圧性ノイズが低く、電流性ノイズが高めである
- そのためある信号源抵抗を境にして、電流性ノイズの方が支配的になっていく
ということになります。これらにより信号源抵抗の高い場合には、電流性ノイズが低いOPアンプの必要性も理解いただけるものと思います。
全体のrmsノイズ量を求めてみる
あらためて、さきの(図11の)
onoise_spectrum = 2.3336E-15 V2/Hz
という「1Hz密度」がどの程度の量なのか、考えてみましょう。
たとえば-3dB帯域が1MHzのシステムで考えますと、これが1次系(-6dB/Octで低下する)のフィルタとしてみた場合、全体のノイズ量は
onoise_spectrum×1E6×1.57 = 3.664E-9 V2
になります。1.57という係数は、一次フィルタの-3dB周波数をf [Hz]として、そのフィルタを通したときの全rmsノイズ量が、帯域幅BW [Hz]の矩形フィルタを通したときの量と同じとしたとき
BW = 1.57 × f
と計算されるためです。つまり帯域補正係数です。上記の数値のルートを取ると、60μV (rms)になります。
rms値からピーク値にするには6倍~6.6倍
話しが少しややこしいので、細かい話は飛ばしますが、このピーク値は6倍とか6.6倍と「概算」され、6倍だと360μV = 0.36mV (peak)になります。結構大きくなるものですね。
ノイズはガウス分布をしているので、6倍とか6.6倍というのは、この大きさを超えるノイズピークの発生確率が誤差の範囲(ほぼゼロ)として考えてよいという概算値です。品質管理のσの計算と実は同じなんです。
システムによっては帯域幅BWを出来るだけ狭くして、SN比を向上させる、というやりかたも取ります。
「等価ノイズ抵抗」という概念がある
数字ばっかりが並んでつまらなくなってきたかもしれません(汗)。そろそろ終わりにしましょう(笑)。信号源抵抗R1が1kΩのときには、
- R1から生じるノイズ量
VNR1 = 4.07 nV/√Hz - OPアンプAD797の入力換算電圧ノイズ
VNV = 0.923 nV/√Hz - OPアンプAD797の電流性ノイズ(2.4pA/√Hz)が信号源抵抗R1に流れて生じる電圧
VNI = 2.43 nV/√Hz
というふうにまとめられます。ここで
VNI > VNV
になっていますね。信号源抵抗R1が大きくなると、あるところで電流性ノイズの影響が電圧性ノイズを越してしまいます。その(ところの)信号源抵抗の大きさRNは、
RN = 電圧性ノイズ/電流性ノイズ(それぞれ入力換算)
= 0.923 [nV/√Hz]/2.43 [pA/√Hz] = 380Ω
と計算できます。この計算により得られた値を「等価ノイズ抵抗RN」と言います。ただしここでは電流ノイズは入力の片側の端子だけで考えていますので、もう一方の端子にも抵抗がつながっている場合は、それも考慮する必要があります。
いずれにしても、ここまでの説明をベースにシミュレーションしてみれば、一発で答えが出ますから、NI Multisimで是非遊んでみてください。
現実の信号源には信号源抵抗がある
さて、ここまで「信号源抵抗がある」ことと、「信号源抵抗が大きいときは別のOPアンプを」という話、そしてノイズを生じる要素として、
- 信号源抵抗
- OPアンプの電圧性ノイズ(入力換算)
- OPアンプの電流性ノイズ(入力換算)
というお話をしてきました。しかし「信号源抵抗をなぜここまで気にするの?」という疑問が出てくると思います。
普通、信号源は電圧源で考えることが多いわけで、「電圧源=内部抵抗ゼロ」と思いがちだと思います。
しかし実際のいろいろな自然界の信号、たとえばマイクの音声入力、センサ入力などなど、低いものでも数Ωから数10Ω、多い種類のところで数kΩ、高いもので数GΩなど、信号源となるモノには出力抵抗成分が存在します。
フォト・ダイオードは信号源抵抗が高い
たとえばフォト・ダイオードなどは、電流電圧変換回路(トランス・インピーダンス)になるわけで、定電流出力のフォト・ダイオードはOPアンプの反転入力(バーチャル・ショート)のところに接続されます。
しかし、定電流というのは信号源インピーダンス(抵抗)が高いことと同じであり、ここまでの話しで、OPアンプ入力に高い信号源抵抗がつながっていることと等価です。つまり電流性ノイズが支配的になりますから、電流性ノイズの低いOPアンプを選定する必要があるわけですね。
信号源抵抗から生じるノイズに影響に与えない回路を実現することがこの技術ノートの趣旨
信号源抵抗からのノイズを無くすのは無理にしても(技もありますが)、「OPアンプで、ノイズを最適に少なくして、増幅する必要がある」というのがこの技術ノートの趣旨だったのです。
また入力抵抗のノイズ自体もどのくらいあるかを、SN比という視点で十分に考慮が必要だということなんですね。
まとめ
ここまでOPアンプのノイズには、電圧性と電流性があり、信号源抵抗の大きさとOPアンプの種類で、どちらが支配的になるかが決まる、とお話してきました。
繰り返しになりますが、結局はここまでの理解をベースにNI Multisimでシミュレーションしてみれば、難しい計算に悩むことなく答えが出る!というわけです。
参考文献
アナログ・デバイセズのウェブ・サイトのRAQ(Rarely Asked Questions; 珍問/難問集)に、OPアンプと抵抗のノイズに関係する話題がアップされていますので、最後にご紹介しておきます。アナログ・デバイセズのエンジニア、James Bryantによる記事です。技術的なノウハウが得られる息抜きの記事です。是非ご覧ください。
- 私の低ノイズ・アンプはあまり低ノイズではありません。どこか間違えているのでしょうか?
- 前回、オペアンプのノイズを外部抵抗のせいにされました。いつもそうとは限らないと思うのですが、いかがでしょうか?
- Operational Amplifier Noise(上記のまじめな関連記事:英語)
- 抵抗(と老婦人)には秘められた深みがある
- Resistors in Analog Circuitry(上記のまじめな関連記事:英語)

著者について
デジタル回路(FPGAやASIC)からアナログ、高周波回路まで多...




















