目的
今回の実習では、PN接合ダイオードの電流/電圧(I-V)特性を計測します。
実習項目
- 2a:半波整流器
- 2b:全波整流器
- 2c:ブリッジ整流器
- 2d:リミッタ/クランプ回路
- 2e:AC結合とDC復元
- 2f:可変アッテネータ
- 2g:絶対値回路
- 2h:電圧ダブラ回路
準備するもの
- アクティブ・ラーニング・モジュール「ADALM2000」
- ソルダーレス・ブレッドボード
- 抵抗:1kΩまたは1kΩ~5kΩの任意の値のもの(1個)
- 小信号ダイオード:「1N914」またはそれに準ずるもの(1個)
説明
PN接合ダイオードのI-V特性は、ADALM2000を使用し、図1のように接続することで測定できます。図中の青色の四角形は、ADALM2000のどこに接続するのかを表しています。ブレッドボードのセットアップとしては、まず抵抗の一端に任意波形ジェネレータ(AWG)の出力W1を接続します(図2)。オシロスコープの入力2+もここに接続します。抵抗のもう一端は図のとおりダイオードの一端に接続します。この抵抗端には、オシロスコープの入力2-と1+も接続します。ダイオードのもう一端は、オシロスコープの入力1-とグラウンドに接続します。

ハードウェアの設定
AWGは、振幅が6V、オフセットが0V、周波数が100Hzの三角波を生成するように設定します。オシロスコープのチャンネル2(差動入力の2+と2-)により、抵抗(とダイオード)の電流を測定します。オシロスコープのチャンネル1(シングルエンド入力の1+)は、ダイオードの電圧の測定に使用します(1-はグラウンドに接続します)。オシロスコープのチャンネル1とチャンネル2は、どちらも500mV/divに設定します。ダイオードに流れる電流IDは、チャンネル2で測定した電圧を抵抗値(この例では1kΩ)で割った値になります。XY表示モードを使用し、ダイオードの電圧(オシロスコープのチャンネル1)をX軸、ダイオードの電流(オシロスコープのチャンネル2)をY軸とするグラフを表示します(図3)。.

手順


取得したデータを「Excel」などの表計算ソフトに読み込み、ダイオードの電流IDを計算します。そして、ダイオードの電流と電圧の関係を表すグラフを作成します(図4)。ダイオードの電圧と電流は対数の関係になります。対数スケールで表示すると、図5に示すように、グラフはほぼ直線になるはずです。
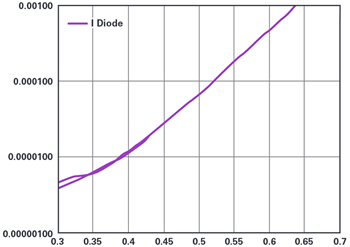
問題
ダイオードの電圧VDとダイオードの電流IDの関係を表す式は、どのようになりますか。
ダイオードの特性に関する追加の演習
1N914を複数個用意し、それぞれの特性(一定のIDに対するVD)を計測してみましょう。1N914は、アナログ・パーツ・キット「ADALP2000」に4個付属しています。他の人と交換すれば、より多くのサンプルを対象として測定を実施できます。測定が終わったら、取得した値の平均値と変動係数(CV:Coefficient of Variation)を計算してください(CVは、標準偏差を平均値で割った値をパーセント単位で表したものです)。どのような結果が得られるでしょうか。このばらつきが、半導体技術者がプロセスばらつきと呼ぶ指標です。
続いて、1N914をLED(発光ダイオード)に置き換えてみましょう。ADALP2000には、それぞれ赤色、黄色、緑色、赤外線に対応するLEDが含まれているはずです。LEDでも、VDからIDを計算する式は、1N914と同じになるのでしょうか。類似点と相違点を挙げてください。また、赤色、黄色、緑色の各LEDは、同じ順方向電圧で点灯するでしょうか。
2a:半波整流器
目的
この実習では、ダイオードを半波整流器として使用し、その動作を確認します。
準備するもの
- 抵抗:4.7kΩまたはそれに準ずるもの(1個)
- 小信号ダイオード:1N914またはそれに準ずるもの(1個)
説明
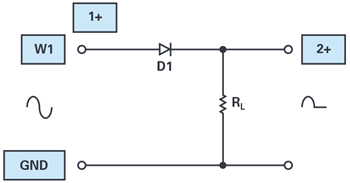
ブレッドボードのセットアップとしては、まず、AWGの出力W1をダイオードの一端に接続します(図6、図7)。ダイオードのもう一端は、負荷抵抗の一端に接続します。抵抗のもう一端は、グラウンドに接続します。オシロスコープのチャンネル2(シングルエンド入力の2+)は、抵抗とダイオードを接続したノードに接続します(2-はグラウンドに接続することができます)。
ハードウェアの設定
AWGは、振幅が6V、オフセットが0V、周波数が100Hzの正弦波を生成するように設定します。オシロスコープのチャンネル2(2+)により、負荷抵抗RLの電圧を測定します。オシロスコープのチャンネルは、いずれも500mV/divに設定します。.

手順
アナログ・デバイセズのソフトウェア・パッケージ「Scopy」のオシロスコープ機能を使用して、2つの波形をグラフに表示します。

問題
半波整流器の出力のピーク値がAC入力のピーク値よりも小さくなるのはなぜでしょう。また、どれだけ小さくなりますか。入力波形が(ゼロではなく)どのようになったときに、整流器の出力波形は正の値になるのでしょうか。更に、ダイオードの向きを逆にするとどうなりますか。ダイオードの向きを逆にして、同じ実験を繰り返してみてください。
追加の演習
1N914をLEDに置き換えてみましょう。なお、LEDの方が順方向の降下電圧が大きいので、おそらくAWGのチャンネル1では、振幅を10Vに設定する必要があります。
- 1N914を使用した場合と比べて、整流器の出力波形はどのように変化しますか。また、順方向の電圧降下はどれだけ増加しますか。
- AWGにおいて、周波数を100Hzに設定したままで波形だけ変更してみます。3つの異なる波形に対し、LEDの輝度はどのように変化しますか。波形と輝度についてはどのような結果が観測されましたか。その結果と各波形のDCの測定値(実効値)には、どのような関係がありますか
- AWGにおいて、出力周波数を0.2Hz(5秒で1サイクル)まで下げて実験を行います。周波数が1Hz以下の場合、3つの各波形に対するLEDの光強度はどのようになりますか。
- LEDの点灯にちらつきがなくなり、強度が一定になるのは、周波数がいくつのときですか。
2b:全波整流器
目的
この実習では、ダイオードを使用して全波整流器を構成し、その動作を確認します。
準備するもの
- 抵抗:4.7kΩまたはそれに準ずるもの(1個)
- 小信号ダイオード:1N914またはそれに準ずるもの(2個)
説明
ブレッドボードのセットアップとしては、まず、W1を1つ目のダイオードD1の一端に接続します(図9、図10)。また、W2を2つ目のダイオードD2の一端に接続します。2つのダイオードは同じ向きに接続します。各ダイオードのもう一端は、負荷抵抗の一端に接続します。抵抗のもう一端は、グラウンドに接続します。オシロスコープのチャンネル2(シングルエンド入力の2+)は、抵抗と2つのダイオードを接続したノードに接続します。
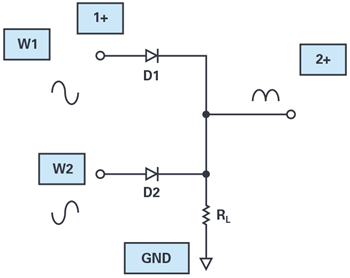
ハードウェアの設定
AWGのW1は、振幅が6V、オフセットが0V、周波数が100Hzの正弦波を生成するように設定します。AWGのW2も同じ設定にしますが、位相だけ180°変えておきます。オシロスコープのチャンネル2(シングルエンド入力の2+)によって、負荷抵抗の電圧を測定します。オシロスコープのチャンネルは、いずれも500mV/divに設定します。
手順
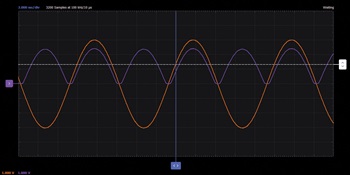
Scopyのオシロスコープ機能を使用して、2つの波形をグラフとして表示します。位相がそれぞれ0°と180°のAC入力を使用した場合、2つ目のダイオードによって入力の欠けている半波が補われ、図11に示すような全波整流信号が生成されます。ダイオードには順方向電圧が存在し、ターンオンする電圧はゼロではないので、ゼロと交差する部分の出力波形はシャープにはなりません。
問題
ダイオードの向きを逆にするとどうなりますか。両方のダイオードの向きを逆にして、同じ実験を繰り返してみてください。
片方のダイオードだけ向きを逆にするとどうなりますか。ダイオードD1の向きを逆にして、同じ実験を繰り返してみてください。
1つのソース(トランスなど)を基に0°と180°という位相の異なる信号を生成するには、どうすればよいですか。
追加の演習
D1とD2を赤色LEDと緑色LEDに置き換えてみましょう。なお、LEDの方がターンオンする電圧が高いので、AWGのチャンネル1では振幅を10Vに設定します。また、AWGのチャンネル1の周波数は5Hz以下に設定します。2つのLEDが同時に点灯することはありますか。
- 1N914を使用する場合と比べて、整流器の出力波形はどのように変化しますか。順方向の電圧降下はどれだけ増加しますか。
- AWGにおいて、周波数は100Hzに設定したままで波形だけ変更してみます。3つの異なる波形に対し、LEDの輝度はどのように変化しますか。波形と輝度については、どのような結果が観測されましたか。その結果と各波形のDCの測定値(実効値)には、どのような関係がありますか。
- AWGにおいて、出力周波数を0.2Hz(5秒で1サイクル)まで下げて実験を行います。周波数が1Hz以下の場合、3つの各波形に対するLEDの光強度はどのようになりますか。
- LEDの点灯にちらつきがなくなり、強度が一定になるのは、周波数がいくつのときですか。
2c:ブリッジ整流器
目的
この実習では、4つのダイオードを使用してブリッジ整流器を構成し、その動作を確認します。
準備するもの
- 抵抗:4.7kΩまたはそれに準ずるもの(1個)
- 小信号ダイオード:1N914またはそれに準ずるもの(4個)
説明
図12と図13に示すように、4つのダイオードを使ってブリッジ回路を構成にすることで、1つのAC信号に対して全波整流を施すことができます。この図からわかるように、グラウンドを基準にできるのはAC入力または負荷だけです。

ハードウェアの設定
AWGは、振幅が6V、オフセットが0V、周波数が100Hzの正弦波を生成するように設定します。オシロスコープのチャンネル2(2+と2-)によって、負荷抵抗RLの電圧を測定します。オシロスコープのチャンネルは、いずれも500mV/divに設定します。

手順
Scopyのオシロスコープ機能を使用して、2つの波形をグラフに表示します。この回路の欠点は、2つのダイオードの降下電圧が負荷と直列に生じることです。それにより、整流器の出力のピーク値とAC入力との差が、先ほどの回路では0.6Vだったのに対し、この回路では1.2Vまで広がることです。

問題
図8では、ACソースの一端をグラウンドに接続していました。図12の回路の場合、どのように変更すれば、負荷抵抗の一端をグラウンドに接続できるようになりますか。
追加の演習
4つのダイオードD1、D2、D3、D4を赤色LEDと緑色LEDに置き換えてみましょう。LEDの方がターンオン電圧が高いので、AWGのチャンネル1では振幅を10Vに設定します。また、AWGのチャンネル1の周波数は5Hz以下に下げます。2つのLEDが同時に点灯することはありますか。その場合、同時に点灯するのはどの2つですか。
- 1N914を使用する場合と比べて、整流器の出力波形はどのように変化しますか。順方向の電圧降下はどれだけ増加しますか。
- AWGにおいて、周波数を100Hzに設定したままで波形だけ変更してみます。3つの異なる波形に対し、LEDの輝度はどのように変化しますか。波形と輝度については、どのような結果が観測されましたか。その結果と各波形のDCの測定値(実効値)には、どのような関係がありますか。
- AWGにおいて、出力周波数を0.2Hz(5秒で1サイクル)まで下げて実験を行います。周波数が1Hz以下の場合、3つの各波形に対するLEDの光強度はどのようになりますか。
- LEDの点灯にちらつきがなくなり、強度が一定になるのは、周波数がいくつのときですか。
2d:リミッタ/クランプ回路
目的
この実習では、ダイオードを使用して振幅を制限するクランプ回路(クランプ回路)を構成し、その動作を確認します。
準備するもの
- 抵抗1個:10kΩまたはそれに準ずるもの(1個)
- 小信号ダイオード:1N914またはそれに準ずるもの(2個)
説明
図15と図16に示すように、まずはAWGの出力W1を10kΩの抵抗の一端に接続します。1つ目のダイオードD1は、10kΩの抵抗のもう一端とAWGの出力W2の間に接続します。2つ目のダイオードD2は、図のように、D1のもう一端とグラウンドの間に接続します。オシロスコープのチャンネル2(2+)は、抵抗と2つのダイオードを接続したノードに接続します。

ハードウェアの設定
AWGのチャンネル1は、振幅が6V、オフセットが0V、周波数が100Hzの正弦波を生成するように設定します。AWGのチャンネル2は初期値として振幅が0V、オフセットが0Vと設定しますが、その後、オフセットの値を変化させて出力信号への影響を観測します。オシロスコープのチャンネル2(2+)によって、クランプ(制限)された電圧を観測します。オシロスコープのチャンネルは、いずれも500mV/divに設定します。

手順
AWGのチャンネル2においてDCオフセットの値をゼロにし、オシロスコープのチャンネル2(2+)で電圧の最小値と最大値を観測します。続いて、AWGのチャンネル2においてDCオフセットの値を-2V~2Vの範囲で変化させ、電圧の最小値と最大値を求めます。また、D1とD2の向きを逆にし、DCオフセットの値を変化させて電圧の最小値と最大値を求める作業を繰り返します。2つの測定結果にはどのような違いがあるでしょうか。

問題
D1とD2をAWGのチャンネル2に接続すると、電圧の制限動作にはどのような変化が生じますか。
2e:AC結合とDC復元
目的
この実習では、AC結合と、ダイオードをDC復元回路として使用する場合の動作を確認します。多くの信号にはDC成分が含まれます。このDC成分を除去しなければならないケースは少なくありません。また、そうした場合も、信号パスの後段で異なるDCレベルを復元しなければならなくなることがよくあります。
準備するもの
- コンデンサ:1.0μFまたはそれに準ずるもの(1個)
- 小信号ダイオード:1N914またはそれに準ずるもの(1個)
説明
図18と図19に示すように、まずはW1を1.0μFのコンデンサの一端に接続します。ダイオードD1は、1.0μFのコンデンサのもう一端とAWGのW2の間に接続します。オシロスコープのチャンネル2(シングルエンド入力の2+)は、コンデンサとダイオードを接続したノードに接続します。

ハードウェアの設定
AWGのチャンネル1は、最初は振幅が2V、オフセットが0V、周波数が1kHzの正弦波を生成するように設定しますが、その後オフセットの値を変化させて、出力への影響を観測します。AWGのチャンネル2も最初は振幅を0V、オフセットを0Vとしておきますが、その後オフセットの値を変化させて出力への影響を観測します。オシロスコープのチャンネル2(2+)によって、電圧を測定します。オシロスコープのチャンネルはいずれも500mV/divに設定します。

手順
Scopyのオシロスコープ機能を使用して、2つの波形をグラフに表示します。

続いて、ダイオードD1を10kΩの抵抗に置き換えます。オシロスコープの測定タブを使用し、AWGのチャンネル1のオフセットを-1~1Vの間で変化させながら、チャンネル2(2+)において、正と負のピーク値と平均値を読み取り記録します。次に、AWGのチャンネル1において、振幅は2Vのままで波形を方形波に変更します。先ほどと同様に、方形波のデューティ・サイクルを10%~90%の間で変化させながら、正と負のピーク値と平均値を読み取り記録します。続いて、10kΩの抵抗をダイオードD1に戻します。DCオフセットとデューティ・サイクルの値を変更して、抵抗の場合と同じ測定を繰り返します。そうすると、どのような違いが観測されるでしょうか。更に、ダイオードD1の向きを逆にし、再び同じ測定を行います。前の2つの測定と比べて結果はどのように変化しますか。
問題
D1の向きを逆にするとどうなりましたか。AWGの出力W2として異なるDC値を設定すると、どのような影響が生じますか。
2f:可変アッテネータ
目的
この実習では、ダイオードを使って小信号に対応する可変アッテネータを構成し、その特性評価と解析を行います。
準備するもの
- 抵抗:2.2kΩ(1個)、4.7kΩ(1個)、10kΩ(1個)、
- 可変抵抗(ポテンショメータ):5kΩ(1個)
- コンデンサ:0.1μF(2個)
- 小信号ダイオード:1N914またはそれに準ずるもの(1個)
説明
図21と図22に示すように、AWGのW1を0.1μFのコンデンサC1の一端に接続します。抵抗R1は、C1のもう一端とD1/R2/C2を接続したノードの間に配置します。D1のもう一端はグラウンドに接続します。抵抗R2のもう一端は、ポテンショメータR3のワイパーに接続します。R3はグラウンドとVp(5V)の間に配置します。オシロスコープのチャンネル2(2+)は、コンデンサC2と負荷抵抗R4を接続したノードに接続します。

ハードウェアの設定
AWGのW1は、振幅が200mV(またはそれ以下)、オフセットが0V、周波数が10kHzの正弦波を生成するように設定します。オシロスコープのチャンネル1(1+)は100mV/divに設定し、同チャンネル2(2+)は100mV/divに設定してR4に接続します。チャンネル1のピークtoピークとチャンネル2のピークtoピークが表示されるように測定タブを設定します。

手順
Scopyのオシロスコープ機能を使用して、2つの波形をグラフに表示します。

C1(とC2)を使用する目的は、入出力回路からのDC成分を遮断し、ダイオードの動作点に影響が生じないようにすることです。このアッテネータ回路では、ダイオードの小信号抵抗rDがダイオードに流れるDC成分IDの関数であることを利用します(以下参照)。

各変数の意味は以下のとおりです。
n:ダイオードの面積のスケール・ファクタ
VT:熱電圧
ID:ダイオードの電流
k:ボルツマン定数
q:電荷量
T:絶対温度
この回路では、R1とD1の抵抗値によって分圧器が構成されます。R2の電流を変えることによって、D1の電流を変化させます。D1の電流が少ない場合、rDは大きく、出力に表れる入力信号成分は大きくなります。D1の電流が多くなるにつれてその抵抗値は低下し、出力に表れる入力信号成分は減衰します。
問題
出力信号を歪ませることなく使用できる最大入力信号レベルを調べてください。回路におけるどのパラメータが入力信号の上限値を左右しますか。
2g:絶対値回路s
目的
この実習では、絶対値回路の動作を確認します。絶対値回路(整流器)は、AC信号の振幅を、より容易に測定できるDC値に変換するための検波器としてよく使用されます。この種の回路では、まずハイパス・フィルタによってAC信号のDC成分を除去します。次に、得られた信号を整流し、おそらくはローパス・フィルタを適用することになります。ダイオードで構成したシンプルな整流器で観測したように、この回路は、ダイオードの降下電圧(シリコン・ダイオードで0.6V)より振幅が小さい信号にはうまく反応しません。つまり、小振幅の信号の測定には使用できないことがあります。高い精度が求められる場合には、ダイオードと共にオペアンプを使用することで、高精度の整流器を構成することができます。
準備するもの
- デュアルオペアンプ:「ADTL082」またはそれに準ずるもの(1個)
- 抵抗:10kΩ(5個)
- 小信号ダイオード:1N914またはそれに準ずるもの(2個)
- コンデンサ:4.7μF(2個、デカップリング用)
説明
図24と図25に示すように、反転増幅回路に2つのダイオードを追加することで、理想的な(リニア精度の)半波整流器を構成することができます。入力が負である場合、ダイオードD1に逆バイアス、D2には順バイアスがかかり、回路はゲインが-1の典型的なインバータとして動作します。一方、入力が正である場合には、ダイオードD1に順バイアスがかかり、アンプ回路に帰還パスが形成されます。ダイオードD2には逆バイアスがかかり、出力がオペアンプから切り離されます。出力の電圧は、10kΩの抵抗を介して実質的にグラウンド(アンプの反転入力端子)のレベルになります。


手順
図26に示すように、この半波整流器では、出力のピーク値が入力のピーク値と等しくなります。入力がゼロを交差する際の遷移も急峻です。回路の複数のポイントで波形を観察し、この回路がダイオードをベースとするシンプルな半波整流器よりも優れている理由を考察してみてください。

説明
図27に示した回路が絶対値回路です。これも高精度の全波整流器だと表現することもできます。理想的なダイオード(順方向に電圧を印加した場合の電圧が0V)で構成した全波整流器のように動作します。回路に使われている実際のダイオードの順方向電圧は約0.6Vです。


図28. ブレッドボードにおける絶対値回路の接続図

手順
以下の手順で実習を進めてください。
- 回路の電圧/電流を調べて、その動作を把握してください。この回路の動作を理解する上では、非常に基本的な概念を知っておく必要があります。オペアンプを使って負帰還回路を構成すると、反転入力端子と非反転入力端子の電圧は、同じレベルに近づきます。これを仮想短絡と呼びます。
- この回路が絶対値回路として機能することを確認するために、複数のテストのプランを考えてください。また、それらのテストを実施し、すべての結果を文書として記録してください。
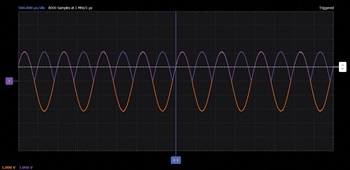
- 入力電圧を振幅が6Vで周波数が1kHzの正弦波とします。回路のすべてのノードの電圧を慎重に測定して記録してください。
問題
すべてのテストの内容と結果を文書として記録し、レポートを作成してください。
2h:電圧ダブラ回路
電圧ダブラは、システムの電源電圧よりも高いDC電圧が必要で、負荷電流が比較的少ない場合に非常に便利な回路です。

この回路の動作は、ここまでに取り上げたダイオード・ベースの整流器ほど単純明快なものではありません。この回路について理解するには、AWGのW1で生成するAC入力の1/2サイクルの動作を詳細に観察する必要があります。まず、ここでは理想的な部品が使われていて、C1 = C2であると仮定します。
- 最初の負の1/2サイクルでは、D1に順バイアスがかかり、C1の右端の電圧がグラウンドよりもダイオード1個の降下電圧分だけ低い値になるように維持されます。C1は、AC入力のピーク電圧VPEAKにほぼ等しい電圧に充電され、左端の電圧はグラウンドに対して負になります。
- 続く正の1/2サイクルにおいて、D1には逆バイアスがかかり、電流が流れなくなります。C1の電圧がAC入力電圧に加算され、D2の左端の電圧はVPEAKの約2倍になります。C2はまだ全く充電されておらず、D2には順バイアスがかかって、C1の右端の電圧がC2の上部に印加されます。C1の放電に伴ってC2が充電され、両コンデンサはD2に順バイアスをかけられない状態に達します。最初の正の1/2サイクルでは、C2の電圧はVPEAKに等しくなります。C1は完全に放電するので、D2の左端の電圧はすべてAC入力によるものとなります。
- 次の負の1/2サイクルにおいて、C1はD1によって再びVPEAKまで充電されます。C2を放電するための負荷がない場合、その出力はVPEAKのままになります。
- 次の正の1/2サイクルでは、C2はVPEAKに充電されたままですが、D2の左端の電圧は再びVPEAKの約2倍になります。先ほどと同様に、C1の電荷の一部がC2に移りますが、今度はC2がVPEAKの1.5倍に達した時点で停止します。
- 上記の動作がサイクルごとに繰り返されます。C1は、負の1/2サイクルごとにVPEAKまで完全に充電され、C2を充電します。C2は、開始時の電圧と2×VPEAKの中央値まで充電されます。C2は2×VPEAKに達することはありませんが、その値に近づいていきます。
現実の部品は、理想的な部品とは異なります。すなわち、各ダイオードに順バイアスをかけると、電圧降下(この場合、0.6V)が生じます。それにより、電圧ダブラ回路における無負荷時の最大出力電圧が低下します。RLなど、この回路の任意の負荷によって必ずC2から電流が引き出されるので、C2の電荷はある程度放電されます。正の1/2サイクルごとに、C1は、1/2サイクルの開始時の電圧と2×VPEAKの中央値までC2を再充電します。出力リップルは大きく、平均DC値は小さくなっていきます。
この回路の出力電流容量は、通常の整流器の半分しかないことに注意してください。電圧ダブラ回路から更に多くの負荷電流が引き出されると、C2は更に早く放電するようになり、出力電圧は低下します。入力される以上の電力を電圧ダブラ回路から引き出すことはできません。
C1をC2よりも大きくすると、C2の充電と再充電を高速化することができます。C1を10μF、C2を1μFとすると、C1は正の1/2サイクルごとにはるかに多くの電荷をC2に移すことができます。そのため、C2の電圧は、C1の電圧が低下するよりもはるかに早いペースで上昇します。当然のことながら、これは、出力電流容量が更に制限されるということも意味します。C2の充電が高速化されると同時に、放電も高速になるということです。

手順
Scopyのオシロスコープ機能を使用して、2つの波形をグラフに表示します。

問題
図30に示した回路は、正のDC出力電圧を生成します。負の出力電圧を生成するには、どのようにすればよいでしょうか。電圧インバータを構成し、実験/シミュレーションを繰り返してみましょう。
答えはStudentZoneで確認できます。


