Abstract
Three different methods to measure noise figure are presented: Gain method, Y-factor method, and the Noise Figure Meter method. The three approaches are compared in a table.
Introduction
In wireless communication systems, the "noise figure (NF)" or the related "noise factor (F)" is a number used to specify the performance of a radio receiver. The lower the value of noise figure, the better the performance. This tutorial discusses this important parameter in more detail and describes three different noise figure measurement procedures.
Noise Figure and Noise Factor
Noise Figure (NF) is sometimes referred to as Noise Factor (F). The relationship is simply:
NF = 10 * log10 (F)
Definition
Noise Figure (Noise Factor) contains the important information about the noise performance of a RF system. The basic definition is:
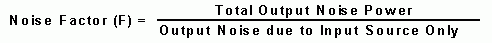
From this definition, many other popular equations of the Noise Figure (Noise Factor) can be derived.
| Category | MAXIM Products | Noise Figure* | Applications | Operating Frequency | System Gain |
| LNA | MAX2640 | 0.9dB | Cellular, ISM | 400MHz ~ 1500MHz | 15.1dB |
| LNA | MAX2645 | HG: 2.3dB | WLL | 3.4GHz ~ 3.8GHz | HG: 14.4dB |
| LG: 15.5dB | WLL | 3.4GHz ~ 3.8GHz | LG: -9.7dB | ||
| Mixer | MAX2684 | 13.6dB | LMDS, WLL | 3.4GHz ~ 3.8GHz | 1dB |
| Mixer | MAX9982 | 12dB | Cellular, GSM | 825MHz ~ 915MHz | 2.0dB |
| Receiver System | MAX2700 | 3.5dB ~ 19dB | PCS, WLL | 1.8GHz ~ 2.5GHz | < 80dB |
| * HG = High Gain Mode, LG = Low Gain Mode | |||||
Measurement methods vary for different applications. As shown in the table above, some applications have high gain and low noise figure (Low Noise Amplifiers under HG mode), some have low gain and high noise figure (mixers and LNAs under LG mode), some have very high gain and wide range of noise figure (receiver systems). Measurement methods have to be chosen carefully. In this article, a Noise Figure Meter as well as two other popular methods - "gain method" and "Y factor method" - will be discussed.
Using a Noise Figure Meter
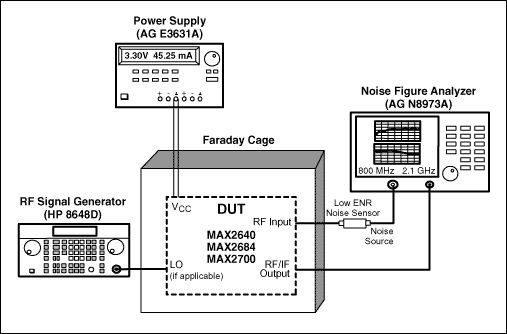
Noise Figure Meter/Analyzer is employed as shown in Figure 1.
The noise figure meter, such as Agilent N8973A Noise Figure Analyzer, generates a 28VDC pulse signal to drive a noise source (HP346A/B), which generates noise to drive the device under test (DUT). The output of the DUT is then measured by the noise figure analyzer. Since the input noise and Signal-to-Noise ratio of the noise source is known to the analyzer, the noise figure of the DUT can be calculated internally and displayed. For certain applications (mixers and receivers), a LO signal might be needed, as shown in Figure 1. Also, certain parameters need to be set up in the Noise Figure Meter before the measurement, such as frequency range, application (Amplifier/Mixer), etc.
Using a noise figure meter is the most straightforward way to measure noise figure. In most cases it is also the most accurate. An engineer can measure the noise figure over a certain frequency range, and the analyzer can display the system gain together with the noise figure to help the measurement. A noise figure meter also has limitations. The analyzers have certain frequency limits. For example, the Agilent N8973A works from 10MHz to 3GHz. Also, when measuring high noise figures, e.g., noise figure exceeding 10dB, the result can be very inaccurate. This method requires very expensive equipment.
Gain Method
As mentioned above, there are other methods to measure noise figure besides directly using a noise figure meter. These methods involve more measurements as well as calculations, but under certain conditions, they turn out to be more convenient and more accurate. One popular method is called "Gain Method", which is based on the noise factor definition given earlier:
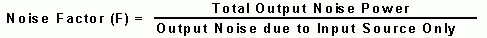
In this definition, "Noise" is due to two effects. One is the interference that comes to the input of a RF system in the form of signals that differ from the desired one. The second is due to the random fluctuation of carriers in the RF system (LNA, mixer, receiver, etc). The second effect is a result of Brownian motion, It applies in thermal equilibrium to any electronic device, and the available noise power from the device is:
PNA = kTΔF,
Where k = Boltzmann's Constant (1.38 * 10-23 Joules/ΔK),
T = Temperature in Kelvin,
ΔF = Noise Bandwidth (Hz).
At room temperature (290ΔK), the noise power density PNAD = -174dBm/Hz.
Thus we have the following equation:
NF = PNOUT - (-174dBm/Hz + 10 * log10(BW) + Gain)
In the equation, PNOUT is the measured total output noise power. -174dBm/Hz is the noise density of 290°K ambient noise. BW is the bandwidth of the frequency range of interest. Gain is the system gain. NF is the noise figure of the DUT. Everything in the equation is in log scale. To make the formula simpler, we can directly measure the output noise power density (in dBm/Hz), and the equation becomes:
NF = PNOUTD + 174dBm/Hz - Gain
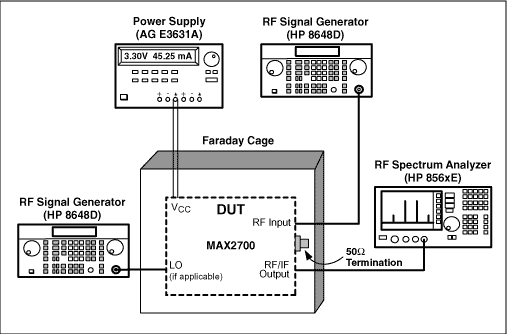
To use the "Gain Method" to measure the noise figure, the gain of the DUT needs to be pre-determined. Then the input of the DUT is terminated with the characteristic impedance (50Ω for most RF applications, 75Ω for video/cable applications). Then the output noise power density is measured with a spectrum analyzer.
The setup for Gain Method is shown in Figure 2.
As an example, we measure the noise figure of the MAX2700. At a specified LNA gain setting and VAGC, the gain is measured to be 80dB. Then, set up the device as show above, and terminate the RF input with a 50Ω termination. We read the output noise density to be -90dBm/Hz. To get a stable and accurate reading of the noise density, the optimum ratio of RBW (resolution bandwidth) and VBW (video bandwidth) is RBW/VBW = 0.3. Thus we can calculate the NF to be:
-90dBm/Hz + 174dBm/Hz - 80dB = 4.0dB.
The "Gain Method" can cover any frequency range, as long as the spectrum analyzer permits. The biggest limitation comes from the noise floor of the spectrum analyzer. As shown in the equations, when Noise Figure is low (sub 10dB), (POUTD - Gain) is close to -170dBm/Hz. Normal LNA gain is about 20dB. In that case, we need to measure a noise power density of -150dBm/Hz, which is lower than the noise floor of most spectrum analyzers. In our example, the system gain is very high, thus most spectrum analyzers can accurately measure the noise figure. Similarly, if the Noise Figure of the DUT is very high (e.g., over 30dB), this method can also be very accurate.
Y Factor Method
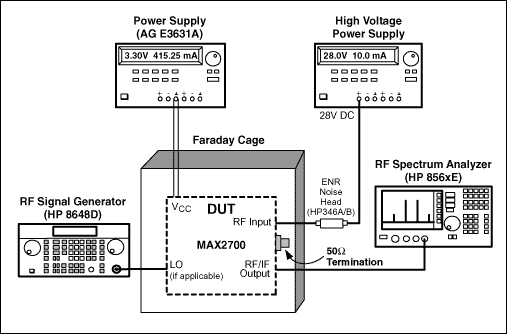
Y Factor method is another popular way to measure Noise Figure. To use the Y factor method, an ENR (Excess Noise Ratio) source is needed. It is the same thing as the noise source we mentioned earlier in the "Noise Figure Meter" section. The setup is shown in the Figure 3:
The ENR head usually requires a high DC voltage supply. For example, HP346A/B noise sources need 28VDC. Those ENR heads works are a very wide band (e.g.10MHz to 18GHz for the HP346A/B) and they have a standard noise figure parameter of their own at specified frequencies. An example table is given below. The noise figures at frequencies between those markers are extrapolated.
| HP346A | HP346B | |
| Frequency (Hz) | NF (dB) | NF (dB) |
| 1G | 5.39 | 15.05 |
| 2G | 5.28 | 15.01 |
| 3G | 5.11 | 14.86 |
| 4G | 5.07 | 14.82 |
| 5G | 5.07 | 14.81 |
Turning the noise source on and off (by turning on and off the DC voltage), an engineer measures the change in the output noise power density with a spectrum analyzer. The formula to calculate noise figure is:
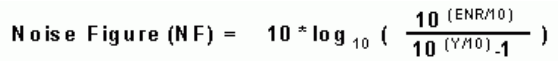
In which ENR is the number given in the table above. It is normally listed on the ENR heads. Y is the difference between the output noise power density when the noise source is on and off.
The equation comes from the following:
An ENR noise head provides a noise source at two "noise temperatures": a hot T = TH (when a DC voltage is applied) and a cold T = 290°K. The definition of ENR of the noise head is:
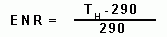
The excess noise is achieved by biasing a noisy diode. Now consider the ratio of power out from the amplifier (DUT) from applying the cold T = 290°K, followed by applying the hot T = TH as inputs:
Y = G(Th + Tn)/G(290 + Tn) = (Th/290 + Tn/290)/(1 + Tn/290).
This is the Y factor, from which this method gets its name.
In terms of Noise figure, F = Tn/290+1, F is the noise factor (NF = 10 * log(F))Thus, Y = ENR/F+1. In this equation, everything is in linear regime, from this we can get the equation above.
Again, let's use MAX2700 as an example of how to measure noise figure with the Y-factor method. The set up is show above in Figure 3. Connect a HP346A ENR noise head to the RF input. Connect a 28V DC supply voltage to the noise head. We can monitor the output noise density on a spectrum analyzer. By Turning off then turning on the DC power supply, the noise density increased from -90dBm/Hz to -87dBm/Hz. So Y = 3dB. Again to get a stable and accurate reading of the noise density, RBW/VBW is set to 0.3. From Table 1, at 2GHz, we get ENR = 5.28dB. Thus we can calculate the NF to be 5.3dB.
Summary
In this article, three methods to measure the noise figure of RF devices are discussed. They each have advantages and disadvantages and each is suitable for certain applications. Below is a summary table of the pros and cons. Theoretically, the measurement results of the same RF device should be identical, but due to limitations of RF equipment (availability, accuracy, frequency range, noise floor, etc), we have to carefully choose the best method to get the correct results.
| Suitable Applications | Advantage | Disadvantage | |
| Noise Figure Meter | Super low NF |
Convenient, very accurate when measuring super low (0-2dB) NF. | Expensive equipment, frequency range limited |
| Gain Method | Very high Gain or very high NF | Easy setup, very accurate at measuring very high NF, suitable for any frequency range | Limited by Spectrum Analyzer noise floor. Can't deal with systems with low gain and low NF. |
| Y Factor Method | Wide range of NF | Can measure wide range of NF at any frequency regardless of gain | When measuring Very high NF, error could be large. |
Related to this Article
Products
Direct-Conversion Tuner ICs for Digital DBS Applications
3.4GHz to 3.8GHz SiGe Low-Noise Amplifier/PA Predriver
1575MHz/1900MHz Variable-IP3 Low-Noise Amplifiers
3.5GHz Downconverter Mixers with Selectable LO Doubler
1.8GHz to 2.5GHz, Direct-Downconversion Receivers
5GHz Low-Noise Amplifier with Shutdown
300MHz to 2500MHz SiGe Ultra-Low-Noise Amplifiers
5GHz to 6GHz Low-Noise Amplifier in 6-Pin UCSP
1575MHz/1900MHz Variable-IP3 Low-Noise Amplifiers
300MHz to 2500MHz SiGe Ultra-Low-Noise Amplifiers
825MHz to 915MHz, SiGe High-Linearity Active Mixer
900MHz SiGe, High-Variable IP3, Low-Noise Amplifier
1575MHz/1900MHz Variable-IP3 Low-Noise Amplifiers
900MHz SiGe, High-Variable IP3, Low-Noise Amplifier