Abstract
Noise figure is routinely used by system and design engineers to ensure optimal signal performance. However, the use of mixers in the signal chain creates challenges with straightforward noise-figure analysis. This tutorial starts by examining the fundamental definition of noise figure and continues with an equation-based analysis of cascade blocks involving mixers, followed by typical lab techniques for measuring noise figure. This tutorial also covers the concepts of noise temperature and Y-factor noise measurement before exploring the use of the Y-factor method for mixer noise-figure measurements. Examples of double-sideband (DSB) and single-sideband (SSB) noise-figure measurements are discussed.
A similar version of this article appeared in the May 2013 issue of Microwave Journal.
Introduction
The general concept of noise figure is well understood and widely used by system and circuit designers alike. In particular, it is used to convey noise-performance requirements by product definers and circuit designers and to predict the overall sensitivity of receiver systems.
The principle difficulty with noise-figure analysis arises when mixers are part of the signal chain. All real mixers fold the RF spectrum around the local oscillator (LO) frequency, creating an output that contains the summation of the spectrum on both sides according to fOUT = |fRF - fLO|. In heterodyne architectures, one of these contributions is typically considered spurious and the other intended. Therefore, image reject filtering or image canceling schemes are likely to be employed to largely remove one of these responses. In direct-conversion receivers, the case is different; both sidebands (above and below fRF = fLO) are converted and utilized for the wanted signal. Consequently, this is truly a double-sideband (DSB) application of the mixers.
Various definitions commonly used in industry account for noise folding to varying degrees. For example, the traditional single-sideband noise factor, FSSB, assumes that the noise from both sidebands is allowed to fold into the output signal. However, only one of the sidebands is useful for conveying the wanted signal. This naturally results in a 3dB increase in noise figure, assuming that the conversion gain at both responses is equal. Conversely, the DSB noise figure assumes that both responses of the mixer contain parts of the wanted signal and, therefore, noise folding (along with corresponding signal folding) does not impact the noise figure. The DSB noise figure finds application in direct-conversion receivers as well as in radio astronomy receivers. However, deeper analysis shows that it is not sufficient for designers just to choose the right “flavor” of noise figure for a given application and then to substitute the corresponding number in the standard Friis equation. Doing so can lead to substantially faulty analysis, which could be particularly severe in cases when the mixers or components following the mixer play a non-negligible role in determining system noise figure.
This tutorial ties together the fundamental definition of noise figure, the equation-based analysis of cascade blocks involving mixers, and the typical lab techniques for measuring noise figure. In it, we show how the cascaded noise-figure equation is modified by the presence of one or more mixers, and we derive the applicable equations for a number of popular downconversion architectures. We then describe the Y-factor method of noise-figure measurement, using a mixer as the device under test (DUT). Using a mixer as DUT allows us to identify appropriate measurement methods for mixer noise figures that can be validly applied with the cascade equations.
Conceptual Model of Mixer Noise
One way to visualize mixer noise contributions is to consider a conceptual model of a mixer (Figure 1). This model is based on one provided by Agilent’s Genesys simulation program.1

Figure 1. Mixer noise contributions.
In this model, the input signal is split into two independent signal paths, one representing RF frequencies above the LO and the other representing frequencies below the LO. Each path is subject to independent additive noise processes in the mixer, and independent amounts of conversion gain are applied. Finally, the two paths are translated into the IF frequency and additively combined with further noise contributions that can arise in the output stage of the mixer. The self-noise power per unit bandwidth might not be the same in the wanted and image bands; the corresponding conversion gains might also be different.
For convenience, we can refer all the sources of noise to the output and collect them in a global noise term, NA, representing the total additional noise power per unit bandwidth available from the mixer output port.
NA = NSGS + NIGI + NIF
Note that NA is not at all dependent on the presence or absence of signals at the mixer’s input port.
Having summarized the internal noise sources of the mixer, we now turn to the noise attributable to the source termination (Figure 2). We identified two discrete noise sources representing the input noise density due to the source termination at the wanted frequency and the image frequency, respectively. We must account for these as independent quantities, because the application circuit can cause one of them to be attenuated and the other transferred with low loss to the mixer’s RF input port. This will likely be the case, if the image and wanted RF frequencies are well separated and a frequency-selective match is employed.

Figure 2. Source noise and mixer noise contributions.
In the case of a broadband match, we could write NOUT = NA + kT0GS + kT0GI. However, in the case of a high-Q, frequency-selective match to the mixer at the wanted RF frequency, the noise at the output due to the source termination at the image frequency is likely to be negligible, leading to NOUT = NA + kT0GS. Generally, we can assign a coefficient, α, to the effective fraction of the input source-termination noise power available to the mixer’s input port at the image frequency. Thus, NOUT = NA + kT0GS + αkT0GI, where α is an application-specific coefficient in the range 0 ≤ α ≤ 1. Later we shall see that the effective noise figure in an application depends on the value of α.
Noise-Figure Definitions
Before discussing why cascaded noise-figure calculations can be misleading, we should review some basic definitions of the term.
A reasonable starting point for explaining noise factor (F) for a two-port network is:
F = (SNRIN)/(SNROUT)
Which, when expressed in dB, is termed the noise figure (NF):
NF = 10log10(F)
This expression depends on the SNR of the input signal. If SNR is left undefined, however, this measure is meaningless as a performance measure of the circuit or component itself, since it largely depends on the quality of the signal feeding it. Therefore, it is desirable to assume the best-case scenario for the SNR at the input, namely that the only source of noise is due to the thermal noise of the input termination at some defined temperature. It is also logical to assume that the noise factor does not depend on the signal levels used. This assumes that the two-port network being characterized is in its linear operating region. This can be seen if we let the input signal power be PIN and the signal gain be Gs. Then, the output power is given by POUT = GsPIN and:

Furthermore, these noise powers, NINand NOUT, are ill-defined unless we specify the bandwidths in which they are measured. This can be solved by specifying NINand NOUTto represent noise power per unit bandwidth at any given specified input and output frequency.
Single-Sideband Noise Factor
The above considerations help to explain the rationale for the IEEE® definition of noise factor:
Noise Factor (Noise Figure) (of a Two-Port Transducer). At a specified input frequency the ratio of 1) the total noise power per unit bandwidth at a corresponding output frequency available at the output Port to 2) that portion of 1) engendered at the input frequency by the input termination at the Standard Noise Temperature (290K).
Note 1: For heterodyne systems there will be, in principle, more than one output frequency corresponding to a single input frequency, and vice versa; for each pair of corresponding frequencies a Noise Factor is defined.
Note 2: The phrase “available at the output Port" may be replaced by “delivered by the system into an output termination."
Note 3: To characterize a system by a Noise Factor is meaningful only when the input termination is specified.2
This definition of noise factor is a point function of output frequency, with respect to one corresponding RF frequency, not a pair of RF frequencies simultaneously, which is what makes it a single-sideband (SSB) noise factor (see Figure 3).

Figure 3. SSB noise figure.
It is important to note that the denominator only includes noise from one sideband; the numerator comprises the total noise power per unit bandwidth at a corresponding output frequency without making any specific exclusions. To make this explicit in mathematical form for the case of a mixer with signal and image responses, the above definition can be written as:

Where GIis the conversion gain at the image frequency; GSis the conversion gain at the signal frequency; T0 is the standard noise temperature; and NA is the noise power per unit bandwidth added by the mixer’s electronics as measured at the output terminals. The corresponding noise factor for the image frequency can be written as:

This is a different number if the conversion gain at the image frequency is different from that at the wanted signal frequency. There are some who interpret the IEEE definition above to exclude the image noise from the term “total noise power per unit bandwidth at a corresponding output frequency available at the output Port.”3 They therefore assume:

This definition corresponds to a situation where the source input noise at the image frequency is fully excluded from the mixer’s input port. This interpretation is not widely utilized by industry practitioners. Nevertheless, for the sake of completeness, it is illustrated in Figure 4.

Figure 4. IEEE variant of SSB noise figure.
The U.S. Federal Standard 1037C has the following definition of noise factor:
Noise figure (NF): The ratio of the output noise power of a device to the portion thereof attributable to thermal noise in the input termination at standard noise temperature (usually 290K). Note: The noise figure is thus the ratio of actual output noise to that which would remain if the device itself did not introduce noise. In heterodyne systems, output noise power includes spurious contributions from image-frequency transformation, but the portion attributable to thermal noise in the input termination at standard noise temperature includes only that which appears in the output via the principal frequency transformation of the system, and excludes that which appears via the image frequency transformation. Synonym noise factor.4
Since this more recent definition explicitly includes spurious contributions from image frequency transformation in the output noise power, the SSB noise factor can be written as previously suggested:

Let us consider the case where GS = GI. Then:

If we further consider the case where the mixer adds no noise of its own, NA = 0, then we are left with F = 2 or NF = 3.01dB. This corresponds to the statement that the SSB noise figure of a noiseless mixer is 3dB.
Double-Sideband Noise Factor
There are cases where the “principle frequency transformation of the system” is not applicable terminology; both responses are equally wanted and useful. Examples include radiometers and direct-conversion receivers. In a direct-conversion receiver, the LO frequency is at the center of the RF passband of the wanted signal; the two responses of the mixer comprise contiguous halves of the overall wanted signal spectrum. Figure 5 illustrates this case.

Figure 5. DSB noise figure.
Therefore, in such cases it makes sense to consider a DSB noise factor:

If we assume that Gs = Gi, then:
FDSB = 1 + (NA/(2kT0GS))
Under the same constraint:
FSSB = 2 + NA/(kT0GS)
This leads to the observation that, where both conversion gains are equal, the SSB noise figure of the mixer is 3dB higher than the corresponding DSB noise figure. Moreover, if the mixer does not add any additional noise (NA = 0), then FDSB = 1 or NFDSB = 0dB.
Use of Noise Figures in Cascaded Noise-Figure Calculations
Baseline Case: Cascade of Linear Circuit Blocks
Consider the following simple cascade of three amplifier blocks (Figure 6).

Figure 6. Three gain blocks cascaded.
The total noise at the output can be calculated as:
NOUT = kT0G1G2G3 + NA1 G2G3 + NA2G3 + NA3
The noise at the output that is attributable to the thermal noise at the input of the cascade is:
NOT = kT0G1G2G3
This implies that the overall noise factor is:

Substituting:
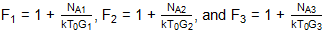
Yields:
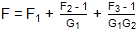
This can be recognized as the standard Friis cascade noise equation for three blocks. Extension to any number of blocks is trivial from here.
A Heterodyne Conversion Stage
Consider the following frequency conversion stage in a receiver signal path (Figure 7). The DSB noise figure of the mixer is 3dB and its conversion gain is 10dB. The wanted carrier frequency is at 2000MHz and the LO is chosen at 1998MHz, so that both the wanted and image frequencies are within the passband of the filter.

Figure 7. Heterodyne stage with no image rejection.
The cascaded performance of this arrangement is summarized in Table 1, where CF is the channel frequency, CNP is the channel noise power (measured in 1MHz bandwidth), gain is the stage gain, CG is the cascaded gain up to and including the present stage, and CNF is the cascaded noise figure.
| Parts | CF (MHz) | CNP (dBm) | Gain (dB) | CG (dB) | CNF (dB) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 |
| BPF_Butter_1 | 2000 | -113.975 | -7.12E-04 | -7.12E-04 | 6.95E-04 |
| BasicMixer_1 | 2 | -97.965 | 10 | 9.999 | 6.011 |
| *No image rejection from filter. | |||||
The overall cascaded gain of these two blocks is 9.999dB, while the SSB noise figure is 6.011dB. This noise figure could have been correctly anticipated from the previous analysis, since we expect the SSB noise figure to be 3.01dB higher than the DSB figure of the mixer. There is an additional very small noise figure degradation due to the finite insertion loss of the filter. Overall, this result meets our expectations.
Now we consider the same scenario, but with the LO frequency returned to 1750MHz (Figure 8). At this value of the LO frequency, the image is at 1500MHz, which is well outside the passband of the filter in front of the mixer.

Figure 8. Heterodyne stage with image rejection.
The cascaded performance of this arrangement is summarized in Table 2. The gain of the wanted signal is the same as before, but the cascaded noise figure (CNF) has changed to a value of 4.758dB.
| Parts | CF (MHz) | CNP (dBm) | Gain (dB) | CG (dB) | CNF (dB) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 |
| BPF_Butter_1 | 2000 | -113.975 | -7.12E-04 | -7.12E-04 | 6.95E-04 |
| BasicMixer_1 | 250 | -99.218 | 10 | 9.999 | 4.758 |
| *Significant image rejection from filter. | |||||
To explain this result, we need to consider that the noise situation in this scenario is similar to that depicted in Figure 4. Specifically, the source impedance image noise is suppressed. The added noise from the mixer stage can be calculated from the previously derived equation for the DSB noise factor:
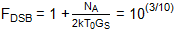
Therefore:
NA = 2kT0GS(10(3/10) - 1)
Now the total noise at the output of the mixer is given by NOUT = NA + kT0GS + αkT0GI, with α = 0 in this application. Thus:
NOUT = 2kT0GS(10(3/10) - 1) + kT0GS
The resulting noise figure can be written as:

Expressing this in dB, we have:
NF = 10log10(2(10(3/10) - 1) + 1) = 4.757dB
This should be compared to the simulated value of 4.758dB, which included a tiny additional contribution from the insertion loss of the filter.
In general, the effective SSB noise figure for the mixer stage is given by:
FSSBe = 2(FDSB – 1) + 1 + α
Where a = 0 for the case where termination noise at the image frequency is well suppressed, and α = 1 where it is not suppressed at all. Note that if α = 1, the effective single-side band (SSB) noise figure reduces to FSSBe = 2FDSB, which is the case illustrated at the beginning of this section. In some scenarios, fractional values of a can arise, e.g., if the image suppression filter is not directly coupled to the mixer input terminals or if the frequency separation between image and wanted responses is not large.
A Heterodyne Receiver
We can see how to apply the effective noise figure in larger cascade analysis with the example in Figure 9. To calculate the cascaded noise figure of the entire chain, we need to encapsulate the mixer and its associated LO and image reject filtering as an equivalent two-port network that has specific gain and noise figure. The effective noise factor of this two-port network is FSSBe = 2(FDSB – 1) + 1, since the termination noise at the image frequency is well suppressed by the preceding filter.

Figure 9. Heterodyne mixer in the context of adjacent system blocks.
Note that the applicable noise figure is neither the DSB nor the SSB noise figure of the mixer. Instead it is an effective noise figure that lies somewhere between these two values. In this case with a DSB noise figure of 3dB, the equivalent noise figure of the two-port network can be calculated to be 4.757dB, as already noted above. Using this value in the overall cascade calculation results in a system noise figure of 7.281dB, as shown in Table 3. Manual calculations show that this result is consistent with the standard Friis equation using 4.757dB for the mixer noise figure.
| Parts | CF (MHz) | CNP (dBm) | Gain (dB) | SNF (dB) | CG (dB) | CNF (dB) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 | 0 |
| Lin_1 | 2000 | -100.975 | 10 | 3 | 10 | 3 |
| BPF_Butter_1 | 2000 | -100.976 | -7.12E-04 | 7.12E-04 | 9.999 | 3 |
| BasicMixer_1 | 250 | -90.563 | 10 | 3 | 19.999 | 3.413 |
| Lin_2 | 250 | -61.695 | 25 | 25 | 44.999 | 7.281 |
In general, when substituting an equivalent two-port network for the mixer and its adjacent components, the input port should be the latest node in the signal flow for which the image response is rejected. The output port should be the earliest node where the image and wanted responses are combined together (usually the output port of the mixer). If the image response of the mixer is not effectively suppressed by the architecture, then the Friis equation cannot be used without modification.
A Zero-IF Receiver
Now consider a zero-IF (ZIF), or direct-conversion, receiver (Figure 10).

Figure 10. ZIF receiver with a low-noise amplifier (LNA), mixers, filters, and variable-gain amplifiers (VGAs).
This lineup consists of an LNA with 10dB of gain and 3dB noise figure; a bandpass filter centered at 950MHz; a signal splitter to send the signal to a pair of mixers, each with a conversion gain of 6dB; and a DSB noise figure of 4dB. The VGAs are defined to have a gain of 10dB and a 25dB noise figure. A simulation of this lineup produced the results shown in Table 4, where CP is channel power and SNF is stage noise figure. The other items are the same as in previous tables.
| Parts | CF (MHz) | CP (dBm) | CNP (dBm) | Gain (dB) | SNF (dB) | CG (dB) | CNF (dB) |
| MultiSource_1 | 950 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
| BasicMixer_1 |
0 | -67.039 | -99.425 | 5.979 | 4 | 12.959 | 3.81 |
| LPF1 | 0 | -67.04 | -99.425 | -8.23E-04 | 1.00E-02 | 12.958 | 3.81 |
| Lin_2 | 0 | -57.036 | -83.078 | 9.995 | 25 | 22.953 | 10.163 |
| LPF2 | 0 | -57.038 | -83.08 | -1.90E-03 |
1.00E-02 | 22.951 | 10.163 |
In Table 5 we show the results of calculations using the conventional Friis formula for cascaded noise figure. The main difference with Table 4, which shows results from a simulator, is in the final column, CNF.
| Parts | F (dB) |
Gain (dB) | CG (dB) | CNF (dB) |
| BPF filter | 0.01 | -0.01 | -0.01 | 0.01 |
| LNA | 3 | 10 | 9.99 | 3.01 |
| Splitter | 3.01 | -3.01 | 6.98 | 3.22 |
| Mixer | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 12.65 |
| LPF2 | 0.01 | -0.01 | 22.93 | 12.65 |
Clearly something has gone wrong with the cascaded noise figure. We are estimating 12.64dB using the spreadsheet, but the simulator is finding 10.16dB. The cascaded gains match reasonably well, but we need to establish which of the noise figures is valid. First, we are interested in the DSB noise figure of the entire structure, since the entire ZIF structure uses signals in both sidebands and suffers noise in both sidebands. Therefore, it is relevant to derive the DSB noise figure of a cascade involving an amplifier, followed by a mixer, followed by an additional amplifier (Figure 11).

Figure 11. Cascade including a mixer.
The total noise density at the output can be calculated as:
NOUT = 2kT0G1G2G3 + 2NA1G2G3 + NA2G3 + NA3
The noise at the output that is attributable to the thermal noise at the input of the cascade is:
NOT = 2kT0G1G2G3
This implies that the overall noise factor is:

Substituting:
F1 = 1 + NA1/(kT0G1), F2DSB = 1 + NA2/(2kT0G2), and F3 = 1 + NA3/(kT0G3)
Yields:
FDSB = F1 + (F2DSB - 1)/G1 + (F3 - 1)/(2G1G2)
This derivation indicates that it is necessary to use the DSB noise figure of the mixer in the cascade equation, and that the noise contributions from all following stages must be divided by 2 with respect to the usual form of the Friis equation for a cascaded noise figure. The failure to perform this latter division by 2 caused the spreadsheet equation analysis shown in Table 5 to be wrong. Amending the equations in the spreadsheet cells after the mixer to include the necessary division by 2 gives the result shown in Table 6.
| Parts | F (dB | Gain (dB) | CG (dB) | CNF (dB) |
| BPF filter | 0.01 | -0.01 | -0.01 | 0.01 |
| LNA | 3 | 10 | 9.99 | 3.01 |
| Splitter | 3.01 | -3.01 | 6.98 | 3.22 |
| Mixer | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 10.17 |
| LPF2 | 0.01 | -0.01 | 22.93 | 10.17 |
The agreement between Table 4 and Table 6 is now good. However, this exercise has also demonstrated the dangers of directly substituting into the Friis cascade equation where mixers are involved.
Next we consider the same scenario, but with the wanted signal 300kHz higher than the LO. The block diagram remains as illustrated in Figure 10, but all of the signal falls on the high side of the LO. This makes it a low-IF (LIF) application of the same receiver architecture. Using the same Genesys simulation workspace as before, the results are as shown below in Table 7.
| Parts | CF (MHz) | CP (dBm) | CNP (dBm) | Gain (dB) | SNF (dB) | CG (dB) | CNF (dB) |
| MultiSource_1 | 950.3 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
| BasicMixer_1 |
0 | -67.039 | -99.425 | 5.979 | 4 | 12.959 | 3.81 |
| LPF1 | 0 | -67.04 | -99.425 | -8.23E-04 | 1.00E-02 | 12.958 | 3.81 |
| Lin_2 | 0 | -57.036 | -83.078 | 9.995 | 25 | 22.953 | 10.163 |
| LPF2 | 0 | -57.038 | -83.08 | -1.90E-03 |
1.00E-02 | 22.951 | 10.163 |
These results are similar to the previous simulation of the same architecture, except that the noise figure has increased by 3dB. In fact, even if all the components of this system were noiseless, except the source resistance, the noise figure would be 3dB. Essentially, this is an SSB application of the complex receiver structure, and there are no measures to suppress the unwanted sideband. The derivation for the cascaded noise figure is identical to that already given, except that the output noise attributable to the thermal noise at the input of the cascade is once again:
NOT = kT0G1G2G3
So now:

Substituting:

Yields:

As expected, every term in the noise cascade equation is multiplied by 2, relative to the DSB use case of this structure. However, this situation is somewhat artificial. We now have a receiver that is wide open to both sidebands in terms of noise and interference, but it is only being used for signal in one of those sidebands. Since the lower sideband only contributes to the vulnerability of the receiver, it would make sense to employ the quadrature channel to provide rejection to the unwanted sideband. One solution would be to combine the I and Q signals at the output of the receiver with a 90 degree combiner, thus cancelling signals in the unwanted sideband while constructively adding them in the wanted sideband. This would, in effect, convert the entire receiver into an image reject downconverter. The final combining stage would recover the system noise figure by the 3dB previously lost, assuming that the phases of the signals being combined were sufficiently well controlled at the combining point. A simulation schematic for such a scheme is shown in Figure 12 and the corresponding results are tabulated in Table 8.

Figure 12. Near ZIF receiver with image rejection.
| Parts | CF (MHz) | CP (dBm) | CNP (dBm) | Gain (dB) | SNF (dB) | CG (dB) | CNF (dB) |
| MultiSource_1 | 950.3 | -79.995 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.005 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950.3 | -70.004 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950.3 | -73.014 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
| BasicMixer_1 |
0.3 | -67.053 | -96.441 | 5.958 | 4 | 12.938 | 6.815 |
| LPF1 | 0.3 | -67.005 | -96.443 | -1.64E-03 | 1.00E-02 | 12.936 | 6.815 |
| Lin_2 | 0.3 | -57.047 | -80.09 | 9.991 | 25 | 22.927 | 13.177 |
| LPF2 | 0.3 | -57.051 | -80.094 | -3.82E-03 |
1.00E-02 | 22.923 | 13.177 |
| Split290_2 | 0.3 | -54.062 | -80.145 | 3.001 | 3.02 | 25.923 | 10.125 |
The improvement of the cascaded noise figure (CNF) by 3dB at the final (combining) stage shows the restoration of the noise figure, as expected.
The use of Agilent® Genesys to simulate these architectures and scenarios has proven to agree with mathematical derivations of the appropriate cascaded noise figure in the cases examined.
For each architecture discussed and simulated, the cascaded noise factor equation is summarized in Table 9.
| Structure | Application | Cascaded F Equation |
| Three gain blocks | Any |  |
| Heterodyne mixer | SSB, ideal image filtering |  |
| Complex downconverter | ZIF |  |
| Complex downconverter | LIF, no image suppression |  |
| Complex downconverter | LIF, image reject combining |  |
Noise Temperature
To discuss Y-factor noise measurement, it is necessary to introduce the concept of noise temperature. In previous equations, we used the well-known result that noise-power spectral density available from a resistor at a given temperature is kT, W/Hz, where k is Boltzmann’s constant and T is the absolute temperature. This makes it possible to account for all sources of noise in a device, if we pretend that the device is noiseless and if the additional noise-power spectral density is accounted for by an equivalent rise in noise temperature of the input termination above the reference temperature. The noise factor can be related to the equivalent temperature, Te, by F = 1 + Te/T0, where T0 is defined as the reference noise temperature of 290K. Unsurprisingly, a noise factor of 1 is represented by an equivalent noise temperature of the device of 0K, whereas a noise factor of 2 is represented by Te = 290K.
Y-Factor
The Y-factor method for noise-figure measurement5 involves the use of a calibrated noise source, which has two distinct noise temperatures depending on the presence or absence of DC power to the device. The calibrated source has a characterized excess noise ratio (ENR) defined as:
ENRdB = 10log10 [(TSON - TSOFF)/T0]
Where TSON is the noise temperature of the source in its ON state and TSOFF is the corresponding value in its OFF state. The Y-factor is a ratio of two noise power levels, one measured with the noise source ON and the other with the noise source OFF.
Y = NON/NOFF
Since the noise power available from a source can be represented directly by its noise temperature, we can also write:
Y = TON/TOFF
Noise-Factor Measurement and Calculation
To assess the noise factor of a DUT, we must connect a noise-power measurement device to the output of the DUT. Let the DUT have a noise temperature T1 and the instrument have a noise temperature T2. While it is impossible to eliminate the measurement device’s noise temperature (T2) from any given reading, we can measure T12, which is the combined noise temperature of the DUT followed by the instrument. We can use calculations to isolate T1 since T12 = T1 + T2/G1. So, the strategy is to take a Y-factor measurement with the calibrated noise source connected directly to the measuring instrument, which will allow T2 to be determined. We have:
Y2 = N2ON/N2OFF = (TSON + T2)/(TSOFF + T2)
Which can be rearranged as:

Having obtained the noise temperature of the measuring device, based on known values of TSON and TSOFF, the next step is to measure a new Y-factor for the cascade of the DUT and the measuring instrument:
Y12 = N12ON/N12OFF
This allows the combined noise temperature of the DUT and the instrument to be calculated using the same procedure as before:
T12 = (TSON - Y12 TSOFF)/(Y12 - 1)
Having previously stored both N1ON and N1OFF and now having access to N12ON and N12OFF, we have sufficient information to calculate the gain of the DUT as:
G1= (N12ON - N12OFF)/(N2ON - N2OFF)
This provides sufficient information to mathematically subtract the contribution of the measuring instrument’s noise temperature using:
T1 = T12 - T2/G1
Losses Before the DUT
If there are known losses before the DUT, the impact of these losses must be removed to obtain the true noise temperature of the DUT at its input T1IN. Assuming that these losses are absorbative, the following equation can be used:
T1IN = (T1/LIN) - ((LIN - 1)TL/LIN)
Where TL is the physical temperature of the loss and LIN is the insertion loss to be compensated, which is expressed as a linear power ratio greater than unity.
Mixer as DUT in the Y-Factor Noise-Factor Determination
Consider that the calibrated noise sources used for noise-figure measurement are broadband in nature and that any slight variation in noise temperature when ON is handled by a detailed calibration table embedded in the source. As a result, any unmodified use of the Y-factor technique results in the evaluation of the DSB noise figure of the mixer. This is because the calibrated noise source injects noise power in both sidebands simultaneously, and the combined output noise power from both sidebands contributes to the output noise temperatures used to calculate the Y-factor. Two example cases given below illustrate how the measurement method can be used with and without modification to obtain DSB or SSB measurements, respectively.
Example of the DSB Noise-Figure Measurement by the Y-Factor Method
To illustrate the concepts discussed, an Agilent Genesys simulation is performed by injecting a noise source into the simulated DUT, which is a mixer with a DSB noise figure of 4.9dB and a conversion gain of 8.8dB. The noise power injected is determined by the variable PIN, which is a swept variable that iterates over two possible values, -159dBm/Hz and -174dBm/Hz, representing the ON and OFF conditions of the noise source, respectively. The IF is defined to be 250MHz with wanted and image responses at 2000MHz and 1500MHz in the RF port of the mixer (Figure 13). The only data collected by the simulation (Tables 10 and 11) are the channel noise power in 100kHz bandwidth both at the input (directly connected to the noise source in lieu of a calibration step) and at the output (representing the measurement mode).

Figure 13. Simulation schematic to determine the DSB mixer noise figure using the Y-factor method.
| B (Hz) | IL (dB)* | pinOFF (dBm) | pinON (dBm) | poutOFF (dBm) | poutON (dBm) |
| 100,000 | 0 | -123.975 | -109 | -107.265 | -96.91 |
| *Note that the parameter IL represents the insertion loss before the DUT, which in this case is 0dB. | |||||
| Y2 | Y12 | T12 (K) | T2 (K) | T1 (K) | T1IN (K) | F (dB) | G (dB) |
| 31.443 | 10.851 | 606.147 | 0 | 606.147 | 606.147 | 4.9 | 8.8 |
Note that T2 represents the noise temperature of the instrument, which is acceptable, since the instrument is, in this case, the Genesys simulator, which evaluates noise without adding any of its own. Because the insertion loss before the DUT is 0dB, T1 is identical to T1IN. The final calculated noise figure from the Y-factor measurements is given by F = 10log10 (1 + T1IN/290). The value obtained (4.9dB) aligns with the expected value from the parameter settings used when setting up the mixer schematic.
Example of SSB Noise-Figure Measurement by the Y-Factor Method
The simulation schematic is shown in Figure 14 and the test results in Tables 12 and 13.

Figure 14. Simulation schematic to determine the SSB mixer noise figure using the Y-factor method.
| B (Hz) | IL (dB)* | pinOFF (dBm) | pinON (dBm) | poutOFF (dBm) | poutON (dBm) |
| 100,000 | 2.2 | -123.975 | -109 | -108.015 | -101.455 |
| *Note that the parameter IL represents the insertion loss before the DUT, which in this case is 2.2dB. | |||||
| Y2 | Y12 | T12 (K) | T2 (K) | T1 (K) | T1IN (K) | F (dB) | G (dB) |
| 31.443 | 4.529 | 2211.584 | 0 | 2211.584 | 1217.354 | 7.158 | 6.602 |
Because the insertion loss before the DUT is 2.2dB, T1 is higher than the mixer’s noise temperature T1IN, which has been calculated according to Equation 42 in the Losses Before the DUT section. The final calculated noise figure from the Y-factor measurements is given by F = 10log10 (1 + T1IN/290). The value obtained is 7.158dB. This value should be compared to the value obtained with Equation 43, assuming that the image noise of the source is completely suppressed:
NF = 10log10 (2(10(4.9/10) - 1) + 1) = 7.144dB
Since the filter has finite insertion loss, the impedance of the image suppression filter at the image frequency is not entirely reactive. This, in turn, implies that the image-band noise of the source is not fully suppressed, which is assumed to be the cause of the small increase from the ideal noise figure.
Example of the SSB Noise-Figure Measurement by the Padded Y-Factor Method
In this method, we apply an attenuator to ensure that the mixer is subject to similar “cold” (i.e., OFF-state) noise temperatures at both the wanted and image frequencies. This should result in the SSB noise figure more closely approximating a value 3dB higher than the DSB noise figure, since the noise temperature of the source termination is no longer colored by the filter to any significant extent (Figure 15, Tables 14 and 15).

Figure 15. Simulation schematic to determine the SSB mixer noise figure using the padded Y-factor method.
| B (Hz) | IL (dB)* | pinOFF (dBm) | pinON (dBm) | poutOFF (dBm) | poutON (dBm) |
| 100,000 | 12.2 | -123.975 | -109 | -107.272 | -106.141 |
| *Note that the parameter IL represents the insertion loss before the DUT, which in this case is 12.2dB and represents the combined loss of the filter and attenuator. | |||||
| Y2 | Y12 | T12 (K) | T2 (K) | T1 (K) | T1IN (K) | F (dB) | G (dB) |
| 31.443 | 1.297 | 29392.313 | -5.98E-14 | 29392.313 | 1498.536 | 7.901 | -3.398 |
The final calculated noise figure from the Y-factor measurements is given by F = 10log10 (1 + T1IN/290). The value obtained is 7.901dB. This value corresponds well to the value that would be anticipated from adding 3.0dB to the DSB noise figure of 4.9dB. Note that the use of a 10dB attenuator causes the Y-factor to get close to unity, which might endanger accuracy. When using high values of attenuation in a real-world measurement, it is advisable to select the highest ENR source available to maintain accuracy.
Conclusion
In this tutorial, we saw that where a mixer is part of a receiver cascade, the Friis equation for cascaded noise factor is not usually valid using either the DSB or SSB versions of the mixer noise figure. In cases where a filter is used to largely remove the image response of the receiver, an equivalent two-port network can be substituted for the mixer, filter, and LO subsystem. However, the resultant noise figure must be calculated from the DSB noise figure, taking into account the frequency selectivity of the source termination coupled to the mixer’s input port.
We have also found that the same physical structure can have a different effective noise figure, depending on whether the signal is distributed around the LO or is entirely on one side of it (i.e., the application is DSB or SSB, respectively). The 3dB loss in SNR caused by using a complex receiver in LIF mode can be (and usually is) recovered by appropriate use of image reject combining, complex filtering, or equivalent baseband processing.
The Y-factor measurement evaluates the DSB noise figure of a mixer unless special actions are taken to filter out the broadband noise stimulus at the image frequency. This is the appropriate value to be used with the cascade equations derived previously. When a filter is used in an attempt to obtain the SSB noise figure, it is necessary to account for the insertion loss of the filter used. Furthermore, the degree of source termination image-noise suppression by the filter can cause a deviation from the classical definition of SSB noise figure. Use of a matched attenuator can overcome this problem to a large extent, providing that the amount of attenuation used is not excessive compared to the ENR of the noise source.
References
- For more information on Agilent’s mixer thermal noise model, see http://edocs.soco.agilent.com/display/genesys2010/MIXER_BASIC.
- “IRE Standards on Electron Tubes: Definitions of Terms, 1957,” Proceedings of the IRE, vol. 45, pp. 983–1010, July 1957; http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4056638&isnumber=4056624.
- Maas, S., Microwave Mixers, Artech House Microwave Library, Artech House, 1993.
- “Telecommunications: Glossary of Telecommunication Terms,” Federal Standard 1037C, June 1991; www.its.bldrdoc.gov/fs-1037/fs-1037c.htm.
- “Noise Figure Measurement Accuracy—The Y-Factor Method,” Agilent Technologies, Application Note 57–2, 2010; http://cp.literature.agilent.com/litweb/pdf/5952-3706E.pdf.
Related Parts
| LNA Application | Part Number | Description/Features | Key Specifications |
| GPS/GNSS | MAX2686L | LNA with integrated LDO | NF = 0.88dB, Gain = 19dB |
| AM/FM Radio | MAX2180A | Variable-gain LNA for active antenna applications | Integrated power detector and antenna sense |
| WLAN | MAX2692 | LNA with integrated 50Ω output matching circuit | NF = 1.1dB, Gain = 18.2dB |
| RKE | MAX2634 | Optimized for 315MHz to 433.92MHz remote keyless entry | NF = 1.2dB, IIP3 = -16dBm |
| HSPA/LTE | MAX2668 | Three programmable gain stages optimize linearity and sensitivity | NF = 1dB, Gain = 14.5dB |
| Gain Block | MAX2612–MAX2616 | 40MHz to 4GHz broadband operation with 0.5dB gain flatness | NF = 2.1dB, OIP3 = +35.2dBm |
| Mixer Type | Part Number | Description/Features | Key Specifications |
| Down Conversion High Linearity | MAX19998 | High linearity mixer with integrated LO buffer and power/performance bias | RFIN = 2GHz to 4GHz, IIP3 = 24.3dBm, 2RF - 2LO = 67dBc |
| Up/Down Conversion High Linearity |
MAX2042A | Ultra-wide LO frequency range supports low-side or high-side LO injection | RFIN = 1.6GHz to 3.9GHz, IIP3 = 33dBm, 2RF - 2LO = 72dBc |
| Down Conversion Broadband Low Power | MAX2680/MAX2681/MAX2682 | Miniature low noise mixer, low voltage operation, and low operating current | RFIN = 400MHz to 2.5GHz, IIP3 = -1.8dBm |
| Up Conversion Broadband Low Power |
MAX2660/MAX2661/MAX2663 MAX2671/MAX2673 |
Miniature low noise mixer, low voltage operation, and low operating current | RFIN = 400MHz to 2.5GHz, OIP3 = 9.6dBm |
| VCO/PLL Type | Part Number | Description/Features | Key Specifications |
| Fraction-n/Integer-n Synthesizer | MAX2870 | Ultra-wideband PLL with integrated VCO and integrated dividers | 23.5MHz to 6000MHz frequency range, -226.4dBc/Hz noise floor |




















