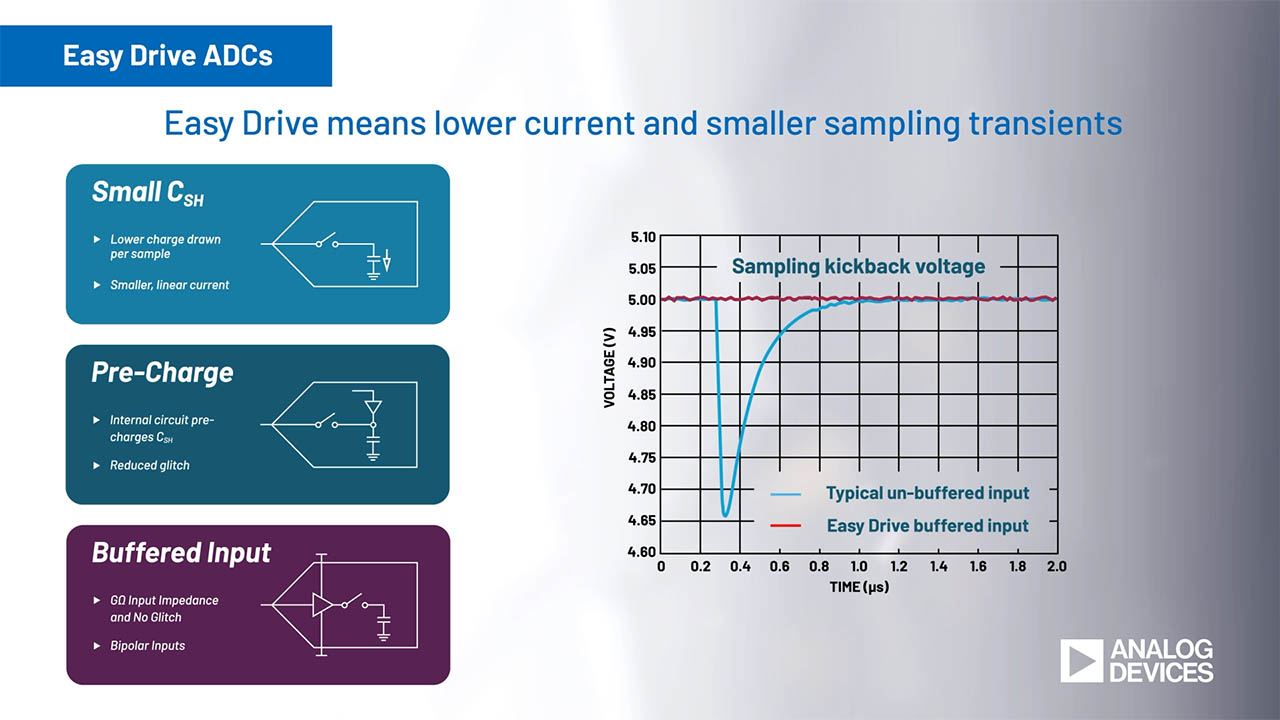
High Speed ADC Sampling Transients
High speed analog to digital converters (ADCs) are, at the analog signal interface, track and hold devices. As such, they include sampling capacitors and sampling switches. The action of these elements as they alternately track the input signal and hold its voltage produces small transient voltages and currents. These transients can introduce distortion into the circuitry that drives the ADC analog input.
High resolution ADCs are particularly susceptible to these effects. Consider a typical 16-bit ADC with a 2V peak to peak input range. The analog input voltage change required to affect the digital output by one bit is on the order of 30µV.
These high performance converters are almost always differential input devices, but the analysis here starts with a single-ended circuit model to show the transient effects. The degree to which these effects appear in a true differential setting depend heavily on the common mode rejection ratio of the signal source driving the ADC and the ADC itself.
Input Track and Hold Model
The input circuit to implement the track and hold function is shown in Figure 1. This is a simplified model, but it serves to illustrate the charge transfer effects that can distort the input waveform.

Figure 1. Track and hold model for single-ended signal.
There are three CMOS switches, a sample capacitor and an op amp. The circuit is driven by a sample clock, which can operate at 100MHz or more. It alternates between two phases: the track phase, in which the input analog voltage is placed onto a sample capacitor, and the hold phase, which disconnects the sample capacitor from the analog input and makes the capacitor voltage available to the digital circuitry that quantizes it. One edge of the sample clock—say the rising edge—initiates the track phase, and the next edge—say the falling edge—initiates the hold phase.
Note that the transition from the track phase to the hold phase is comprised of two transition states. The transition states exist because the three switches change state in sequence—not all at once. The transition from track phase to hold phase, along with the transition states, is shown in Figure 2. Note the directions of the transient currents on the sample and switch capacitances. In some cases the current changes direction as the switch control voltage ramps up/down.

(a) track phase

(b) transition state 1

(c) transition state 2

(d) hold phase
Figure 2. The transition from track phase to hold phase via transition states.
During the transition from track to hold phase, transient charges can be imposed on the sample capacitor, altering the final voltage on this capacitor at the beginning of the hold phase. The reason for these errant charges is the inherent channel capacitance of the CMOS switch. Each of the three CMOS switches includes a parasitic capacitance from gate to channel. When the control voltage on the switch changes, a small amount of charge is transferred to the channel.
In the track phase, the conditions are:
- Switches SW1 and 2 are closed; the control voltage on these switches is 1.8VDC. The channel capacitances of the switches are charged to 1.8V.
- Switch SW3 is open; the control voltage on this switch is zero volts DC. The channel capacitance of this switch is charged to zero volts.
Here is the sequence of events that make up the transition from track to hold phase:
- The control voltage VC1 for SW1 ramps to zero volts DC.
- The voltage at Node B is pulled lower by the charge on SW1.
- Some of the charge on the channel of SW1 flows to the sample capacitor; the effect is to increase the charge on the sample capacitor.
- The voltage across the sample capacitor increases.
- The control voltage VC2 for SW2 ramps to zero volts DC.
- The voltage at Node A is pulled lower by the charge on SW2.
- Some of the charge on the channel of SW2 flows to the sample capacitor; the effect is to decrease the charge on the sample capacitor.
- The voltage across the sample capacitor decreases.
- The control voltage VC3 for SW3 ramps to 1.8VDC.
- The voltage at Node A is pulled higher by the channel capacitance of SW3.
- The voltage across the sample capacitor increases.
- At the end of this sequence, the charge, and hence the voltage, on the sample capacitor has changed.
Time Domain Modeling
The time domain behavior of a typical input track and hold circuit can be modeled in PSPICE. Here are the assumed parameters:
- Input signal = 5MHz sine wave, 1V peak
- Sample capacitance = 2pF
- Switch channel capacitance = 0.2pF
- Switch control voltages = 0V/1.8V
- Switch ramp time = 100ps
The effects of the switching events are more evident if the three events are separated by 2ns each. Figure 3 shows each of the switching events, starting with switch SW1 opening at 5ns. At 7ns, SW2 opens; SW3 closes at 9ns. Note that once the tracking phase is complete, the op amp output voltage matches that of the sample capacitor. This voltage, however, differs from the input voltage because of the charge injected by the switches.

Figure 3. End of tracking phase, with switch parasitics.
Input Network Effects
The input network that links the analog signal source to the ADC input contributes to the transient charge effects outlined above. In particular, elements that store charge, or delay the transit of charge, can produce additional artifacts as the switches change state. Generally the input network consists of a driver amplifier, a simple RC network—usually lowpass—and some length of transmission line. Some length of transmission line is unavoidable, particularly as ADC packages become smaller. Simply conveying the input signal, which is always differential, from the discrete network to the ADC input pins involves distance. So a differential transmission line structure is used.
Examination of these artifacts in Figure 4 shows the transients imposed upon the input signal. In this case the input network consists of a pi section RC lowpass and a 200ps transmission line. The input signal shows the initial transient once SW1 opens, and echoes of this transient appear at 400ps intervals. Less evident but still present are the transients and their echoes on the sample capacitor. Note that if the switch events are separated enough in time for the transients to settle out before entering the hold phase, their effect on the final sample capacitor voltage decays to zero. Figure 5 shows these transients on the sample capacitor voltage in greater detail.

Figure 4. End of tracking phase, with switch parasitics, RC network and 200ps transmission line.

Figure 5. Detail of transients on the sample capacitor voltage.
In practice the three switch events are separated not by 2ns, but by 100ps or so. In this short window, transients have little time to decay before the last switch is closed and the voltage on the sample capacitor is captured. This gains importance with regard to the echoes from the transmission line structure. Figure 6 shows this behavior.

Figure 6. Fast switch behavior.
The transients on the sample capacitor are shown in detail in Figure 7. It has been shown that charge injection from the sample switches affects the final charge stored on the sample capacitor. This is a classic issue with track and hold circuits. We have also seen that settling transients can further affect this final charge, and hence the voltage passed on to the digital quantization portion of the ADC for that sample.

Figure 7. Detail of transients on the sample capacitor with fast switch events.
Multiple Sample Effects
Thus far we have examined the effect of these artifacts upon a single sample. The next step is to expand the field of view to see how the sample capacitor voltages differ from the input voltages at several sample instants. Figure 8 illustrates this. The input signal is a 1MHz sine wave, and the sample rate is 20Msps. The end of each track phase is denoted by a blue dashed vertical line. The error voltage on the sample capacitor is defined as the difference between the sample capacitor voltage and the input signal voltage.

Figure 8. Sample capacitor values vs source voltages.
The real error of interest consists of the difference between the sample capacitor voltage at the end of the hold phase and the input voltage at the end of the track phase. A set of these error samples has been plotted for one signal cycle and plotted in Figure 9. Note that the deviation from true input signal values is a time-varying quantity; it does not represent a DC offset that can be removed or ignored. It appears, most likely, as multiple harmonic and spurious signals in the digitized ADC output.

Figure 9. Error voltage at sample instants.
Common Mode Versus Differential Mode
Having explored all of this, there is an important factor that greatly reduces the effect of these transients on the output signal. This factor is the common mode rejection of the ADC. The ADC input is differential, and accepts a differential input signal. The switch effects, however, are not differential; they are the same on both sides of the input circuit. Since all of the switch charge transfers are common mode, they are rejected by the ADC. So the net effect of these distortions on the digitally represented output signal depends not only upon the magnitude of the errant charges, but also on the common mode rejection of the ADC.
Conclusion
The track and hold circuit at the input of an ADC necessarily injects transient charges into the circuit that drives it. These charges can affect the accuracy of the voltage stored on the sample capacitor at each sample instant. The key interval is the time it takes to transition from the track phase to the hold phase. During this time switches are toggled and the voltage stored on the sample capacitor can be perturbed.
Fortunately the ADC input is typically differential and the undesired transients are common mode. Nevertheless, any input circuit elements that store large amounts of charge, or cause charge to bounce back and forth will exacerbate the charge disturbances. The latter effect is usually the result of transmission line structures whose round trip delay falls within the transition time between the track and hold phases. In particular, if there are circuit elements at the input end of the line that are reflective relative to the transmission line, these contribute to the magnitude of the reflections.
All of the preceding modeling was done using LTspice and a simple input circuit model. There is no practical way to estimate the magnitude or spectral distribution of the distortions outlined, but the analysis suggests that minimizing the storage and reflection of transient charges will reduce them.
关于作者
现在他为各种SAR和Σ-Δ模数转换器提供应用支持。他的工作...
关联至此文章
{{modalTitle}}
{{modalDescription}}
{{dropdownTitle}}
- {{defaultSelectedText}} {{#each projectNames}}
- {{name}} {{/each}} {{#if newProjectText}}
-
{{newProjectText}}
{{/if}}
{{newProjectTitle}}
{{projectNameErrorText}}