摘要
本文详解控制理论。通常我们在讲解控制理论时,都只通过框图,而不参考实际的电路。在数学和电路仿真工具的帮助下,我们将一步步说明电子控制理论与现代电路设计息息相关。
简介
大学教授的许多科目都会令学生发问:"学习这门课程能让我找到一份工作吗?"控制理论可能就是这样一门课程,这些多达数页的数学和框图不会在实际电路中被直接使用。但是,控制系统教授工程师如何设计自动系统、系统距离实现稳定操作还有多大距离,以及如何从给定系统获得较佳响应。因为不管课程是关于机械、电气、土木、航空,或者是通信工程,如果系统不稳定,一切都没有用。
对于设计工程师来说,控制理论就是生命本身。
现在有许多关于控制理论的优秀文章,但是其中很多都是借助框图,以最概括化的方法来进行介绍。本文主要面向电子工程师,从电路分析和仿真的角度介绍电子控制系统;介绍了常见的二阶系统背后的理论,而且是利用有效的电路示例来加以说明;旨在揭露二阶系统的基础原理,并向尝试了解电子控制理论的人员说明,该理论与模拟电路设计之间存在关联。
二阶系统
图1所示为最基础的二阶网络。
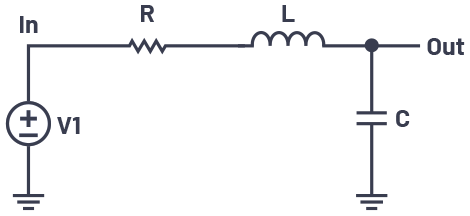
其传递函数为:

方程1右侧的分母被称为 特征多项式 ,如果我们令特征多项式为0,我们会得出特性方程。当转换函数的分母等于0时,得到系统的极点通过求解特性方程的根(让特性方程等于0的s的值),我们可以找到系统的极点,从而获取与系统运行状况相关的许多信息。
二阶系统传递函数的一般形式为:

其中ζ表示阻尼系数,ωn表示电路的固有振荡频率(或无阻尼频率),单位为弧度/秒。
所以,二阶系统的一般特性方程为:

比较方程3和方程1,我们可以看出,图1中的电路的固有频率为:

我们也可以看出,电路中的电阻会影响网络的阻尼系数:

所以

所以

可以直观看出,如果电路中没有电阻,网络不会出现耗损(无阻尼),如果模拟这种电路,则电路会永久振荡。随着电阻增加,振荡会更快衰减。
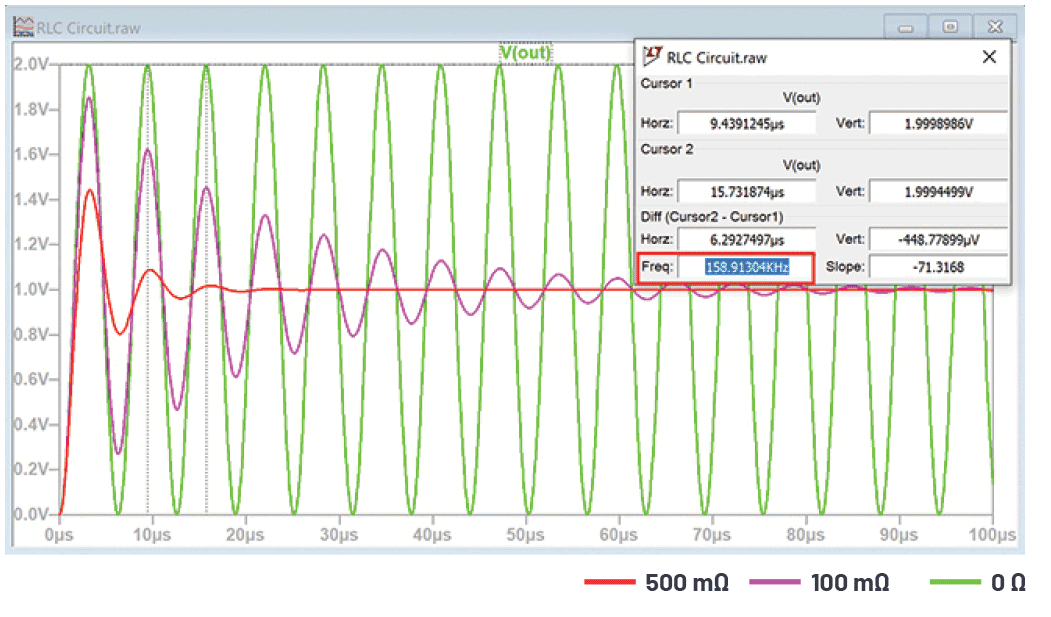
图2显示一个RLC电路,其中阶跃输入为1 V,L = 1 µH,C = 1 µF,电阻分别为0 Ω、100 mΩ和500 mΩ。电路按照预期的159 kHz频率振荡。电阻增加对衰减的影响一目了然。
我们可以通过将拉普拉斯域转换为时域,以数学方式展示图2所示的模拟结果。拉普拉斯域中的单位阶跃输入写为:

所以当我们使用单位阶跃输入仿真二阶系统时,结果会变成:
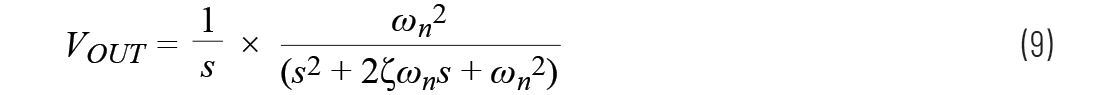
如果使用部份分式分解法,方程9可以写为:
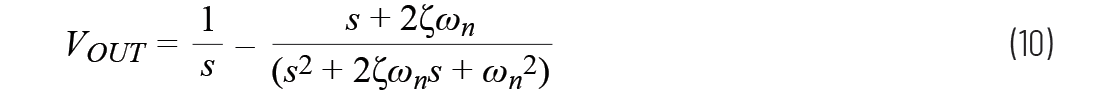
方程10是表示在拉普拉斯域中的。
在时域中,这会转换为:
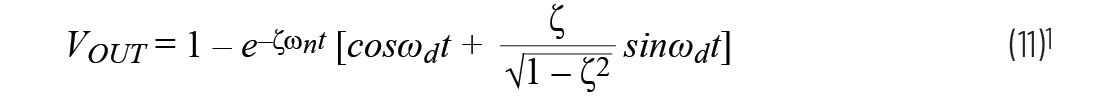
其中

采用逆拉普拉斯变换的公式11的数学推导如 附录A所示。
通过公式11,我们可以看出图1的电路如何响应阶跃输入。我们可以看到,波形具有与正弦曲线类似的特性,其幅度则由e–ζωnt项调制,根据阻尼系数是正数或复数出现指数式衰减或增加。近似来看,响应由正弦部分和余弦部分组成,但是,阻尼系统较低时,正弦部分非常小。
此外,尽管电路的固有频率为ωn,但电路不会按照此频率振荡,而是按照更低一些的频率ωd振荡,这个频率由阻尼系统ζ决定。这个频率被称为阻尼固有频率。然而,指数式衰减由电阻的无阻尼固有频率ωn决定。
要找出转换函数的极点,则需要确定转换函数何时等于0,也就是说:

s的值可以使用二次方程求解:

其中
a = 1
b = 2ζωn
c = ωn2
要得出系统极点,需要:

如果阻尼系数小于1,会得出负的平方根,所以最好将方程15写作:

我们之前说过 ωd = ωn√(1 – ζ2),所以方程16可以改写为:

这里我们可以看出,系统的极点包含实数部分(–ζωn)和虚数部分(±jωd)。
方程17可以求解得出特性方程的根(系统的极点)。我们如何将这些极点与系统的稳定性联系起来?现在我们需要把拉普拉斯域的极点和时域的稳定性联系起来。
通过方程11和方程17,我们可以得出以下观察结果。
无阻尼固有频率ωn决定了:
- 拉普拉斯域(方程17)中的极点(–ζωn)的虚数部分。
- 振荡的实际频率
由此,可以合理假设极点的虚数部分确定了系统振荡的实际频率。
这两个假设可以用s平面图表示,我将在下一节详细介绍。
稳定的系统
控制理论认为,如果极点位于s平面的左半部分,则系统是稳定的。图3所示为一个s平面示例,其中实数部分在x轴上绘制,虚数部分在y轴上绘制。
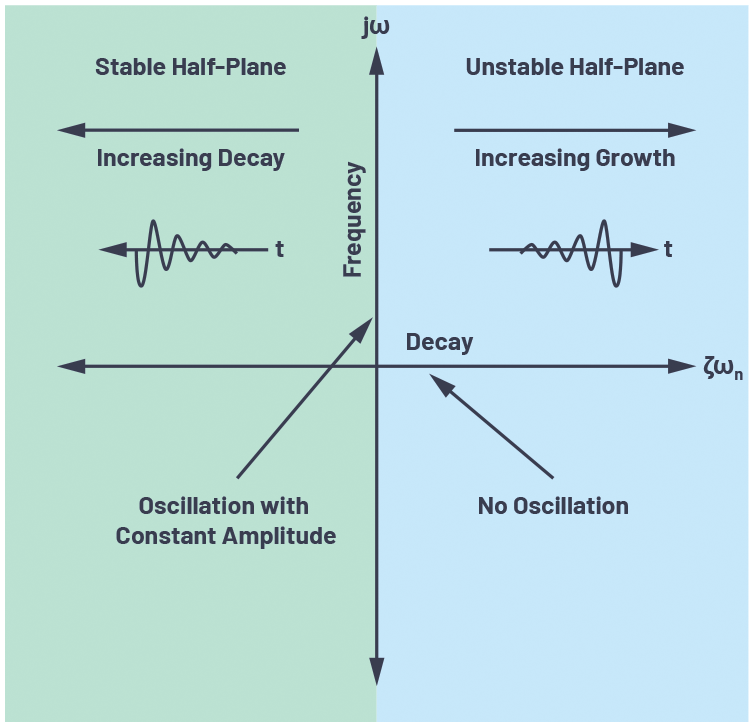
从方程17可以看出,如果阻尼系数为正(方程17的实数部分为负),则极点位于左半部分。随着阻尼系数增加,方程17的极点进一步向左移动(在左侧平面内,越来越靠近左侧)。
如果方程17在拉普拉斯域中,如何在时域中转换?
为了方便起见,我们再次使用方程11:
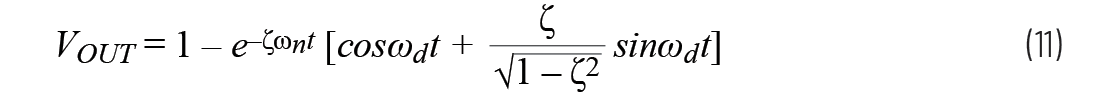
正阻尼系数ζ会引发指数式的衰减幅度响应(由e–ζωnt项表示),阻尼越大,衰减越快。随着阻尼系数增加,极点进一步向左移动(在拉普拉斯域内),这进一步增大了时域内的指数式衰减。从图2中可以看出这一点,图2使用100 mΩ和500 mΩ线路来表述电阻对阻尼的影响。在此区域中,500 mΩ线路的阻尼系数最大,所以它的指数式衰减最明显。0 Ω时,阻尼系数为0,此时极点完全位于y轴上,电路无限振荡,如图2中的绿色线路所示。
值得注意的是,即使系统是稳定的,这并不表示一定没有振荡。电路可能会在左半平面的极点处振荡,但是这些振荡的振幅会随着时间而衰减,如图2所示。
这对图1中的电路意味着什么?
我们知道图1中的阻尼是通过下方的方程得出:

它的固有频率则是:

所以,在L = 1 µH,C = 1 µF时,固有频率为1 Mrads–1 (= 159.1 kHz),R = 500 mΩ时的阻尼系数为0.25。
所以,阻尼振荡频率ωd由以下方程计算得出:

所以,阻尼振荡频率为968 krads–1,即154 kHz。这可以通过查看图4中红色波形的频率来说明。
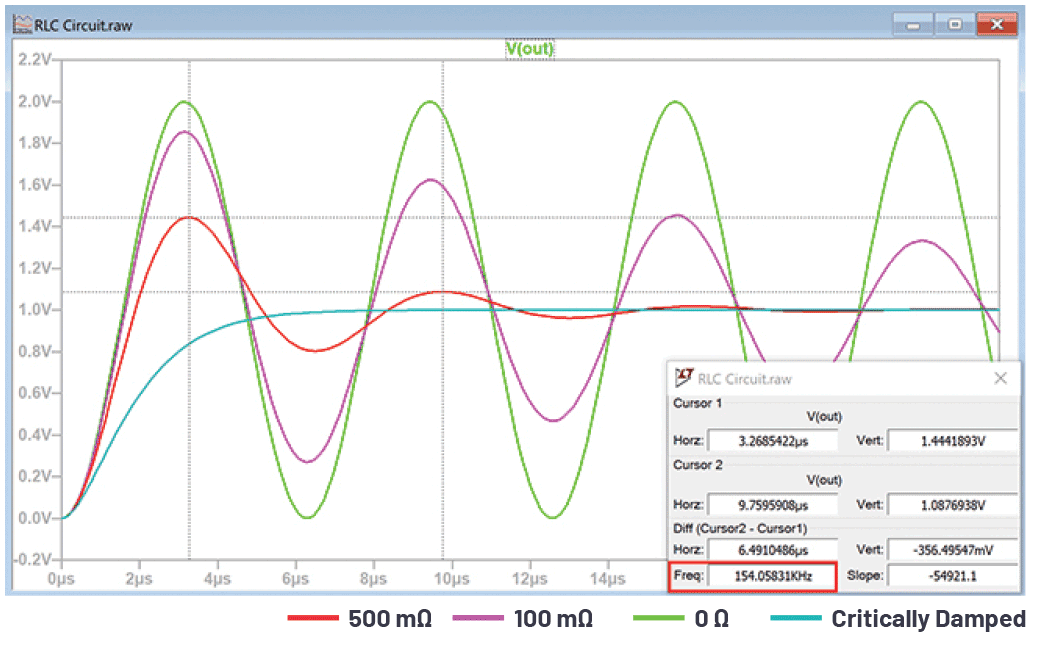
正弦波的振幅按e–ζωnt衰减。阻尼系数为0.25,固有频率ωn为1 Mrads–1,阻尼固有频率为968246 rads–1,那么方程11变成:
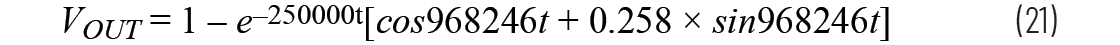
使用这个公式,计算得出VOUT在3.26 μs时为1.44 V,在9.75 μs时为1.09 V,与图4中显示的读数完全一致。
图4清楚显示了增加阻尼系数会产生的影响,即振幅和阻尼固有频率都减小。
如果我们继续增大阻尼系数,会出现什么结果?
我们知道阻尼固有频率是通过以下方程计算得出:

当阻尼系数增大到一时,阻尼固有频率减小到零。这就是所谓的临界阻尼点,此时电路中的所有振荡终止。这一点可参见方程11。自阻尼固有频率ωd减小到0,正弦项等于0,余弦项目等于一,表达式简化为一阶系统,与通过电阻充电的电容完全一样。

这一点可以参见图4中的临界阻尼线路。
不稳定系统
由于所有电路都具有电阻,所以许多电子控制电路的极点都位于左半平面,且系统本身保持稳定。但是,由方程11可以看出,负阻尼系数会导致振幅响应呈指数增长,所以极点位于右半平面会导致系统不稳定。在电路模拟中,通过插入负电阻,可以很容易看出右半平面的影响。图5显示RLC电路,其电阻为负。
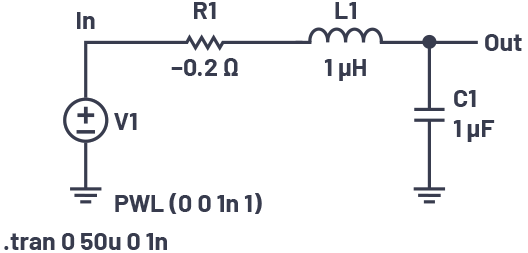
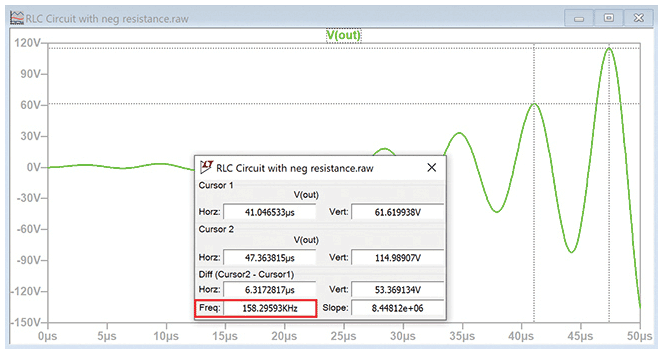
该电路的阻尼系数为-0.1。图6显示了它对阶跃输入的响应。
阻尼固有频率仍然由以下方程表示:
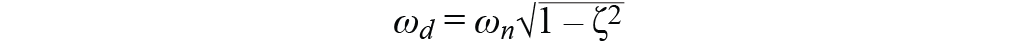
阻尼系数为-0.1时,振荡的实际频率为994987 rads–1 (158.3 kHz)。
同样,从方程11可以看出电路响应由以下公式表示:
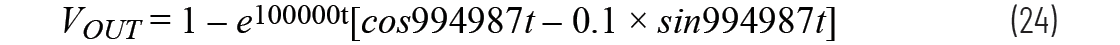
在输出增大时,我们可以得出振幅响应:VOUT在41.05 μs时,计算得出的值为61.62 V,在47.36 μs时,为114.99 V,与图6中所示的读数完全一致。
主导极点
有时一个系统由许多极点组成,使分析变得复杂。但是,如果极点之间相隔的距离足够大,那么一个极点产生的影响会占主导,因此可以忽略非主导极点,从而简化系统。
图7的上半部分显示了两个RLC电路,每个都使用完全相同的L和C元件;只是电阻发生了变化。电阻较低的电路的极点更靠近s平面的虚数轴。
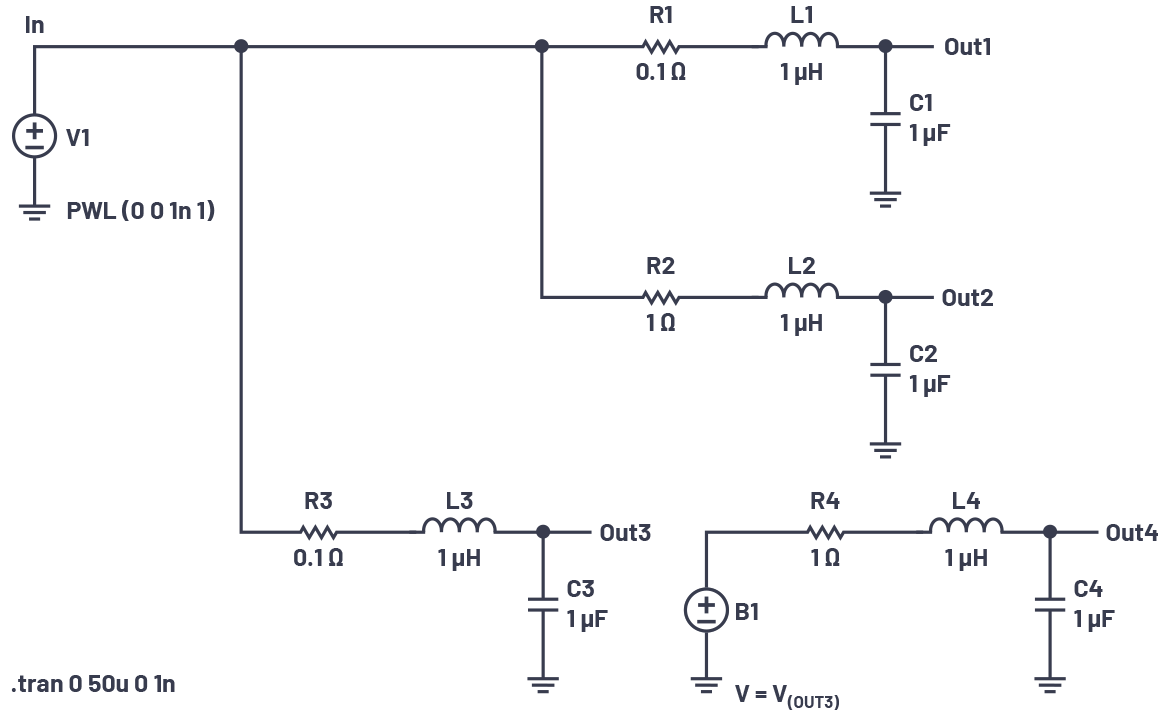
图7的下半部分显示了这两个电路的串联。我们使用行为电压源B1来复制V(OUT3),以免它被R4、L4和C4加载,以便我们查看V(OUT3) × V(OUT4)的真实响应。
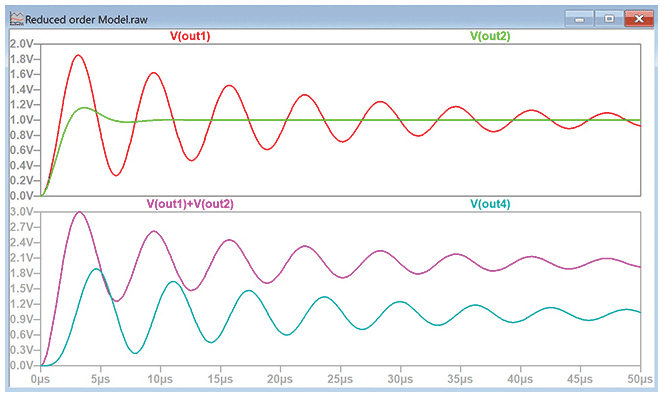
我们可以参考图8查看它们的响应。不出所料,电阻最大的电路具有最大的阻尼系数,因此其振荡衰减也最快,如图V(OUT2)所示。但是,我们注意到,当两个输出要么相加(使电路并联),要么相乘(使电路串联)时,V(OUT1)在响应中占主导。因此,要简化复杂的系统,方法之一是重点关注极点更靠近jω轴的电路,该电路会主导整个系统的响应。
在左右半面均有极点分布的系统
我们已经考虑过极点位于左半平面或右半平面的系统。如果系统在左右半面均有极点分布,会怎么样?哪一种在稳定性方面更胜一筹?为什么?
我们再次参考方程11,可以看出指数是决定系统是否稳定的决定因素。我们可以忽略方程11的正弦部分,只看指数,以了解如果我们将左半面的极点和右半面的极点结合,会发生什么。图9通过一个简单电路来进行演示。
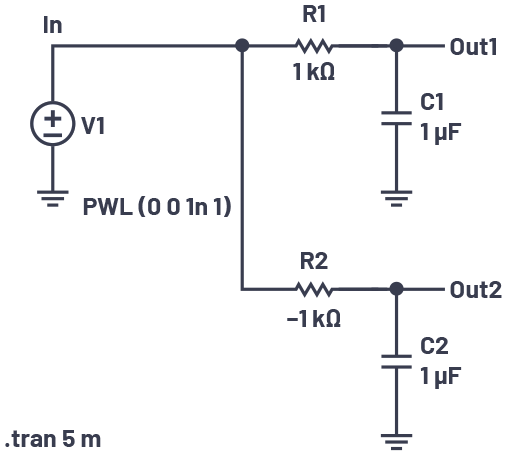
很显然,顶部的RC电路的极点位于左半面,因为它的电阻为正。底部电路的极点则位于右半面。得出此结论的数学推导如附录B所示。
图9中,电路的响应如图10所示。
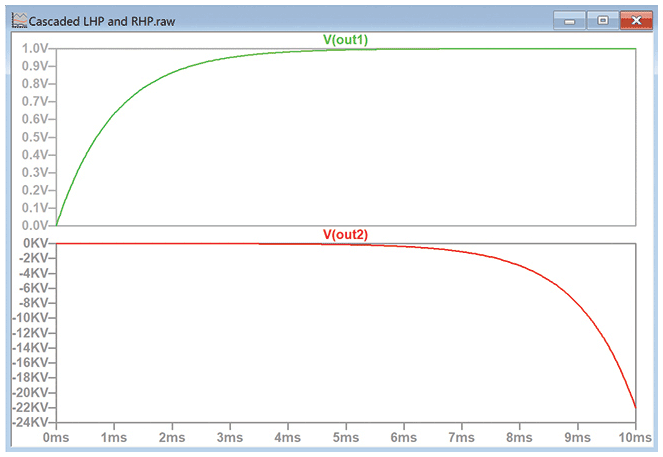
顶部波形在大约5毫秒后稳定在零梯度,这符合大众接受的规则,即RC电路将稳定在大约5个时间常数。相反,V(OUT2)的梯度不断增加。现在可以明显看出,如果将极点位于左半面的电路和极点位于右半面的电路串联,那么整个电路会不稳定,这是因为在左半面电路稳定很长时间后,右半面电路的响应会继续呈指数上升。因此,为了让电路稳定,所有极点都必须位于左半面。
结论
本文将电子控制理论中使用的理论模型与电子工程师所处的现实联系起来。受系统中的电阻(或阻尼)影响,只有当所有极点都位于左半面时,控制系统才会保持稳定。对于极点位于右半面的系统,通过测量其输出响应,结果证实存在问题,因为这需要构建负电阻模型。幸好,计算机模拟帮我们解决了这个问题,让我们能够通过简单变更电阻的极性来展示稳定和不稳定的电路。
同样,拉普拉斯变换也很少在课堂之外出现,但在验证二阶电子系统如何工作时,它们的作用可谓是无价的。
附录A
显示
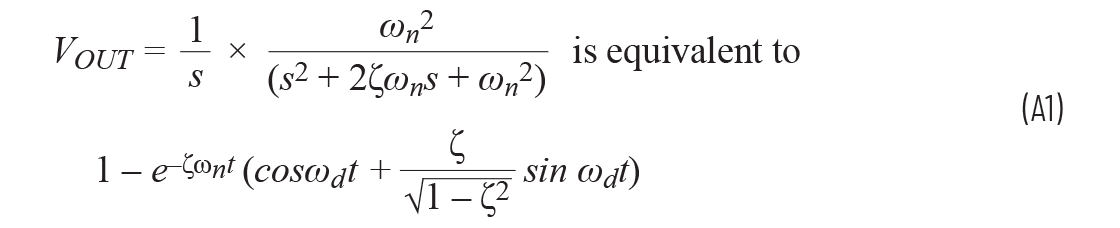
单位阶跃输入的拉普拉斯变换为

二阶低通滤波器的通用转换函数为

所以,由单位阶跃模拟的二阶系统的响应为

使用了标准的部份分式分解法,方程如下:
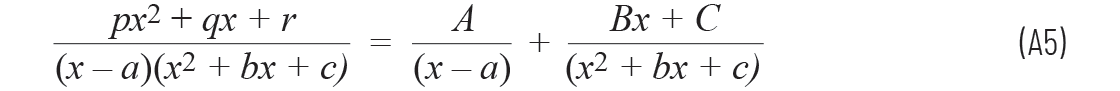
用s代替x之后,
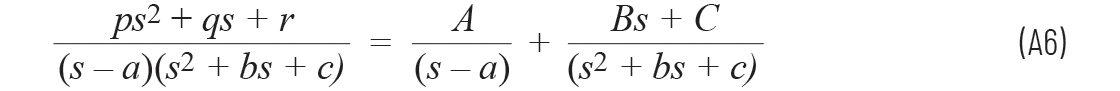
在A4中,分子中不含s或s2。而且,分母中也不含a。
所以方程A6可以改写为
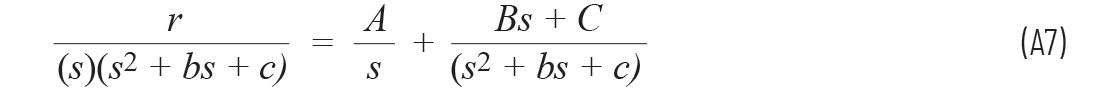
因此
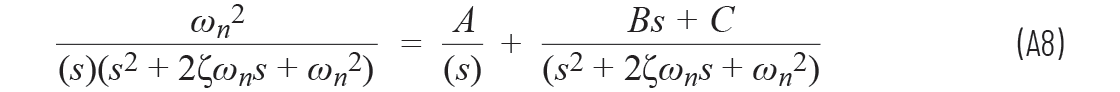
为保证方程A8两边的分母相同,可以将其改写为
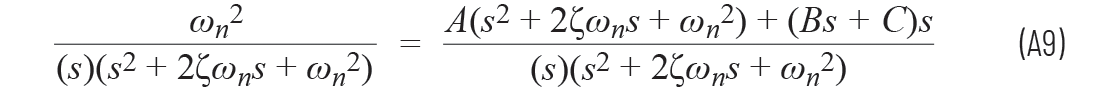
为了验证,可以将方程A9的右侧与方程A8的右侧进行比较:
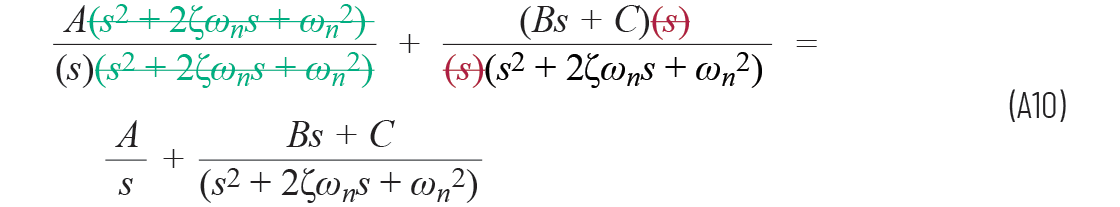
现在,我们可以使方程A9的分母相等,以求解A、B和C:
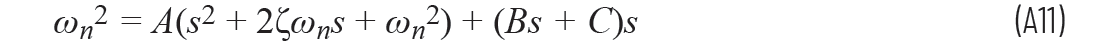
s2的系数相等:
0 = A + B
s1的系数相等:
0 = A(2ζωn) + C
s0的系数相等:
ωn 2 = Aωn 2
所以A = 1, B = –1, C = –2ζωn
因此,通过方程A8可以得出
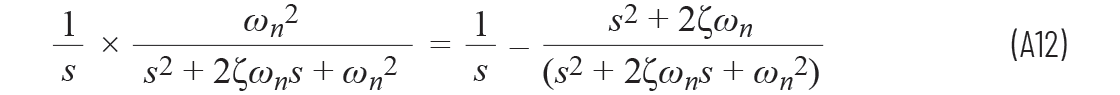
(注意符号的变化,因为B和C都为负)
从时域(左边)到拉普拉斯域(右边)有三次变换:

通过完成平方计算,我们可以把方程A12写为
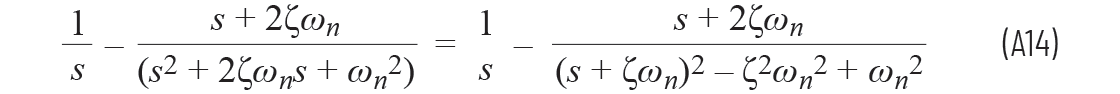
等于
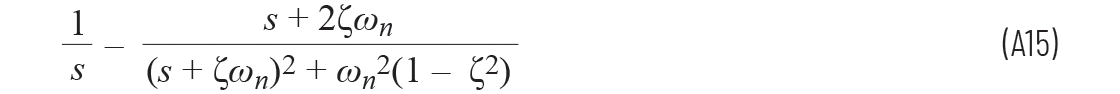
我们现在需要让分子等于 (s + 2ζωn) ,使其与分母中的第一项匹配,以便我们使用拉普拉斯定义:

因此,通过将ζωn分子项分解为分式,方程A16等于
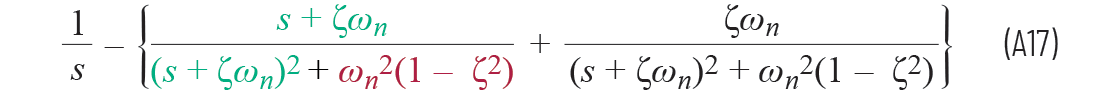
(所以, a = –ζωn b = ωn√(1 – ζ2))
我们现在需要让方程A17的第三个项等于ωn√(1 – ζ2) ,使其和分母匹配,以便我们使用拉普拉斯定义:

用方程A18的第三个项除以 ωn√(1 – ζ2),然后将 ωn√(1 – ζ2)放在分子位置。
那么整个方程可以改写为
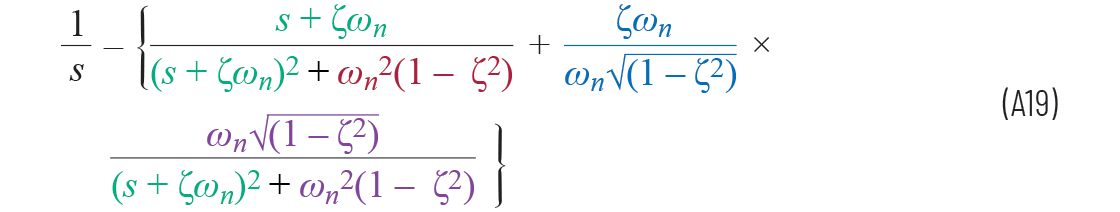
所以 a = –ζωn b = ωn√(1 – ζ2)
方程A19现在可以从拉普拉斯域中转变为
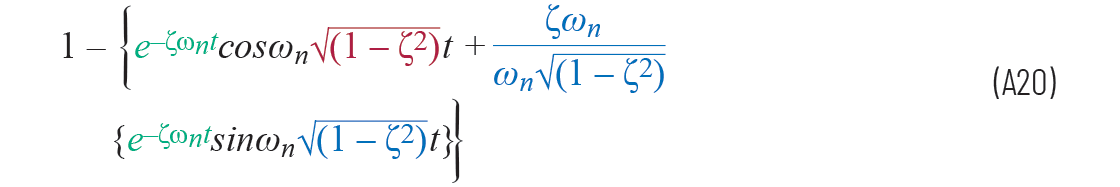
第三项中取消了两个wn。因为阻尼固有频率ωd可以写为

方程A20可以简化为
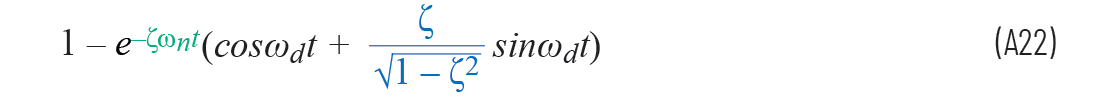
许多课本中提到,方程A21的多项式也可以写为
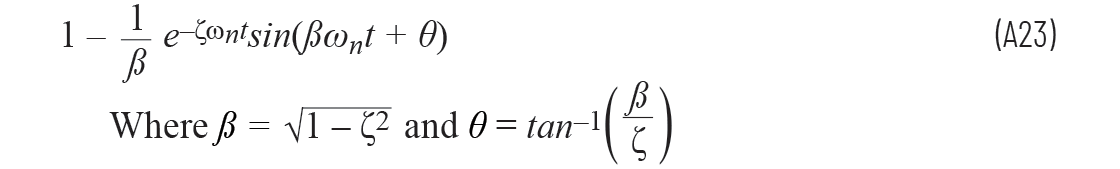
所以我们的衰减指数由阻尼系数和无阻尼固有频率决定,振荡由阻尼固有频率决定。
可以将方程A23输入电子表格和表示输出与阶跃输入之间关系的图表中。
附录B
显示
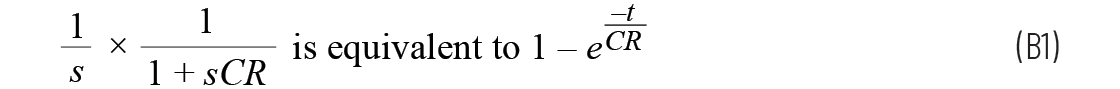
单位阶跃输入的拉普拉斯变换为

RC电路的通用转换函数为:

s为负值时,分母为零,所以这个电路的极点位于左半面上,因此系统是稳定的。如果电阻为负,那么极点位于右半面,系统会不稳定。
从方程B3可以看出,RC电路的转换函数与阶跃输入之间的关系为
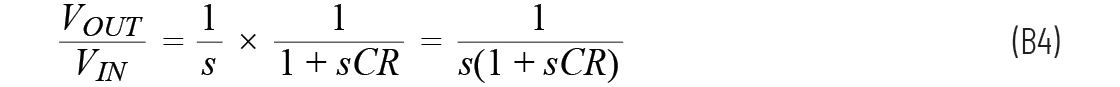
使用了标准的部份分式法,方程如下:
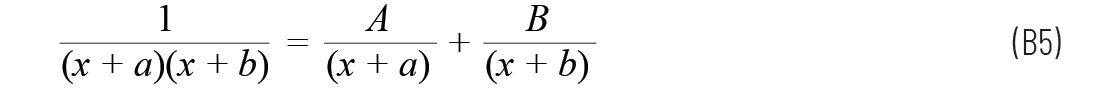
在本例中,a = 0
所以
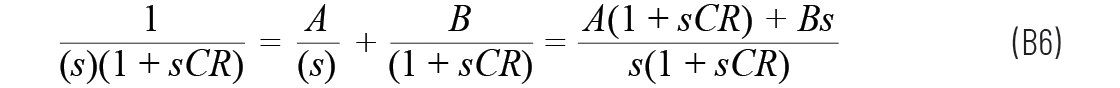
分子中s1 的相等项为
0 = ACR + B
分子中 s0的相等项为
1 = A
所以 A = 1, B = –CR
因此
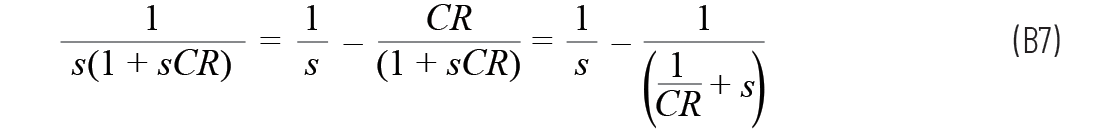
从时域(左边)到拉普拉斯域(右边)有两次变换:

将方程B7转化为采用时域意味着RC按照预期

进行响应。
附录
下载与本文相关的 LTspice® files 文件。
欲了解有关LTspice的更多信息,请访问analog.com/ltspice。
参考电路
Charles Phillips、Royce Harbor。《反馈控制系统》,第4版。Prentice Hall International,1988年。
致谢
我们采用 LTspice进行模拟。
非常感谢伦敦布鲁内尔大学的Maysam Abbod为本文实施理论校正。

