目标
本实验活动的目标是研究多相滤波器作为正交信号生成技术,并生成差分可调谐放大器,去创建一个多相放大器或者滤波器,能够生成输入信号源的四个正交相位(即以90°为增量的相位)。
背景知识
正交频率转换在现代无线收发器架构中很常见,因为当今的数字通信系统中同时部署了幅度调制和相位调制。
图1显示了简化的一阶多相电路,通常部署在许多诸如 ADL5380这样的正交解调器中。这个简单的多相电路由互补的RC子电路组 成。从输入到一个输出的低通传递函数在转折频率处使相位偏移–45°,而到另一个输出的高通传递函数在转折频率处使相位偏移+45°。两个输出之间的净相位差为90°。如果两个路径的R和C值匹配,则两条路径具有相同转折频率,更重要的是,在所有 频率下,一个输出的相位都与另一个输出保持90°的相移。两个输出信号(LO I 0°和LO Q 90°)的相对幅度仅在两个RC路径的–3 dB转折频率处相等。
正交本振(LO)信号的产生是边带抑制外差接收器中的一个重要功能模块。正交精度,即同相和正交90°相移信号的相位精度,直接决定了镜像抑制比(IRR),这是决定接收器灵敏度的重要规格参数。
材料
- ADALM2000主动学习模块
- 无焊试验板和跳线套件
- 两个1 nF电容(标记为102)
- 两个1 kΩ电阻
说明
在无焊试验板上构建图2所示的多相滤波器电路。
硬件设置
图2中的蓝色方块表示连接ADALM2000模块AWG和示波器通道的位置。试验板电路参见图3。
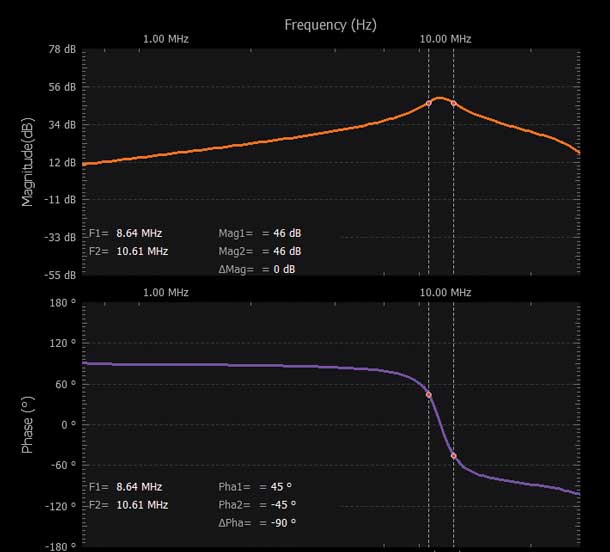
在Scopy中打开网络分析仪软件工具。配置频率扫描范围,起始频率为10 kHz,停止频率为30 MHz。将幅度设置为2 V,将偏置设置为零。选中示波器通道下拉菜单下的使用通道1作为参考 框,以测量一个输出路径相对于另一个输出路径的相位。见图4。
程序步骤
根据您使用的R和C值来计算预期的RC转折频率。运行一次频率扫描并确保将数据保存到.csv文件中,以便之后在MATLAB®或Excel中使用。
差分多相调谐放大器
通过在NPN差分放大器中添加二阶LC和CL低通和高通滤波器部分作为差分输出负载,可以生成输入正弦波信号的所有四个90°相位(0°、90°、180°和270°)。图5所示就是这种调谐放大器。
材料
- ADALM2000主动学习模块
- 无焊试验板和跳线套件
- 一对SSM2212 NPN匹配晶体管(Q1、Q2)
- 两个2N3904 NPN晶体管(Q3、Q4)
- 两个100 μH电感器(各种具有其他值的电感器)
- 两个1 nF电容(标记为102)
- 两个0.1 μF电容(标记为104)
- 两个150 Ω电阻
- 两个470 Ω电阻
- 三个1 kΩ电阻
- 一个10 kΩ电阻
- 所需的其他电阻和电容
说明
在无焊试验板上构建图5所示的电路。使用 SSM2212匹配的晶体管对作为Q1和Q2。晶体管Q3和Q4可以是2N3904器件。设置L1 = L2 = 100 μH,C1 = C2 = 1 nF。R1应等于R2,并使用值470 Ω。同样,R3应等于R4,并使用值150 Ω。
硬件设置
图5中的蓝色方块表示连接ADALM2000模块AWG、示波器通道和电源的位置。确保在反复检查接线之后,再打开电源。试验板电路参见图6。
打开电源电压控制窗口,先接通再断开固定的+5 V和-5 V电源。在Scopy中打开网络分析仪软件工具。配置频率扫描范围,起始频率为100 Hz,停止频率为30 MHz。将幅度设置为1 V,将偏置设置为零。
程序步骤
根据您使用的L和C值来计算预期的LC转折频率。
接通电源。通过交流耦合电容器(图5中的C4),将示波器输入通道2交替连接到电阻器R1、R2、R3和R4末端的四个可能的输出。运行单次频率扫描并将每次扫描存储在波形快照中,以比较每个输出的相对增益和相位响应。请务必将所有频率扫描数 据导出到.csv文件,以便采用Excel或MATLAB进行深入分析。
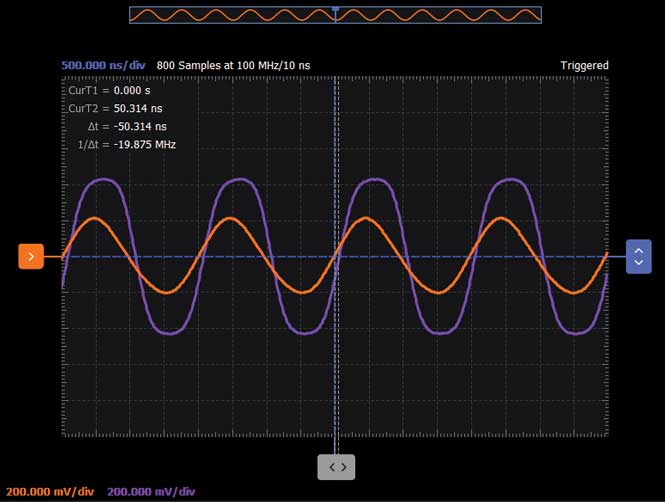
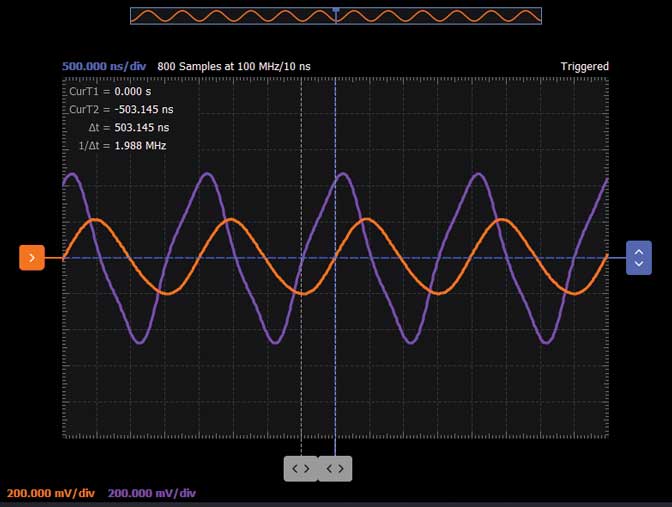
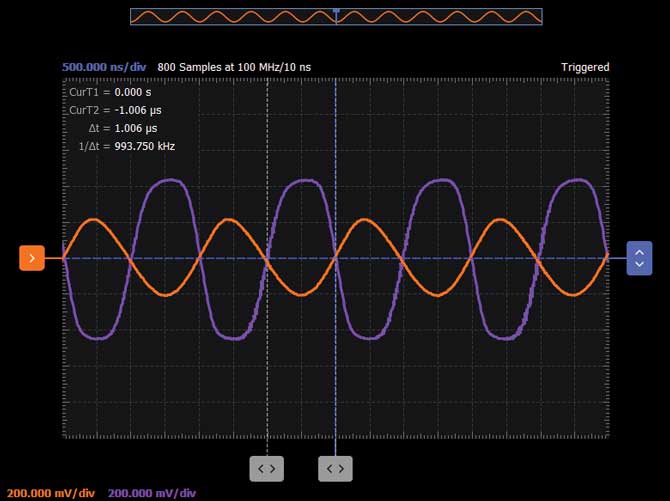
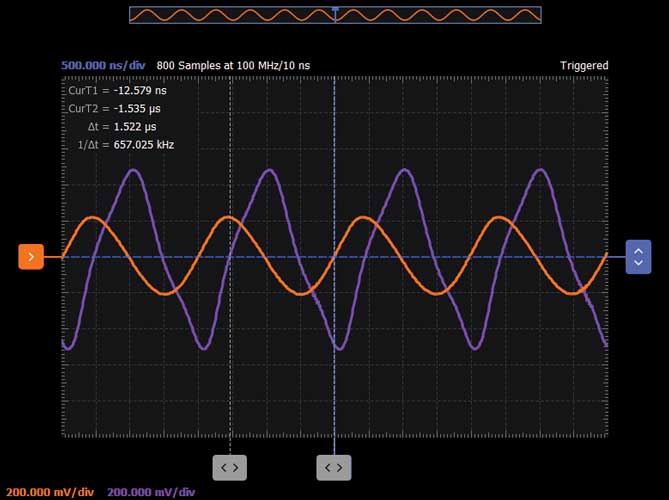
使用示波器和函数发生器软件仪器(在时域中),将AWG频率设置为谐振频率,并将幅度设置为1 V峰峰值。在示波器通道1上触发。观察四个输出的相对幅度和相位,并将每个波形存储在通道2上作为参考通道,以比较每个输出的幅度和相位。参见图7至10。
问题
能简单描述一下多相滤波器的一些实际应用吗?
您可以在 学子专区论坛上找到问题答案。