Background
Transformers are used for isolation and to convert signals from single-ended to differential. A factor often overlooked when using transformers in the front-end circuitry of high-speed A/D converters is that they are never ideal. With sinusoidal input signals, any imbalance introduced by the transformer delivers an imperfect sinusoidal wave to the input of the ADC, and results in overall data-conversion performance worse than the ADC could otherwise provide. We consider here the effects of input imbalances on ADC performance and provide examples of circuitry to achieve improved results.
About Transformers
The wide variety of available models from many manufacturers can make transformer selection a confusing process. The challenge is compounded by the differing approaches taken by suppliers in specifying performance; they often differ in the choice and definitions of the parameters they specify.
Some key parameters to consider when selecting a transformer to drive a particular ADC are insertion loss, return loss, magnitude imbalance, and phase imbalance. Insertion loss is a guide to the bandwidth capability of the transformer. Return loss, also useful, allows the user to design the termination to match the transformer’s response at a particular frequency or band of frequencies—especially important when using transformers with greater than unity turns ratios. We will focus here on magnitude- and phase imbalance, and how they affect the ADC’s performance in high-bandwidth applications.
Theoretical Analysis
Even with a wide bandwidth rating, the coupling between the transformer’s single-ended primary and differential secondary, though linear, introduces magnitude- and phase imbalances. When applied to a converter (or other differential-input device), these imbalances worsen even-order distortion of the converted (or processed) signal. While usually negligible at low frequencies, this added distortion in high-speed converters becomes significant at roughly 100 MHz. Let us first examine how the magnitude- and phase imbalance of a differential-input signal, particularly the second-harmonic distortion, affect the performance of an ADC.

Consider the input, x(t), to the transformer. It is converted into a pair of signals, x1(t) and x2(t). If x(t) is sinusoidal, the differential output signals, x1(t) and x2(t), are of the form
 |
(1) |
The ADC is modeled as a symmetrical third-order transfer function:
 |
(2) |
Then
 |
(3) |
Ideal Case—No Imbalance
When x1(t) and x2(t) are perfectly balanced, they have the same magnitude (k1 = k2 = k) and are exactly 180° out of phase (φ = 0°). Since
 |
(4) |
 |
(5) |
Applying the trigonometric identity for powers and gathering terms of like frequency,
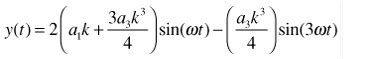 |
(6) |
This is the familiar result for a differential circuit: even harmonics cancel for ideal signals, while odd harmonics do not.
Magnitude Imbalance
Now suppose the two input signals have a magnitude imbalance, but no phase imbalance. In this case, k1 ≠ k2, and φ = 0.
 |
(7) |
Substituting Equation 7 in Equation 3 and again applying the trigonometric power identities,
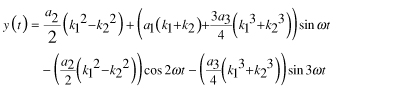 |
(8) |
We see from Equation 8 that the second harmonic in this case is proportional to the difference of the squares of the magnitude terms, k1 and k2, viz.,
 |
(9) |
Phase Imbalance
Assume now that the two input signals have a phase imbalance between them, with no magnitude imbalance.
Then, k1 = k2, and φ ≠ 0.
 |
(10) |
Substituting Equation 10 in Equation 3 and simplifying,
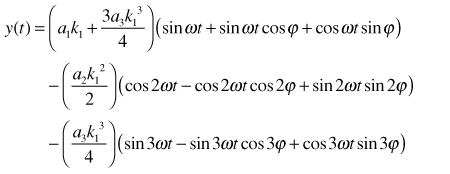 |
(11) |
From Equation 11, we see that the second-harmonic amplitude is proportional to the square of the magnitude term, k.
 |
(12) |
Observations
A comparison of Equation 9 and Equation 12 shows that the second-harmonic amplitude is more severely affected by phase imbalance than by magnitude imbalance. For phase imbalance, the second harmonic is proportional to the square of k1, while for magnitude imbalance, the second harmonic is proportional to the difference of the squares of k1 and k2. Since k1 and k2 are approximately equal, this difference is small.
As a test of the validity of these calculations, MATLAB code was written for the model described above to quantify and illustrate the impact of magnitude- and phase imbalances on harmonic distortion of a high-performance ADC with a transformer input (Appendix A). The model includes additive white Gaussian noise.
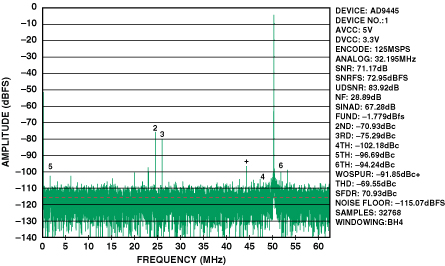
The coefficients, ai, used in the MATLAB model are for the AD9445, a high-performance 16-bit, 125-MSPS ADC. The AD9445, in the front-end configuration shown in Figure 2, was used to generate the FFT shown in Figure 3, from which the coefficients were derived.


The noise floor, second harmonic, and third harmonic here reflect the composite performance of the converter and front-end circuitry. The converter distortion coefficients (a2 and a3) and noise were computed using these measured results, combined with the 0.0607 dB of magnitude imbalance and 148 of phase imbalance at 170 MHz, specified for a standard 1:1 impedance ratio transformer.
These coefficients are used in Equation 8 and Equation 11 to compute y(t), while the magnitude- and phase imbalances are varied in the ranges 0 V to 1 V and 0 degrees to 50 degrees, respectively (the imbalance ranges of a typical transformer in the 1-MHz-to-1000-MHz range), and observe the effect on the second harmonic. The results of the simulations are shown in Figure 4 and Figure 5.


Figure 4 and Figure 5 show that (a) the third harmonic is relatively insensitive to both magnitude- and phase imbalance, and (b) that the second harmonic deteriorates more rapidly with phase imbalance than with magnitude imbalance. Thus, to achieve better performance from the ADC, a transformer configuration with improved phase imbalance is needed. Two feasible configurations, the first involving a double balun, and the second a double transformer, are shown in Figure 6 and Figure 7.
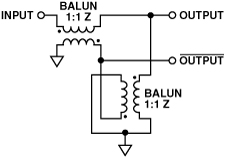

The imbalances from these configurations were compared using a vector network analyzer on specially designed characterization boards. Figure 8 and Figure 9 compare the magnitude- and phase imbalance of these configurations with that of a single transformer.


The above figures clearly show that the double configurations have better phase imbalance at the cost of slightly degraded magnitude imbalance. Therefore, using the results of the above analysis, it appears that the double-transformer configurations can be used to achieve better performance. FFT plots of AD9445 using a single transformer input (Figure 10) and a double balun input (Figure 11) show that this is indeed the case; a +10-dB improvement in SFDR is seen with a 300-MHz IF signal.

Does this mean that to achieve good performance one must couple two transformers or two baluns onto the ADC’s front end? Not necessarily. The analysis shows that it is essential to use a transformer that has very little phase imbalance. In the following examples (Figure 12 and Figure 13), two different single transformers were used to drive the AD9238 with a 170-MHz IF signal. These examples show that there is 29-dB improvement in second harmonic when the ADC is driven by a transformer that has improved phase imbalance at high frequencies.


Conclusion
The phase imbalance of a transformer can worsen the second-harmonic distortion when the transformer is used as a front end for processes (such as A/D conversion, D/A conversion, and amplification) with high-IF inputs (>100 MHz). However, by employing a pair of transformers or baluns, significant improvements can be readily achieved, at the cost of an additional transformer and extra PC board space.
Single-transformer designs can achieve adequate performance if the design bandwidth is small and a suitable transformer is chosen. However, they do require a limited matching of bandwidth, and they can be expensive or physically large.
In either case, choosing the best transformer for any given application requires detailed knowledge of the transformer’s specifications. Phase imbalance is of particular importance for high-IF inputs (>100 MHz). Even if it is not specified in the data sheet, most transformer manufacturers will provide phase-imbalance information upon request. A network analyzer can be used to measure the transformer’s imbalances as a check, or if the information is not readily available.
Appendix A
MATLAB Code Used In This Experiment:
% Matlab code to study the effect of magnitude and phase imbalance of input
% signals on the output
% Oct 19, 2005
clear all; close all;
% Error terms that can be set by the user
magnErrdB = 0; %in dB
phaseErr = 50; %in degrees
sd_noise = 100e-6; %std dev of noise
% Convert dB magnErr to voltage level
magnErr = 10^(magnErrdB/20);
% Coefficients
a0=0; %dc offset
a1=0.89; a2=0.00038; a3=0.0007; %coefficients of 1st,2nd,3rd harmonics
%to match AD9445 typical FFT
fin = 100; %input freq - does not affect calculations
t = 0:1:2047;
%Input signals
x1 = 0.5*sin((t/2048)*2*pi*fin);
x2 = 0.5*(magnErr)*sin(((t/2048)*2*pi*fin)-pi-(phaseErr*pi/180));
%Each differential signal multiplied by the transfer function
y1 = a0 + a1*x1 + a2*x1.^2 + a3*x1.^3;
y2 = a0 + a1*x2 + a2*x2.^2 + a3*x2.^3;
%Output
y = y1 - y2;
noise = sd_noise*randn(1,length(y));
y = y + noise;
% figure; plot(1000*t(1:80),x1(1:80),1000*t(1:80),x2(1:80),1000*t(1:80),y(1:80));
%Take the FFT
fft_y = fft(y/1024, 2048);
Pyy = 10*log10(fft_y.*conj(fft_y));
freq_axis = 0:1:1023;
% figure; plot(freq_axis, Pyy(1:1024), ‘-d’);
% title(‘Frequency content of the output’);
% xlabel(‘Frequency (Hz)’);
% axis tight;
%Print fundamental and 2nd, 3rd harmonics
f = Pyy(101)
h2 = Pyy(201)
h3= Pyy(301)
(Return to Text)
参考电路
- Reeder, Rob, “Transformer-Coupled Front End for Wideband A/D Converters,” Analog Dialogue, Vol. 39, No. 2, pp. 3-6, 2005.
- Mini-Circuits Data Sheet ADT1-1WT.
- Pulse Data Sheet CX2039L.
- Mini-Circuits Application Note: “How Transformers Work.”
- The Mathworks Matlab program.
- Analog Devices Data Sheet AD9445.
- Analog Devices Data Sheet AD9238.
- M/A-COM Data Sheet TP101.
- Sprague-Goodman Data Sheet GLSB4R5M102.
致谢
The authors wish to thank Ravi Kummaraguntla, Andy Morgan, and Chad Shelton for their help in the theoretical analysis and for their lab support.


