Peak Current Mode and Continuous Current Mode DC-to-DC Converter Modeling and Loop Compensation Design Considerations
Peak Current Mode and Continuous Current Mode DC-to-DC Converter Modeling and Loop Compensation Design Considerations
by
Van Yang
May 1 2016
In many applications, such as computing, the power rail’s load transient requirements are becoming more and more restrictive. Furthermore, because it involves complex Laplace transfer function calculations, the loop compensation design is often viewed as a difficult and time consuming task for many engineers.
This article discusses, step by step, the average small signal modeling of widely used peak current mode (PCM) and continuous current mode (CCM) dc-to-dc converters. With the mathematical model, ADI’s ADIsimPE/SIMPLIS, a switching circuit simulation tool is utilized to minimize the work of complex calculations. Then a simplified model is shown for simpler and faster loop compensation design and simulation. Finally, ADP2386EVAL evaluation board test results are used to prove that the loop crossover frequency, phase margin, and load transient response simulation results were well matched with the test results.
PCM Average Small Signal Modeling
As Figure 1 shows, six blocks contribute to the current mode dc-to-dc converter function: the feedback resistor divider, the compensator network, the current sensing and sampling, the comparator, the power stage, and the output network. In the loop, the inductor current ramp signal is compared with the compensator error amplifier output, which feedbacks from output voltage. The PWM signal is generated to drive the switches to modulate the inductor current. Inductor current flows into the output capacitor and load. Out of these six blocks, the power stage is the only nonlinearized block and it can be the most difficult block for dc-to-dc modeling.

Figure 1. Current-mode buck block diagram.
Modeling the power stage as a 3-terminal switch:
- Active switch mode (A)
- Common mode (C)
- Passive switch mode (P), as shown in Figure 2, we get the following Equation 1:


Figure 2. Average small signal model for the 3-terminal switch.
It’s an average model, only valid in continuous current mode, equivalent to a transformer with turns ratio 1:d. The model gets us differential Equation 2:
![]()
Small signals ![]() have been employed into the average model to become the average small signal model (ASSM). With this model, the power stage can be linearized for analysis.
have been employed into the average model to become the average small signal model (ASSM). With this model, the power stage can be linearized for analysis.
Still using the PCM CCM buck as the example, the entire regulator has been modeled into the Laplace transfer function block diagram, as shown in Figure 3. There are two control loops: the voltage loop and the current loop. In the current loop, inductor current is sensed by RT and sampled into a ramp on the first negative input of the comparator. In the voltage loop, output voltage ripple is sensed by the resistor divider with a gain of K and sampled into the compensator network Av(s) as error voltage into the comparator’s positive input. With the slope compensation ramp as the second negative input signal, the comparator generates a regulated duty cycle signal into the average small signal model of the power stage to modulate the inductor current.

Figure 3. PCM CCM dc-to-dc control model block diagram.
The gain function from inductor current to output voltage is shown in Equation 3:
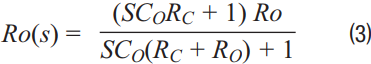
The gain function from PWM duty cycle to inductor current is shown in Equation 4:

Comparator gain Fm is shown in Equation 5, Sn is the rising slope of inductor current, Se is the slope compensation, Ts is the switch period:

The gain function of the sampling effect is shown in Equation 6:

The gain function from input voltage to inductor current is shown in Equation 7:
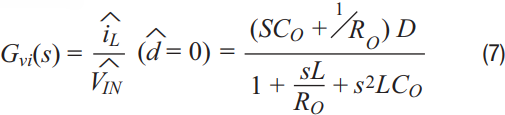
The current loop gain function is shown in Equation 8:
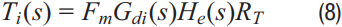
The voltage loop gain function is shown in Equation 9:
![]()
The loop gain function is shown in Equation 10:

There are four considerations for the dc-to-dc loop gain design target:
- High dc loop gain for low dc error
- Wide loop bandwidth for fast transient response
- –20 dB slope near the crossover frequency for higher phase margin (>45°)
- High attenuation at high frequency for noise attenuation
In a regulator loop, only the compensator Av(s) and the feedback resistor divider K are customized by the designer. So in the loop design, two steps are included. Firstly, disconnect the resistor divider with the output to get the open-loop gain, as shown in Equation 11:
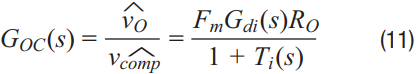
Secondly, design the compensator Av(s) to compensate the zeros and poles of the open-loop gain Goc(s) to meet the loop gain design target.
An example is shown in Figure 4 for the normal load condition when ![]() . In the low frequency domain, there are one pole (1/2πRoCo) and one zero (1/2πRcCo) and one 2-order pole (1/πfs) in the high frequency domain caused by the sampling effect He(s). Compensator Av(s) is designed to enlarge the crossover frequency, ensure a −20 dB slope near the crossover point, and to get more than a 45° phase margin. The compensator has two poles and one zero; one pole is used to compensate the open-loop gain capacitor ESR zero, the other pole functions as an integrator to increase the loop dc gain, and the zero pole compensates the open-loop load effect. The second-order pole at high frequency (1/πfs) is beneficial for noise attenuation.
. In the low frequency domain, there are one pole (1/2πRoCo) and one zero (1/2πRcCo) and one 2-order pole (1/πfs) in the high frequency domain caused by the sampling effect He(s). Compensator Av(s) is designed to enlarge the crossover frequency, ensure a −20 dB slope near the crossover point, and to get more than a 45° phase margin. The compensator has two poles and one zero; one pole is used to compensate the open-loop gain capacitor ESR zero, the other pole functions as an integrator to increase the loop dc gain, and the zero pole compensates the open-loop load effect. The second-order pole at high frequency (1/πfs) is beneficial for noise attenuation.

Figure 4. PCM CCM dc-to-dc loop design steps.
The ADsimPE tool, powered by SIMetrix/SIMPLIS, is a personal edition circuit simulator ideally suited to evaluate linear and switching components from Analog Devices. SIMetrix is very useful for linear circuits like op amps, and SIMPLIS is targeted for switching components such as dc-to-dc converters and PLLs. In Figure 5, a PCM CCM buck reference circuit has been setup as the reference to check circuit behavior and model accuracy. It’s a PCM sync buck regulator with 3.3 V input, 1.2 V output, and 1.2 MHz switching frequency.

Figure 5. PCM CCM buck SIMPLIS reference circuit.
As Figure 6 shows, in the left loop gain calculation results of the average small signal model, the crossover frequency is 50 kHz and the phase margin is 90.35°. The SIMPLIS simulation result, as seen on the right side of Figure 6, shows a 90.8° phase margin at a 47.6 kHz crossover frequency. This proves that the ADIsimPE/SIMPLIS switching circuit simulation result is matched with the complex ASSM calculation, which offers the designer a fast way for loop design. However, the schematic, as shown in Figure 5, is not very simple.

Figure 6. ASSM calculation result and SIMPLIS simulation result.
PCM Simplified Average Small Signal Modeling
Considering the crossover frequency is much bigger than 1√LCo in the application, an estimation could be performed for the complicated equations. For Equation 4, the gain function from PWM duty to inductor current, could be simplified, as shown in Equation 12:
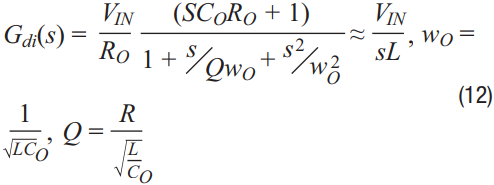
From Figure 3, we could get the open-loop gain function, which is compensator output voltage to inductor current, as shown in Equation 13:

Se is the slope of the compensation slope’s positive edge. Take

And crossover frequency is much bigger than 1√LCo, therefore, the open-loop gain function in Equation 13 could be further simplified as Equation 14:

The result is that the open-loop ASSM could be simplified, as shown in Figure 7, into a compensator output voltage controlled current source flowing into an RLC network generating inductor current. This is a much easier model to use for simulation or calculations than the original complicated equations.

Figure 7. Simplified ASSM open-loop circuit.
Using the Figure 5 reference circuit, calculate Re and Ce, then set up the closed-loop simplified ASSM circuit in ADSimPE, as shown in Figure 8. The SIMetrix simulation result is shown in the right half of Figure 8 with the crossover frequency as 49 kHz and the phase margin is 90.5°, which matches the ASSM calculation result and the SIMPLIS simulation result shown in Section 2.

Figure 8. Simplified ASSM simulation circuit and result.
ADP2386 Modeling Simulation and Test Result
The ADP2386 is a synchronous PCM CCM buck regulator from Analog Devices. It ranges from 20 V input voltage down to 0.6 V output voltage at up to 6 A output current, with switching frequency ranges from 200 kHz to 1.2 MHz. The device’s versatility allows it to be used in step-down applications and inverting buck-boost topologies without additional cost and size. In this section, the ADP2386EVAL evaluation board will be utilized to verify the model simulation results. Two tests are compared: a loop test and a load transient test.
Figure 9 shows the schematic diagram of the ADP2386EVAL. For testing, the board is set up under the conditions as shown in Table 1, row 1, below. The internal slope compensation of the ADP2386 is adaptive with duty 0.6 fs cycle, ![]() , and Equation 14 was used to get the simplified ASSM parameters as shown in Table 1, row 2. The output capacitor’s dc bias spec drops about 30% at 3.3 V, so in the simplified ASSM simulation the output capacitor value has been changed to 100 μF, not the 147 μF in the evaluation board.
, and Equation 14 was used to get the simplified ASSM parameters as shown in Table 1, row 2. The output capacitor’s dc bias spec drops about 30% at 3.3 V, so in the simplified ASSM simulation the output capacitor value has been changed to 100 μF, not the 147 μF in the evaluation board.
| VIN | VO | FS | IO | L | C | Compensator |
| 12 V | 3.3 V | 600 kHz | 3 A | 2.2 μH | 147 μF/5 Ω | 44.2 kΩ, 1.2 n, 4.7 p |
| RT | Se | Sn | Sf | Re | Ce | Gm |
| 123 mΩ | 0.2 V/μs | 0.49 V/μs | 0.18 V/μs | 2.51 Ω | 128 nF | 580 μS |
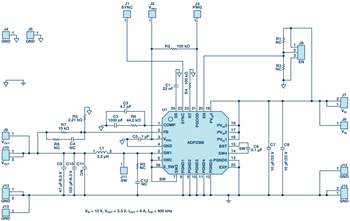
Figure 9. ADP2386EVAL schematic.
Figure 10 reveals the ADP2386EVAL loop simplified ASSM simulation and test results. The left side is the simulation by ADIsimPD/SIMetrix—the crossover frequency is 57 kHz, the phase margin is 71°. The right side is the test result under AP model 300—the crossover frequency is 68.7 kHz and the phase margin is 59.3°. Although there is a difference between test results and model simulation, we know from the ADP2386’s data sheet that its error amplifier gain is varying from 380 μS to 580 μS, coupled with the inaccuracy of the inductor and output capacitor. So this difference between the two results is acceptable.

Figure 10. ADP2386EVAL loop simulation and test results.
For the load transient test, two tests are included. Test 1 is a test under Table 1 compensator conditions with good phase margin and wide crossover frequency. Test 2 is a test with the compensator changed to 100 pF/1.2 nF/44.2 kΩ, in which the crossover frequency is down to 39 kHz and phase margin down to 36°. Figure 11 shows the load transient (0.5 A to 3 A, 0.2 A/μs) Test 1 simulation and test result. Overshoot peak is tested to be 67 mV and the simulation result is 59 mV, with the transient curves being well matched. Figure 12 shows the load transient (0.5 A to 3 A, 0.2 A/μs) Test 2 simulation and test result. The overshoot peak is tested to be 109 mV and the simulation result is 86 mV, again with the transient curves being very well matched.

Figure 11. ADP2386EVAL load transient Test 1 simulation and test results.

Figure 12. ADP2386EVAL load transient Test 2 simulation and test results.
Conclusion
Loop compensation is often viewed as a very challenging design task by engineers, especially in fast load transient applications. Based on the widely used peak current control mode continous current buck device, this article has summarized the average small signal mathmatical modeling and loop calculation, and the ADISimPE/Simplis fast and easy simulation technique. It also introduced a simplified average small signal model and offered a simplified way of handling loop compensation design. The ADP2386EVAL evaluation board loop and load transient bench test results proved the accuracy of the simplified model and its simulation.
About the Authors
Van Yang is a field applications engineer at Analog Devices in Shanghai, China. He joined ADI in 2015 to support regional medical and industrial customers in China. Prior to joining ADI, Van worked at TI as an FAE for four...




















