×

Figure 1

   

はじめに

今回はだいぶ違う切り口で、「Excel 使い」に挑戦（？）してみたいと思います。目的は、製造現場で製品（機器）ごとのばらつき誤差を得てから、高次数補正関数（誤差補正多項式）を計算し、その係数を当該製品（機器）に書き込むことで、その製品の動作を補正する（精度を向上させる）というものです。

この技術ノートでは「Excel 使ってどうやって誤差補正多項式を算出するか」という「やり方」をご紹介します。数学チックな理論ネタではございません…。以降では簡潔さを考えて「誤差多項式」という用語で説明します。

 

Excel ウィザードには敵いません…

文系の方に多いのではないかと思いますが、Excel を使い倒して、鬼のようにビジネスに使っている「ウィザード」な方がいます。私も Excelはたまに使いますが、使い方自体は、そのような方の多くが業務執行しているだろう集計や分析などの使用方法ではなく、単純な表計算だったり、ちょっとした複素数計算やグラフ描画だったりします（このグラフ描画が結構思ったようにできないのですが…）。

以前、本社（US）に「こんなリストがほしい」とメールしたら、すぐに Excel によるリストが送られてきました。これが…、「Pivot Table」が用いられていて、それを解除するのにさえ、ひと手間かかった覚えがあります。

そうでなくても「集計解析の定番であるピボット・テーブルを使えるようにならねば！」と図 1 のような書籍を購入し、数時間読んで「フムフム、簡単に使えるんだな！分かったぞ」とはなったものの、1 年以上経ったただいまでは、すっかり忘却の彼方となってしまいました。この書籍は私のデスクの横に、平積み技術書のはざまに鎮座しているままです。「アセンブラでも高級言語でも HDL でも書けるから（Python なんかはやったことないけれど）、Excel だってやる気でやればオレだってできるぜ！」とは思いつつも、実際には難儀している自らに深く絶望するものでありました（笑）。ということで、ささっと素晴らしい集計や分析、資料作成される「Excel ウィザードの方」には敵いません…。それ以前に Excel自体の機能の豊富さは、驚愕の一言です。

 

出荷前に多点補正で製品を校正したい

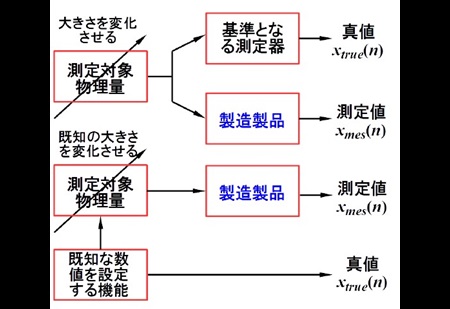
今回の技術ノートは、製造現場で以下のような補正値を算出する場合での Excelの活用法です。それ以外にもラボでのテスト・データの集計やまとめなどにも使えるものです。

1. 製造した製品の精度を高めるため誤差の多点補正をしたい
2. まず異なる数点での測定値𝑥_𝑚𝑒𝑠と真値𝑥_{𝑡𝑟𝑢𝑒}を得る
3. 測定値と真値との誤差𝑒 = 𝑥_{𝑡𝑟𝑢𝑒} − 𝑥_𝑚𝑒𝑠を各ポイントで得て、誤差多項式𝑒(𝑥)（カーブ・フィットの式）を計算する
4. 誤差多項式の係数を製品に書き込み、製品稼働時は測定値𝑥から誤差多項式𝑒(𝑥)で
   
   と補正し真値に近い測定値𝑥̂を得る

このようなケースで、「さて、どうやって誤差多項式の係数を計算（カーブ・フィット）させるか」というところで詰まってしまうのではないでしょうか。直線で補間するなら簡単ですが、2 次式や 3 次式で補正したい場合は、カーブ・フィットによる誤差多項式の係数算出はだいぶ難しそうだなと思うのではないでしょうか。ここに Excel を活用できるのです。

この技術ノートでは、まず Excelのグラフ上で単純に誤差多項式を得る方法を示し、つづいて製造用治具パソコン上で動作するVBA などで測定値と真値を Excel のセルに書き込み、カーブ・フィットにより誤差多項式の係数値をセル上で得て、それをVBA などで当該パソコンから製造中製品に書き戻しする方法を示します。

 

最初にまず分析ツールをインストールしておく

以降でやり方を示す Excelのエディションは、私が会社で使っている Microsoft Office 365 ProPlus と、自宅で使っている MicrosoftOffice Home and Business 2010 の 2 エディションです。Excel もエディションが違うとメニューの辿り方が異なりますので、折角なので 2 種類でご紹介することにしました。

 

Office 365 ProPlus では

誤差多項式の計算を Excelでするには、まず分析ツールというものをインストールしておく必要があります。Office 365 ではファイル・タブから、

ファイル ≫ オプション（左下）≫ 現れる図 2 の「Excel のオプション」の左のタブのうち、左下のアドインをクリック

そうすると図2の画面表示になります。ここで一番下の（枠で囲んだ）部分の「管理(A)」が Excel アドインになっていることを確認して、その右にある「設定(G)」ボタンをクリックします。そうすると有効なアドインを設定する、図 3 の画面になりますので、すくなくとも「ソルバーアドイン」と「分析ツール」のチェック・ボックスをチェックします。「分析ツール－VBA」も必要に応じてチェックをいれておくとよいでしょう。

 

Office Home and Business 2010 では

「2010？おぬし、なんだか古いの使ってるなぁ」と思う方も多いかと思います…。貧乏性なので、個人の PCでは古いエディションを延々と使い続けています。たしかに 2020年からすれば 10年前のエディションなわけですね！なお、このネタは[1]も参照されてください（汗）…。

ということで Office Home and Business 2010 で分析ツールをインストールするには、以下の手順で行います…、と言いたいところですが、ウィンドウのデザインは若干異なりますが、OfficeHome and Business 2010 でも同じ手順で分析ツールをインストールできます。

 

まずは単純に誤差多項式をグラフ上で表示させる方法

ここでは、セル上に誤差多項式の係数値を得る方法ではなく、簡便にその係数値のみをエクセルのグラフ上で表示させる方法をまずご紹介します。製造現場でなく、自分の実験や研究だけのために使うのであれば、このやりかたで十分でしょう。

はじめに図 4 のように測定値𝑥_𝑚𝑒𝑠(𝑛)と真値𝑥_{𝑡𝑟𝑢𝑒}(𝑛)のデータ𝑛個を得ます。これを Excel のセルに図 5 のように書き込みます。真値・測定値の順でセルに書き込むとグラフ作成の処理が簡単になります。一つ右のセル（ここでは D列）で誤差𝑒を計算させます。図 5 においてはセル D3 のみの計算式を赤枠中に示していますが、実際は全ての行で誤差𝑒の計算式を設定します。

なおこれは一般的な方法なので、手順・結果は Office 365ProPlus のみで示しておきます。

 

散布図としてグラフを描く（365 ProPlus）

つづいて測定値𝑥_𝑚𝑒𝑠と誤差𝑒のグラフを描きます。横軸である測定値𝑥_𝑚𝑒𝑠もバラつく数値（測定値）なので散布図とする必要があります。最初に、図 5 の C 列と D 列のセル全てを選択します。

つづいて Office 365 ProPlus では、挿入 ≫ グラフ・コマンド（図6）で、赤枠で囲んだ右下の斜め矢印（すべてのグラフを表示）をクリックします。そうすると図 7 の「グラフの挿入」が現れますので、右側の「すべてのグラフ」タブ（①）をクリックします。つづいて左のタブから「散布図」（②）をクリック、右上の③をクリックすると「散布図（平滑線とマーカー）」に表示が変わります。うち右上のグラフ（④）が本来の散布図ですので、これをクリック。そして OK をクリックします。そうすると図 8 のような散布図が表示されます。

 

近似曲線と誤差多項式を表示させる（365 ProPlus）

つづいて、 描いた図 8 の散布図グラフをクリックすると、図 9のように、その右側に＋マークが出てきますので、これをクリックすると同図赤枠のような「グラフ要素」が表示されます。

そのサブメニューの中の「近似曲線」のところまでマウス・カーソルをもっていきます。するとその右に三角マークが現れますから、そのうち「その他のオプション」をクリックします（図 10）。そうすると右側ペイン（枠／画面）に「近似曲線の書式設定（近似曲線のオプション）」が現れます（図 11）。

この設定メニューで「多項式近似(P)」のラジオ・ボタンを選択し、その右にある「次数(D)」で目的とする次数（3 次式なら 3）を設定します。なおこの GUI は「スピンボタン／スピンボックス」というのですね[2]！初めて知りました！

なお、どうでもいい話しですが、「多項式近似(P)」の P は「多項式」の Polynomial の P から来ているはずです。そしてその下の「グラフに数式を表示する」のチェック・ボックスにチェックを入れると、図 12 のようにグラフ上に近似曲線のカーブと多項式が表示されます。ここでは

𝑒(𝑥)=𝑎₃𝑥³+𝑎₂𝑥²+𝑎₁𝑥+𝑎₀

として、3 次の多項式としてみました。

 

Office Home and Business 2010 では

おなじ操作を Office Home and Business 2010 でやってみましょう。インストール手順と異なり、誤差多項式を表示させる方法はOffice 365 ProPlus とはだいぶ異なります。

Office Home and Business 2010 では、目的のセル全体を選択後、挿入 ≫ グラフ・コマンド（図 6 と同様）の右下の斜め矢印をクリックします。そうすると図 13 の「グラフの挿入」の画面が現れます。つづいて左のタブから「散布図」クリック、そして選択肢「散布図」のうちの左から 2 番目の「平滑線とマーカー」に相当するものをクリック。そして OK をクリックします。すると図 8 と同様な散布図が表示されます。

つづいて散布図グラフをクリックすると、リボンの上に「グラフツール」と表示されます（図 14 の上部緑色の部分）。ここでレイアウト・タブをクリックし、近似曲線をクリックします。現れたプルダウンから、さらに「その他の近似曲線オプション(M)」をクリック。こうすると図 15 の「近似曲線の書式設定」が表示されます。

以降は Office 365 ProPlus と同じように、「多項式近似(P)」のラジオ・ボタンを選択し、その右にある「次数(D)」で目的とする次数（3 次式なら 3）を設定します。さらにその下にある「グラフに数式を表示する(E)」のチェック・ボックスにチェックを入れ、「閉じる」をクリックすれば誤差多項式を表示することができます。

 

誤差多項式の係数をセル上で得る方法

しかしここまでの方法では、グラフ上に誤差多項式の各次数項の係数が数式として表示されるのみで、生産工程で VBA などを使って、各次数項の係数計算結果を製造製品（機器）に送り返す（生産物に補正式の係数値を書き込む）手順には適応できません。

これを実現するには、LINEST と INDEX という関数を用います。ここでは図 5 に示したデータを用いて行ってみます。同図のとおり測定値𝑥_𝑚𝑒𝑠(𝑛)が C3:C13 に、誤差𝑒(𝑛)が D3:D13 にあるものとします。

任意の 4 つのセルに以下を記述します[3]。これは 3 次式の例です。

=INDEX(LINEST(D3:D13, C3:C13^{1,2,3}) ,1 ,1)

=INDEX(LINEST(D3:D13, C3:C13^{1,2,3}) ,1 ,2)

=INDEX(LINEST(D3:D13, C3:C13^{1,2,3}) ,1 ,3)

=INDEX(LINEST(D3:D13, C3:C13^{1,2,3}) ,1 ,4)

この 4 つのセルがそれぞれ、3 次, 2 次, 1 次, 定数項として、誤差多項式それぞれの係数になります。

この方法を用いることで、VBA などでセルに測定値と真値を書き込み、Excel 自身のカーブ・フィットにより誤差多項式の係数値を結果セル上で得て、それを VBA などで製造用治具パソコンから製造製品に書き戻しができるようになります。

誤差多項式が 4 次より大きい場合は{1, 2, 3}を（4 次ならば）{1,2, 3, 4}、引数の最後を 1～5 にすればよいだけです。

めでたしめでたしですが、ここで INDEX と LINEST という関数の機能を確認してみましょう。

 

INDEX 関数とは

INDEX 関数は、[4]や、ネットでサーチするとその使い方が出てくるものですが、INDEX 関数の 1 番目の引数で指定した複数セルにおいて、同関数の 2 番目と 3 番目の引数（インデックス）で指定した行および列のセルの数値を返すというものです。たとえば図 5 に示したデータにおいて、

=INDEX(B3:D13, 6,2)

とすると、左上角を 1 行 1 列として、6 行 2 列目の要素である「4.9」を返します。

以下に示す「配列数式」においては、1 番目の引数で指定した単一セル内の配列数式の要素のうち、同関数の 2 番目と 3 番目の引数（インデックス）で指定した要素の数値を返します。

 

LINEST 関数 とは

LINEST 関数で、まず一番に「？」と思うのが、数式の中で使われている『{ }』です…。これはなんでしょうか…。

 

一旦話題がそれて…「{ }」は「配列数式」

回路設計 WEB ラボ。「できればいいや」ではなく、この「{ }は一体なんだ？」と好奇心・探究心が止まりません。

これを「配列数式」と呼ぶそうです[5]。{1, 2, 3}で 1×3 行列の行ベクトル（水平方向）を、{1; 2; 3}で 3×1 行列の列ベクトル（垂直方向）を一つのセルの中で表記することができます。こんな機能が EXCEL にはあるのですね…。EXCEL 奥深し！

セルに配列数式を入れるには、数式であることを明示的に示すため、

={128, 256, 512}

={128; 256; 512}

と記述します。ホントに上の式が1×3行列（行ベクトル）になっているかは、

=INDEX({128, 256, 512}, 1, 1)の答えが128

=INDEX({128, 256, 512}, 1, 2)の答えが256

=INDEX({128, 256, 512}, 1, 3)の答えが512

と得られることから確認できます。下の式が3×1行列（列ベクトル）になっているかは、

=INDEX({128; 256; 512}, 1, 1)の答えが128

=INDEX({128; 256; 512}, 2, 1)の答えが256

=INDEX({128; 256; 512}, 3, 1)の答えが512

と得られることから確認できます。行列の要素ではないところをINDEX関数で指定すると、正しい選択でないことを示す「#REF!」が表示されることから、設定と操作が正しいことも分かります。

試しにセルひとつずつに配列数式で行ベクトルと列ベクトルを記述し、これを行列の積計算ができるのか？と実験してみましたが、うまくできないようです（MMULT関数でも試してみましたがダメでした。私の修行が足りないのでしょうか？）。さすがにこのあたりがEXCELの限界でしょうか…。

ということで{1, 2, 3}は、ベクトル[1 2 3]となる、1, 2, 3という要素をもつ行ベクトルになっていることが分かりました。そしてそれが配列数式なるものなのですね。

 

気をとりなおして、再度LINEST関数とは

LINEST関数も、[6]や、ネットでサーチするとその使い方が出てくるものですが、最小二乗法を用いて直線や曲線近似を行える（その係数を算出できる）アルゴリズムです。

=LINEST(D3:D13, C3:C13^{1,2,3})

と記述すると{1, 2, 3}で3次多項式の係数を計算してくれ、これを一つのセル内に4要素の配列数式（行ベクトル）として吐き出します。それをINDEX関数で、たとえば

=INDEX(LINEST(D3:D13, C3:C13^{1,2,3}) ,1 ,1)

とすれば3次誤差多項式の3次係数𝑎3を、またたとえば

=INDEX(LINEST(D3:D13, C3:C13^{1,2,3}) ,1 ,4)

とすれば3次誤差多項式の定数項𝑎₀の数値を得ることができるわけです。

 

まとめ

あらためてExcelの凄さを体感しました。これまでも、複素数計算がExcelに組み込まれていることを発見し喜んだり、erf (error function)：誤差関数、erfc (complementary error function)：相補誤差関数という特殊な関数がExcelの分析ツールに組み込みまれており驚愕したり…、Excelには驚かされっぱなしです。それこそExcelの底まで到達するには、再度幼少から生まれなおさなければ不可能でしょう（生まれなおしても不可能でしょうが）。

今回はこのExcelの豊富な機能の一つをご紹介できたわけですが、私も皆様も「工学や数学でのExcel」を探究してみるのも楽しいかもしれません。

 

またまた余談

さきに「{ }」として配列数式というものを示しました。英語では[7]

{ = Curly Bracket or Brace

[ = Square Bracket or Bracket

( = Round Bracket or Parenthesis（複数形はParentheses）

と表現し、日本語では[8]

｛ ＝ 波括弧

［ ＝ 角括弧

（ ＝ 丸括弧

と表現するのだそうです。日本語は他にも「〈, 《, 「, 〔, 〘, 【」とかバリエーションがありますから、[8]を是非、トリビア蘊蓄（うんちく）としてご覧ください。飲み会で自慢できるでしょう（笑）。

著者について

石井 聡

1963年千葉県生まれ。1985年第1級無線技術士合格。1986年東京農工大学電気工学科卒業、同年電子機器メーカ入社、長く電子回路設計業務に従事。1994年技術士（電気・電子部門）合格。2002年横浜国立大学大学院博士課程後期（電子情報工学専攻・社会人特別選抜）修了。博士（工学）。2009年アナログ・デバイセズ株式会社入社、現在に至る。2018年中小企業診断士登録。
デジタル回路（FPGAやASIC）からアナログ、高周波回路まで多...