AN-2534: アンチエイリアシング・フィルタを備えた高性能の12 ビット、500MSPS 広帯域レシーバ

PDFをダウンロード

回路の機能とその利点

図1 に示す回路は、超低ノイズ差動アンプ・ドライバのADA4960-1 と12 ビット、500MSPS A/D コンバータ（ADC）のAD9434 をベースとした広帯域レシーバ・フロント・エンドです。3 次バターワース・アンチエイリアシング・フィルタは、アンプとADC に必要な性能とインターフェース条件に基づいて最適化されています。フィルタ回路、トランス、および他の抵抗成分による挿入損失の合計は、わずか1.2dB です。

回路全体の帯域幅は290MHz、パス・バンドの平坦性は1dB です。140MHzのアナログ入力を用いて測定したS/N比は64.1dBFS、SFDR は70.4dBc です。

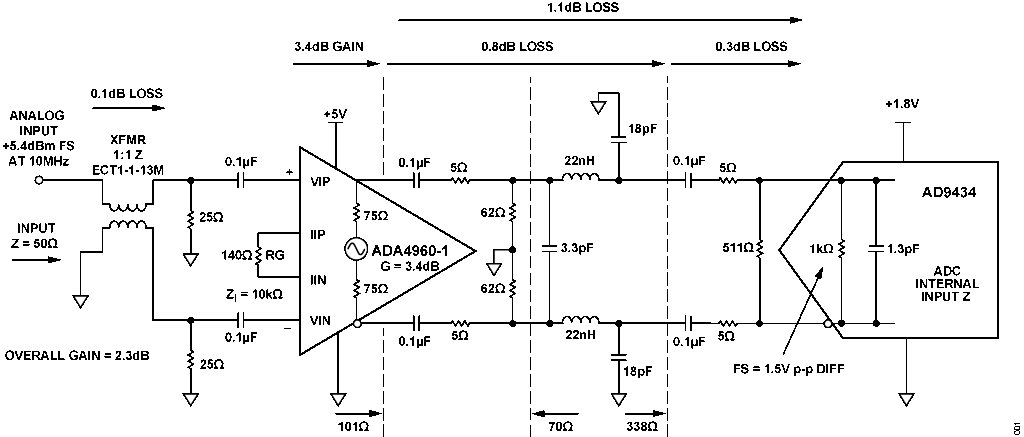
図1. 12 ビット、500MSPS 広帯域レシーバ・フロント・エンドのゲイン、損失、信号レベル（10MHz での測定値）（簡略化した回路図：全接続の一部およびデカップリングは省略されています）

図1. 12 ビット、500MSPS 広帯域レシーバ・フロント・エンドのゲイン、損失、信号レベル（10MHz での測定値）（簡略化した回路図：全接続の一部およびデカップリングは省略されています）

回路の説明

この回路は、広帯域幅（3GHz）のM/A-COM ECT1-1-13M 1:1 トランスを使用してシングルエンド入力を差動信号に変換します。5GHz のADA4960-1 差動アンプは、10kΩ の差動入力インピーダンスを持っています。外付けのゲイン設定抵抗RG を選択することでゲインを0dB～18dB の範囲で調整できます。出力インピーダンスは差動で150Ω です。

ADA4960-1 はAD9434 に最適なドライバで、ローパス・フィルタからADC 入力までを完全差動アーキテクチャにすることで、高周波数での高い同相モード除去性能を実現すると共に、2 次歪み成分を最小限に抑えます。ADA4960-1 は、外付けのゲイン抵抗に応じて0dB～18dB のゲインを提供します。この回路では、3.4dB のゲインを使用してフィルタ回路の挿入損失（1.1dB）とトランスの損失（0.1dB）を補償し、全体として2.3dB のシグナル・ゲインを実現します。約5.4dBm の入力信号から、ADC の入力でフルスケール1.5V p-p の差動信号が生成されます。

アンチエイリアシング・フィルタは3 次バターワース・フィルタで、標準的なフィルタ設計ツールを使用して設計されています。パス・バンド内で平坦な応答が得られることから、バターワース・フィルタを選択しています。3 次フィルタは1.05 のACノイズ帯域幅比を実現し、Nuhertz Technologies Filter FreeやQuite Universal Circuit Simulator（Qucs）Free Simulation などの無償のフィルタ設計ツールを使用して設計できます。

最高の性能を実現するには、正味100Ω の差動負荷をADA4960-1に加える必要があります。5Ω の直列抵抗でフィルタの容量をアンプ出力から隔離し、62Ω 抵抗が下流のインピーダンスと並列に接続されているため、10Ω の直列抵抗に接続すると正味101Ωの負荷インピーダンスになります。

ADC 入力と直列に5Ω の抵抗を接続することで、内部のスイッチング・トランジェントをフィルタとアンプから隔離します。予測可能な性能を得られるように、ADC と並列に511Ω の抵抗を接続してADC の入力インピーダンスを小さくします。

3 次バターワース・フィルタは、70Ω の信号源インピーダンス、338Ω の負荷インピーダンス、360MHz の3dB 帯域幅を使用して設計されています。設計ツールによって得られた計算値を図2に示します。

図2. 3 次差動バターワース・フィルタの設計（ZS = 70Ω、ZL = 338Ω、FC = 360MHz）

図2. 3 次差動バターワース・フィルタの設計（ZS = 70Ω、ZL = 338Ω、FC = 360MHz）

フィルタの受動部品の値には、設計ツールによって得られた値に最も近い標準値を選択しています。

2 次シャント・キャパシタの値（10.01pF）からADC の内部容量1.3pF を差し引くと8.71pF の値が得られます。この回路では、図1 に示すように2 個の18pF キャパシタをグラウンドに接続することで、この容量を実現しています。これにより同様のフィルタ処理効果が得られると共に、ある程度のAC 同相モード除去も実現できます。

このシステムの実測性能を表1 に示します。3dB 帯域幅は290MHz です。回路の総挿入損失は約1.1dB です。帯域幅応答を図3 に、S/N 比およびSFDR 性能を図4 に示します。

表1. 回路の実測性能
Performance Specs at 1.5 V p-p FS  Final Results
Cutoff Frequency (−3 dB) 290 MHz
Pass-Band Flatness (6 MHz to 200 MHz) 1 dB
SNRFS at 140 MHz 64.1 dBFS
SFDR at 140 MHz 70.4 dBc
H2/H3 at 140 MHz 85.0 dBc/70.4 dBc
Overall Gain at 10 MHz 2.3 dB
Input Drive at 10 MHz  5.4 dBm

図3. パス・バンドの平坦性性能と周波数の関係

図3. パス・バンドの平坦性性能と周波数の関係

図4. S/N 比およびSFDR 性能と周波数の関係

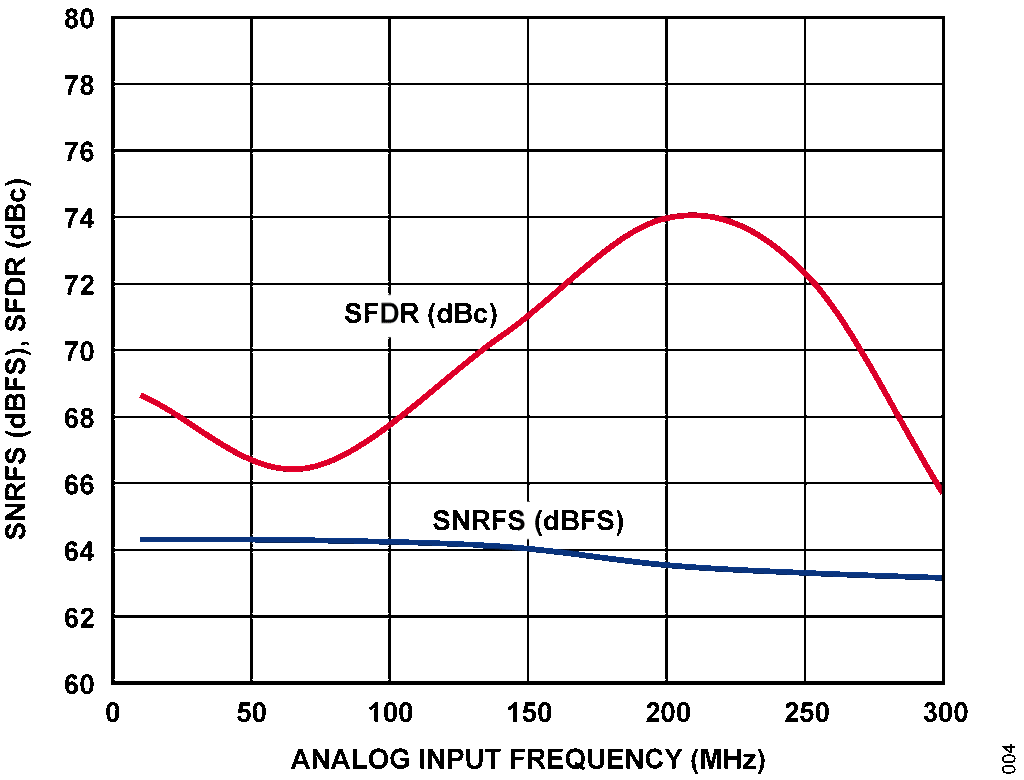
図4. S/N 比およびSFDR 性能と周波数の関係

フィルタとインターフェースの設計手順

アンプとADC による一般的な回路では、最適な性能（帯域幅、S/N 比、SFDR）を得るにはある程度の設計上の制約があります。

  1. 最適な性能を得るため、アンプに接続するDC 負荷がデータシートで推奨されている適正な値になるよう設定します。
  2. フィルタによる負荷とアンプの間には、適切な大きさの直列抵抗を接続する必要があります。これにより、パス・バンドでの不要なピーキングを防止します。
  3. 外付けの並列抵抗によってADC への入力を低減し、適切な直列抵抗を使用してADC をフィルタから隔離します。この直列抵抗は、ピーキングの低減も行います。

 

図5 に示す一般的な回路は、高速差動アンプ／ADC インターフェースのほとんどに適用でき、ここでの説明の基本として使用します。この設計手法は、ほとんどの高速ADC の入力インピーダンスが相対的に高いことと駆動源（アンプ）のインピーダンスが相対的に低いことを利用することで、フィルタの挿入損失を最小限に抑えようというものです。

図5. ローパス・フィルタを使用した一般的な差動アンプ／ADC インターフェース

図5. ローパス・フィルタを使用した一般的な差動アンプ／ADC インターフェース

基本的な設計手順は以下のとおりです。

  1. 外付けのADC 終端抵抗RTADC を、RTADC とRADC の並列接続による抵抗値が200Ω～400Ω になるように選択します。
  2. 経験値やADC のデータシートの推奨値に基づきRKB を選択します。標準的には5Ω～36Ω です。
  3. 次式を使ってフィルタの負荷インピーダンスを計算します。

     

    ZAAFL = RTADC || (RADC + 2RKB)

  4. アンプの外付け直列抵抗RAを選択します。アンプの差動出力インピーダンスが100Ω～200Ω の場合はRAを10Ω より小さくします。アンプの出力インピーダンスが12Ω 以下の場合はRAを5Ω～36Ω にします。
  5. アンプから見た合計負荷ZAL が、選択した差動アンプに適した値になるように、次式を使ってRTAMP を選択します。

    6.  

    ZAL = 2RA + (ZAAFL || 2RTAMP)

  6. フィルタの信号源抵抗を計算します。

    7.  

    ZAAFS = 2RTAMP || (ZO + 2RA)

  7. フィルタ設計ツールまたは設計テーブルを使用して、信号源インピーダンスZAAFS、負荷インピーダンスZAAFL、フィルタの種類、帯域幅、および次数からフィルタを設計します。サンプリング・レートの半分より約40%高い帯域幅を使用することで、dc～fs/2 の周波数範囲における平坦性を確保できます。
  8. ADC の内部容量CADC は、設計ツールから得られたシャント・キャパシタの最終値から差し引く必要があります。設計ツールからは、差動シャント・キャパシタのCSHUNT2 の値が得られます。最終的な同相シャント容量は、以下のようになります。

    9.  

    CAAF2 = 2(CSHUNT2 − CADC)

これらの計算を事前に行った後、以下の項目について回路を確認してください。

  1. CAAF2 は、CADC より数倍大きくなるように、10pF 以上の値にします。これにより、CADCの変化に対するフィルタの感度を最小限に抑えます。
  2. フィルタが設計テーブルや設計ツールの制限値以内に抑えるため、ZAAFS に対するZAAFL の比を7 より大きくしてはなりません。
  3. CAAF1 値を5pF 以上にして、寄生容量や部品のばらつきに対する感度を最小限に抑えます。
  4. インダクタLAAFは少なくても数nH の適切な値にします。

 

特に高次フィルタの場合などでは、フィルタ設計ツールが異なる結果を複数出力することがあります。常に、部品の値の組み合わせが適切な結果を選択してください。また、シャント・キャパシタがADC の入力容量と結合できるように、シャント・キャパシタで終端する構成を選択してください。

回路の最適化技術とトレードオフ

このインターフェース回路のパラメータは相互に大きく依存しているため、主な仕様（帯域幅、帯域幅の平坦性、S/N 比、SFDR、ゲインなど）の全てに対して回路を最適化することはほとんど不可能です。ただし、帯域幅応答においてたびたび発生するピーキングはRA とRKB を変更することで最小限に抑えることができます。

パス・バンドのピーキングは、出力の直列抵抗RA の値が増加するにしたがって小さくなります。しかし、この抵抗値が増加すると信号の減衰量が増えるので、ADC のフルスケール入力範囲を満足するためにアンプは大きな信号を駆動する必要があります。

また、RA の値はS/N 比の性能にも影響します。値を大きくすると、帯域幅のピーキングは低減しますが、同時に、ADC のフルスケールを駆動するために高い信号レベルが必要となるため、S/N 比がわずかに大きくなる傾向があります。

ADC 入力の直列抵抗RKB は、ADC の内部サンプリング・キャパシタからの残留チャージ・インジェクションによって生じる歪みを最小限に抑えるように選択します。この抵抗を大きくすることでも、帯域幅のピーキングは低減します。

しかし、RKB が増加すると信号の減衰量が増えるので、ADC の入力範囲を満足するためにアンプは大きな信号を駆動する必要があります。

パス・バンドの平坦性を最適化するもう1 つの方法として、フィルタのシャント・キャパシタCAAF2の値を少しだけ変化させるというやり方があります。

通常、ADC の入力終端抵抗RTADC は、ADC 入力の正味のインピーダンスが200Ω～400Ω になるように選択します。この値を小さくすると、ADC の入力容量の影響が小さくなるため、フィルタの設計が安定しますが、回路の挿入損失が増加します。この値を大きくしてもピーキングは低減します。

これらのトレードオフのバランスをとることは、少々困難な場合があります。この設計では、それぞれのパラメータを等しく重みづけしているため、選択した値は、全ての設計特性に対するインターフェース性能の代表値となっています。設計によっては、システム条件に応じて異なる値を選択することでSFDR、S/N 比、入力駆動レベルを最適化できる可能性があります。

この回路の信号は、アンプとその終端抵抗、およびADC 入力の間のコモンモード電圧を遮断するために0.1μF のキャパシタを使用してAC 結合されています。コモンモード電圧に関する詳細については、AD9434 のデータシートを参照してください。

受動部品とPC ボードの寄生成分に関する考慮事項

この回路に限らず高速回路の性能は、PCB レイアウトが適切であるかどうかに大きく依存します。これには電源のバイパス、制御されたインピーダンス・ライン（必要な場合）、部品の配置、信号の配線、電源プレーン、グランド・プレーンなどが含まれますが、これらに限定されません。高速ADC とアンプのPCB レイアウトに関する詳細については、チュートリアルMT-031およびチュートリアルMT-101 を参照してください。

フィルタの受動部品には、寄生成分の小さい表面実装のキャパシタ、インダクタ、抵抗を使用します。インダクタはCoilcraftの0603CS シリーズから選択しています。フィルタの表面実装キャパシタは、安定性と精度を考慮して5%、C0G の0402 タイプを使用しています。