資料ライブラリ
AN-1076: Calibrating an ADE7878-Based, 3-Phase Energy Meter
Introduction
A 3-phase energy meter built around the ADE7878 a member of the ADE78xx family of devices that has the basic structure shown in Figure 1. The phase and neutral currents are sensed using current transformers (CT), and the phase voltages are sensed using resistor dividers. A micro-controller manages the ADE78xx using I2C or SPI communications. This document explains the process of calibrating this meter. Although the configuration of this meter is 3-phase, four wires, three voltage sensors, the calibration flow does not change if other configurations are used.
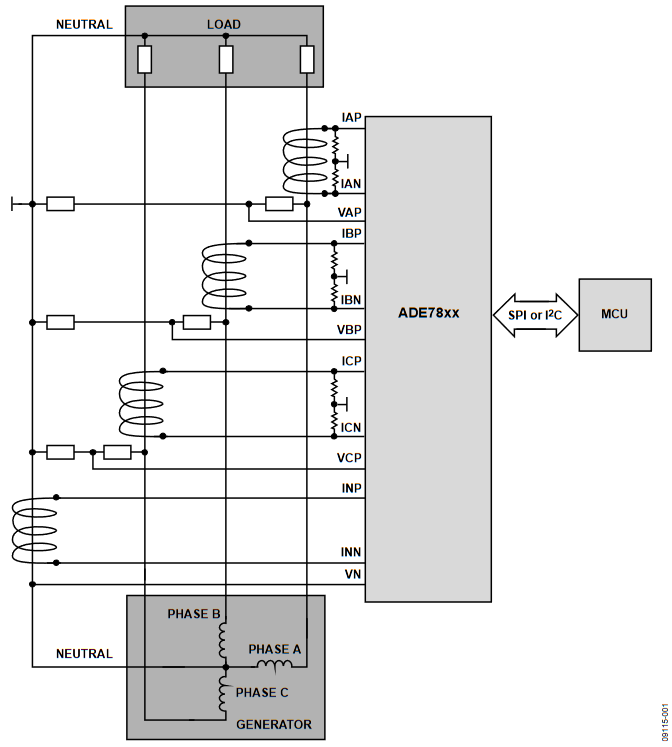
Figure 1. 3-Phase Energy Meter Structure Built Around One of the ADE78xx Family Devices.
The ADE7878, ADE7868, ADE7858, and ADE7854 are the components of the ADE78xx family. This application note refers to the ADE7878 IC, which has the largest number of features. For procedures to calibrate the ADE7868, the ADE7858, or the ADE7854, use the sections that refer to the common features of the ADE7878.
The Hexadecimal Computation section shows how a 24-bit signed representation can be obtained for a signed fractional number, and how the two 24-bit bit representations can be obtained for the WTHR, VARTHR, and VATHR 48-bit registers.
Figure 2 shows the functional block diagram of the ADE7878. The quantities that need to be calibrated are presented: xIGAIN, xVGAIN, xPHCAL, xWATTOS, xWGAIN, xVAROS, xVARGAIN, xFWATTOS, xFWGAIN, xFVAROS, xFVARGAIN, xVRMSOS, NIGAIN, and NIRMSOS (x = A, B, or C). Depending on ADE78xx IC used, some of these quantities may not be calibrated. For example, the ADE7858 does not compute the fundamental active/reactive powers; therefore, xFWATTOS, xFWGAIN, xFVAROS, and xFVARGAIN do not need to be calibrated in this case.
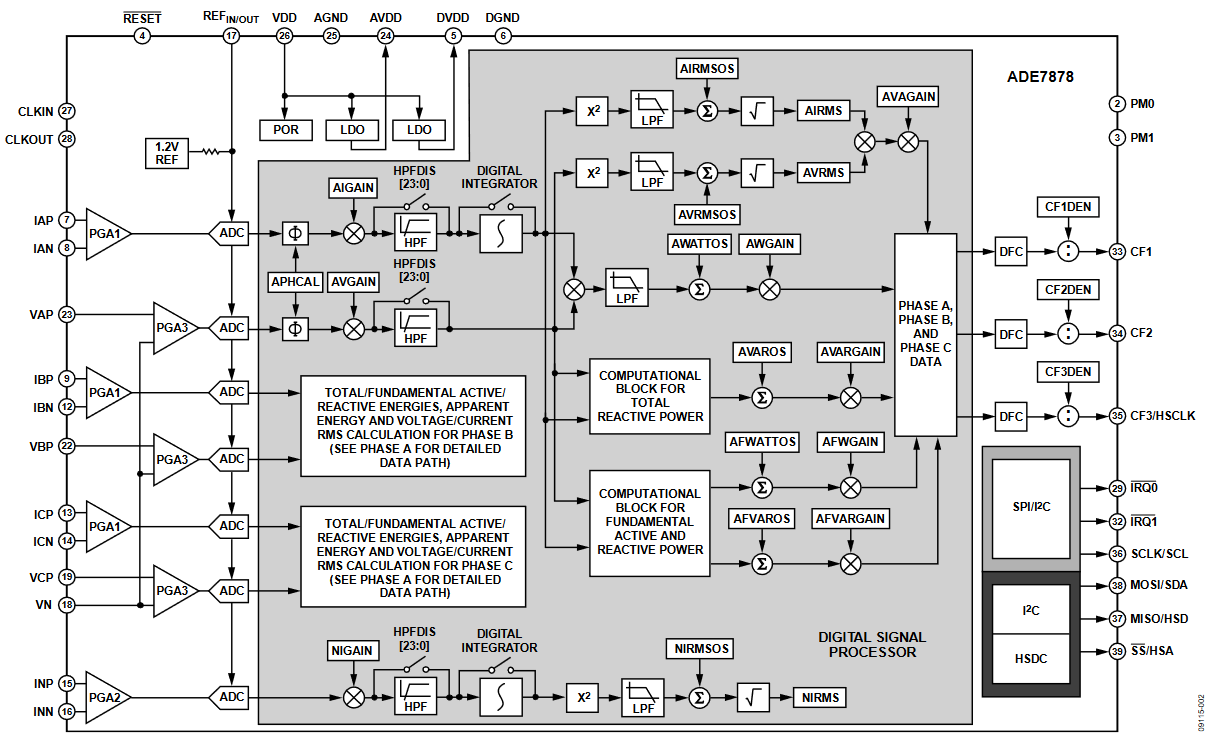
Figure 2. ADE7878 Functional Block Diagram.
The external components, together with the internal analog-to-digital converters (ADCs), introduce metering errors. The gain calibration compensates the amplitude errors determined by the current transformers, resistor dividers, and the ADCs. The phase calibration compensates the phase delay introduced by the current transformers. Offset compensation is necessary to eliminate the effect of the correlated noise present in various data paths.
Calibration Methods
Two methods are used to calibrate a 3-phase energy meter: one using a reference meter and one using an accurate source.
The reference meter method supposes the source is able to provide various currents and voltages without too much accuracy and stability. The readings of the meter in calibration are compared against the reference meter readings, and the quantities to calibrate are adjusted accordingly.
The accurate source method supposes the source can provide exact currents and voltages. The readings of the meter in calibration are compared against expected values, and the quantities to calibrate are adjusted accordingly.
Both methods require the computation of the CFxDEN (x = 1, 2, or 3) registers, full-scale current (IFS), and full-scale voltage (VFS) based on the meter specifications.
COMPUTING CFxDEN, IFS, AND VFS
An energy meter is usually characterized by the nominal current (IN), nominal voltage (VN), and the meter constant (MC). The meter constant expresses how many impulses are generated at the CF1, CF2, or CF3 pulse output pins every kWh.
CFxDEN is a positive integer used in the energy-to-frequency converter block of the ADE7878. The CF1DEN, CF2DEN, and CF3DEN registers are initialized with this value.
The expression used to calculate its value is:
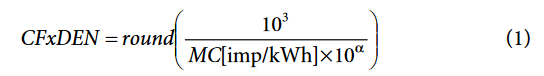
where:
MC is the meter constant expressed in impulses/kWh.
10α with α < 0 determines how much energy is assigned to 1 LSB of various energy registers, such as WATT-hour and VAR-hour.
For example, MC = 6400 imp/kWh in the energy meter to calibrate. To obtain a positive integer CxFDEN, chose α = −3.
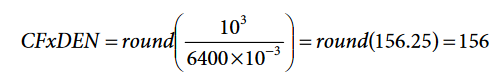
where α = −3 means that 1 LSB of the energy registers counts as 10-3 Wh, 10-3 VARh, or 10-3 VAh.
Figure 3 presents the current transformer input structure normally used on an ADE7878-based 3-phase meter. Based on the current transformer characteristics and the burden resistors (R1 and R2), compute the full-scale current (IFS), that is, the rms of the sinusoidal current that determines a full-scale sinusoid at the current channel ADC inputs as follows:
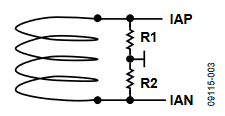
Figure 3. Phase Current Input Structure with Current Transformer.
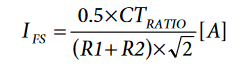
where:
R1 and R2 are the burden resistors.
CTRATIO is the current transformer input-to-output ratio, and 0.5 V is the maximum allowed voltage at the ADC inputs.
Note that, for simplicity, Figure 3 does not show the antialiasing filter that must be placed between the coil and the ADE7878. A simple RC filter with a corner frequency of f0 > 2 kHz should be used.
Figure 4 presents the Rogowski coil input structure used on an ADE7878-based 3-phase meter. Based on the voltage per amp ratio of the coil, RGCRATIO [V/A], the full-scale sinusoid at the current channel ADC inputs can be computed.
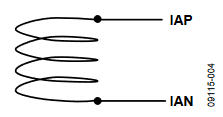
Figure 4. Phase Current Input Structure With Rogowski Coil.
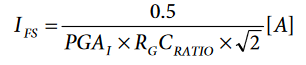
where PGAI is the PGA gain in the current channel. Note that for simplicity, no filter is shown between the coil and the ADE7878. However, with Rogowski coils, two cascaded filters should be placed one immediately after the coil, with a corner frequency of 10f0 compensates for the 20 dB/dec gain of the coil, followed by the regular antialiasing filter with a corner frequency, f0.
Figure 5 presents the resistor divider normally used to measure the phase voltage in an ADE7878-based 3-phase meter. The full-scale voltage (VFS) can be computed, that is, the rms of the sinusoidal voltage that determines a full-scale sinusoid at the voltage channel ADC inputs.
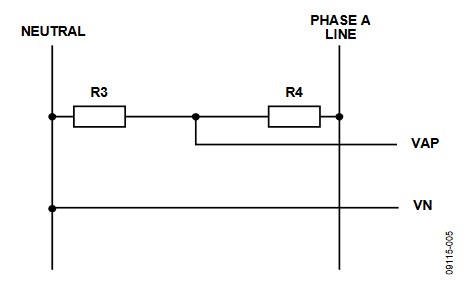
Figure 5. Phase Voltage Input Structure.
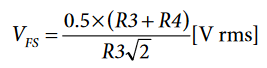
where R3 and R4 are the resistor divider components, and 0.5 V is the maximum allowed voltage at ADC inputs.
Configure the ADE7878
In general, before starting any calibration procedure, the ADE7878 is switched into PSM0 normal power mode, some registers are initialized, and the digital signal processor (DSP) is started. The following are step-by-step instructions to do this:
- Power up the ADE7878 and change it to PSM0 normal power mode by setting PM1 pin low and PM0 pin high.
- Set the PGA gain in the current and voltage channels in the gain register at the desired values.
- Enable the high-pass filter (HPF) in the data path by setting HPFDIS = 0x0.
- Clear Bit 0 (INTEN) of the CONFIG register if a regular current transformer (CT) is used. Set Bit 0 (INTEN) of the CONFIG register to 1 if a Rogowski coil is used to enable the digital integrator.
- Initialize the CF1DEN, CF2DEN, and CF3DEN registers with the CFxDEN value of 1.
- Initialize the VLEVEL register by:
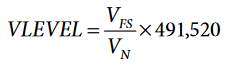
where VN is the nominal phase voltage of the meter. - Enable the CF1, CF2, and CF3 pins by setting Bit 9 (CF1DIS), Bit 10 (CF2DIS), and Bit 11 (CF3DIS) to 0 in the CFMODE register.
- Set COMPMODE = 0x3911 to enable the CF1 function of the Phase A energy, the CF2 function of the Phase B energy, and the CF3 function of the Phase C energy.
- Set the RUN register to 0x1 to start the internal DSP.
Accurate Source Method
Current and Voltage RMS Calibration
Calibration of the xIGAIN and xVGAIN Registers
Previously, it was shown how the CFxDEN registers can be calculated to accumulate energy in submultiples of watt-hour, VAR-hour, or VA-hour. Similarly, current and voltage rms gain registers allow the computation of the rms registers in submultiples ampere and volt, respectively.
For example, the meter is supplied with its nominal voltage (VN) = 220 V rms. The VGAIN registers can be calibrated for the ADE7878 to compute the rms value as V rmsREF = 220 × 104 [100 µV]. Similarly, if the meter is supplied with its nominal current (IN) = 1.5 A rms, the IGAIN registers may be calibrated for the ADE7878 to compute the rms value as I rmsREF = 1.5 × 106 µA.
The following lists the limitations that must be considered when choosing V rmsREF and I rmsREF:
- xIGAIN and xVGAIN cannot be set outside the −1 to +1 range.
- Full-scale inputs should still be represented on a 24-bit signed number format after xIGAIN and xVGAIN have been introduced.
- When the amplitude of the voltage at the input of the zero-crossing circuit is lower than 10% of full scale, no zero crossing events are triggered. Choose VGAIN to have at least the amplitude of the nominal voltage above this 10% threshold.
This approach simplifies the rms processing tasks that are executed inside the microcontroller. If this is not desired, simply choose V rmsREF and I rmsREF at values derived from 4,191,910, the ideal rms value computed by the ADE7878 when the inputs are at full scale.
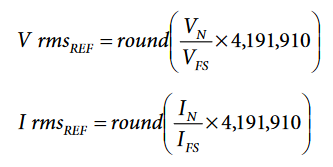
For example, in the energy meter to calibrate, if IFS = 7 A rms, VFS = 350 V rms, VN = 220 V rms, and IN = 1 A rms, then:
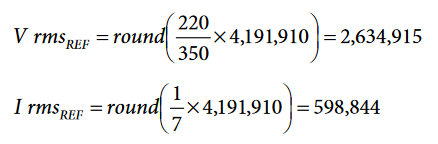
The procedure to calculate xIGAIN and xVGAIN follows:
- Supply each phase of the meter with a nominal current, nominal voltage, and a power factor of 1.
- Enable the zero crossing interrupts (ZXVA, ZXVB, ZXVC, ZXIA, ZXIB, and ZXIC) one at a time in the MASK1 register. Read the corresponding phase rms value xVRMS or xIRMS (x = A, B, or C) when the interrupt is triggered for multiple times and average them. Let this average be rms.
- Decide the desired rms representation for the nominal voltage or current. Let it be RMSREF.
The xVGAIN or xIGAIN calibrated value is the signed 24-bit hexadecimal representation of the following:
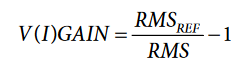
The neutral current does not have zero-crossing supervision; therefore, the NIRMS register should be read periodically with the period determined by the period register, and then its average should be used in the previous expression.
Calibration of the IRMSOS and VRMSOS Registers
The AIRMSOS, BIRMSOS, CIRMSOS, NIRMSOS, AVRMSOS, BVRMSOS, and CVRMSOS registers compensate the dc offsets produced by the noise in the phase currents and voltages. The compensation procedure is as follows:
- Supply each phase of the meter with a nominal current (IN), nominal voltage.
- Enable the zero-crossing interrupts (ZXIA, ZXIB, ZXIC, ZXVA, ZXVB, and ZXVC) one at a time in MASK1 register. Read the corresponding phase rms value xIRMS or xVRMS (x = A, B, or C) when the interrupt is triggered for multiple times and compute the average, the result of which is IRMSN or VRMSN.
- Supply each phase of the meter with the minimum current, IMIN, for which the current rms must be measured or the minimum voltage, VMIN, for which the voltage rms must be measured. Note that the zero-crossing detection circuit is disabled when the voltage signals go below 10% of full scale. If the VMIN is below this threshold, then the xVRMS registers should be read periodically with the period determined by the period register, without using the ZXVA, ZXVB, and ZXVC interrupts.
- Read the xIRMS or xVRMS registers multiple times at the zero-crossing interrupts, average the readings, and call this number IRMSMIN or VRMSMIN.
The xIRMSOS calibrated value is the signed 24-bit hexadecimal representation of the following:
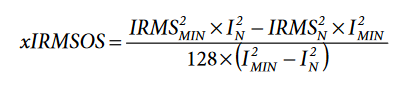
Similarly, the xVRMSOS calibrated value is the 24-bit hexadecimal representation of the following:
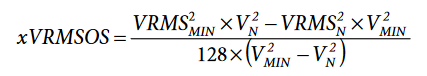
To estimate the rms offset in the neutral current, read the NIRMS register periodically with a period determined by the period register and follow the previous procedure.
Total and Fundamental Active Energy Calibration
To perform the total active energy calibration using an accurate source, execute the following operations:
- Set the WTHR, VARTHR, and VATHR registers at the value indicated in Equation 2.
- Configure the ADE7878 in line cycle accumulation mode.
- Supply the meter with accurate nominal phase voltages, nominal phase currents, and phase power factors equal to 1.
- Calibrate the AWGAIN, BWGAIN, and CWGAIN registers.
- Supply the meter with accurate nominal phase voltages, nominal phase currents, and phase power factors equal to 0.5.
- Calibrate the APHCAL, BPHCAL, and CPHCAL registers.
- Supply the meter with accurate nominal phase voltages, minimum phase currents at which the meter must be certified, and phase power factors equal to 1.
- Calibrate the AWATTOS, BWATTOS, and CWATTOS registers.
The fundamental active energy calibration is not necessary because the gains and offsets computed for the total active energy should be the same. However, for outstanding accuracy, fundamental active energy can still be calibrated using the same procedure presented in the following sections for the total active energy calibration.
Calibration of the WGAIN Registers
As already stated, the calibration of gain registers is necessary to compensate for small amplitude errors determined by the current transformers, resistor dividers, and the ADCs. This is fully accomplished by the xIGAIN and xVGAIN registers. In addition, the xWGAIN registers compensate for the time measurement error introduced by the crystal providing the CLKIN signal to the ADE7878. Usually, this error is small and can be overlooked. In this case, if the xIGAIN and xVGAIN registers have been introduced, then introduce the WTHR register based on the following formula:
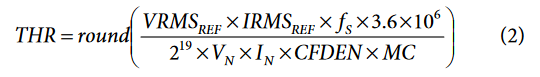
where fS = 8 kHz is the frequency with which the DSP computes the instantaneous power.
THR must always be greater or equal to PMAX, the active power computed by the ADE7878 when the phase voltage and phase current have full-scale amplitudes:
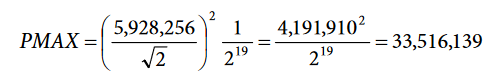
If THR is less than PMAX, adjust VRMSREF or IRMSREF.
For example, to calibrate an energy meter where IFS = 7 A rms, VFS = 350 V rms, VN = 220 V rms, and IN = 1 A rms, then the threshold is:
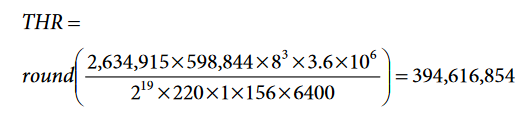
In hexadecimal, this number is THR = 0x17856016. Because WTHRx, VARTHR,x and VATHRx are 48-bit signed registers, they are initialized into the ADE7878 memory using two 24-bit registers, THR1 = 0x17 and THR0 = 0x856016.
If the time measurement error introduced by the crystal requires compensation, then the procedure to calibrate AWGAIN is as follows:
- Supply Phase A of the meter with accurate nominal current, nominal voltage, and a power factor of 1 (0° delay between the current and voltage on the same phase).
- Set the ADE7878 in line cycle accumulation mode for total active energy by setting Bit 0 (LWATT) and Bit 3 (ZXSEL[0]) to 1 in the LCYCMODE register.
- Compute the LINECYC register that determines the accumulation time. Usually, the watt-hour registers have a four-digit number at the end of the accumulation to allow a sufficient margin for gain correction. The following expression should give an indication of the minimum value:
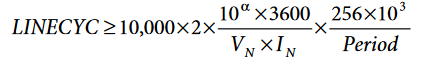
where:
Period is the content of the ADE7878 register showing the duration of a line cycle period.
VN is the nominal phase voltage of the meter.
IN is the nominal phase current of the meter. - Compute the content that the AWATTHR register would have if under ideal conditions by:
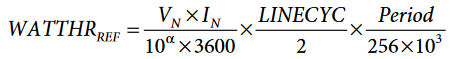
- Enable LENERGY interrupt in the MASK0 register by setting Bit 5 (LENERGY) to 1.
- Read the AWATTHR register when interrupt IRQ0 is triggered. Then cancel the interrupt flag in the STATUS0 register by writing STATUS0 when Bit 5 (LENERGY) is set to 1. Repeat this operation multiple times and use the arithmetical average of WATTHR in the following equation.
AWGAIN is the signed 24-bit hexadecimal representation of the following:
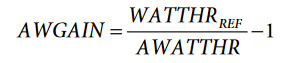
Repeat the procedure for Phase B and Phase C to determine BWGAIN and CWGAIN. Instead of setting Bit 3 (ZXSEL[0]) to 1 in the LCYCMODE register, set Bit 4 (ZXSEL[1]) and Bit5 (ZXSEL[2]) in the LCYCMODE register, respectively.
As an alternative, instead of reading the energy registers, simply set Bit 0 (TERMSEL1[0]) to 1, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register, read the CF1 pin frequency and compare it to the desired CFREF as follows:
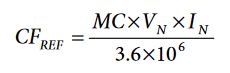
AWGAIN is then the signed 24-bit hexadecimal representation of the following:
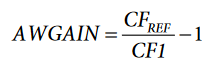
Repeat the procedure to determine BWGAIN by setting Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 1, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register. To determine CWGAIN, set Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 1 and repeat the procedure.
Calibration of the xPHCAL Registers
As was previously stated, the phase calibration is necessary to compensate for the phase delay introduced by the current transformers. The procedure to calibrate the APHCAL, BPHCAL, and CPHCAL registers is as follows:
- Supply each phase of the meter with a nominal current, nominal voltage, and power factor equal to 0.5 inductive (the current has a delay of 60° relative to the voltage on the same phase).
- Use the same initializations as in Calibration of the WGAIN Registers section for each phase.
- Compute the content that the AWATTHR register would have if under ideal conditions by:
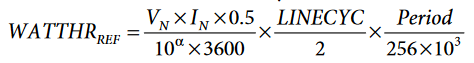
- Read the AWATTHR register when interrupt IRQ0 is triggered. Then cancel the interrupt flag in the STATUS0 register by writing STATUS0 when Bit 5 (LENERGY) is set to 1. Repeat this operation multiple times and use the arithmetical average of AWATTHR in the next equation.
- Compute the angle representing the delay error between the phase current and phase voltage by
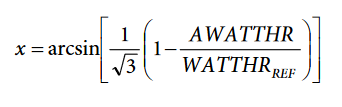
The phase resolution of the timer used to compensate the phase delay is:
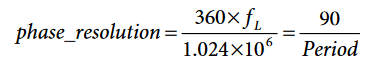
where:
FL is the line frequency of the system.
Period is the ADE7878 register indicating the line period of the phase voltage.
Divide x by the phase_resolution and compute the APHCAL number by:
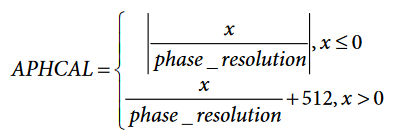
Note that the previous expressions imply x is obtained in degrees. If x is obtained in radians, then the phase resolution formula changes to:
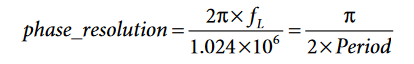
Repeat the procedure for Phase B and Phase C to determine BPHCAL and CPHCAL.
As an alternative, instead of reading the energy registers, simply set Bit 0 (TERMSEL1[0]) to 1, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register, read the CF1 pin frequency and compare it to the desired CFREF by:
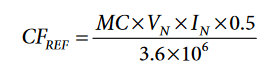
The delay error between the phase current and phase voltage is:
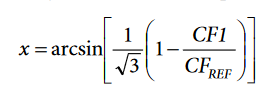
Then, the procedure to compute APHCAL is identical to the procedure previously mentioned.
Repeat the procedure to determine BPHCAL by setting Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 1, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register. To determine CPHCAL, set Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 1 and repeat the procedure.
If the phase errors in the system are large, they may introduce gain errors that are not compensated for during the WGAIN calibration. In this case, after the phase errors are compensated for, gain calibration must be executed one more time to eliminate these potential errors.
Calibration of the WATTOS Registers
As previously stated, the offset compensation is necessary to compensate for the effect of the correlated noise present in the data paths. The procedure to calibrate AWATTOS, BWATTOS, and CWATTOS is as follows:
- Supply each phase of the meter with accurate nominal current, nominal voltage, and a power factor of 1 (0° delay between the current and voltage on the same phase).
- Set LINECYC and WTHR to the values LINECYCN and WTHRN used during the WGAIN calibration.
- Read AWATTHR and name its value AWATTHRN.
- Supply each phase of the meter with the minimum current for which the desired accuracy is required, with the nominal voltage and a power factor of 1 (0° delay between the current and voltage on the same phase).
- Use the same initializations as in Calibration of the WGAIN Registers section.
- Set the WTHR register equal to WTHRMIN = PMAX to increase the frequency at the CF1 pin now that the phase current is small, which decreases the calibration time significantly.
- Compute the LINECYC register that determines the accumulation time. Usually, the watt-hour registers should have at least a two-digit number at the end of the accumulation to allow sufficient margin for gain correction. If longer accumulation times are acceptable, then a three-digit number may also be considered. The following expression should give an indication of the minimum value:
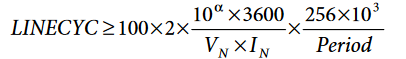
- Read AWATTHR and name its value AWATTHRMIN.
AWATTOS is then the signed 24-bit representation of the following:
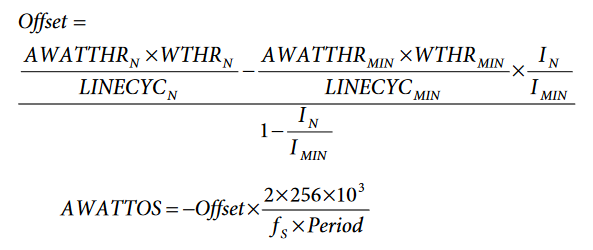
Repeat the procedure for Phase B and Phase C to determine BWATTOS and CWATTOS.
As an alternative, instead of reading the energy registers, change WTHR to WTHRMIN = PMAX, set Bit 0 (TERMSEL1[0]) to 1, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register, read the CF1 pin frequency and compare it to the desired CFREF.
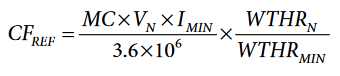
AWATTOS is then the signed 24-bit representation of the following:
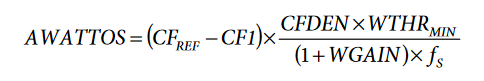
Repeat the procedure to determine BWATTOS by setting Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 1, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register. To determine CWATTOS, set Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 1 and repeat the procedure.
Total and Fundamental Reactive Energy Calibration
The total and fundamental reactive energy calibration is not necessary because the gains and offsets computed for the total active energy should be the same: AVARGAIN and AFVARGAIN are equal to AWGAIN, and AVAROS and AFVAROS are equal to AWATTOS, and so on. However, for outstanding accuracy, the total and fundamental reactive energy can be calibrated using the same procedures presented for the total active energy calibration in the Calibration of the WGAIN Registers section and Calibration of the WATTOS Registers section. The only difference is that the currents and voltages must have a power factor of 0 (the current has a delay of 90° relative to the voltage on the same phase).
Aparent Energy Calibration
Calibration of VAGAIN Reisters
The gains computed for the apparent energy should be the same with the gains computed for the total active energy; AVAGAIN, BVAGAIN, and CVAGAIN should be respectively equal to AWGAIN, BWGAIN, and CWGAIN. However, for outstanding accuracy, the apparent energy may be calibrated using the same procedure presented for the total active energy calibration in the Calibration of the WGAIN Registers section.
The apparent energy data path does not contain any offset compensation registers because the offset is compensated in the rms data path using the xIRMSOS and xVRMSOS registers.
Reference Meter Method
Current and Voltage RMS Calibration
To calibrate the current and voltage rms, use the accurate source method. See the Current and Voltage RMS Calibration section for additional information.
Total and Fundamental Active Energy Calibration
To perform the total active energy calibration, execute the following:
- Power up the ADE7878.
- Configure the ADE7878 to provide pulses proportional to the Phase A, Phase B, and Phase C total active energy at the CF1, CF2, and CF3 pins, respectively
- Supply the meter with nominal phase voltages, nominal phase currents, and phase power factors equal to 1.
- Calibrate the AWGAIN, BWGAIN, and CWGAIN registers
- Supply the meter with nominal phase voltages, nominal phase currents, and phase power factors equal to 0.5.
- Calibrate the APHCAL, BPHCAL, and CPHCAL registers.
- Supply the meter with nominal phase voltages, minimum phase currents at which the meter must be certified, and phase power factors equal to 1.
- Calibrate the AWATTOS, BWATTOS, and CWATTOS registers.
The fundamental active energy calibration is not necessary because the gains and offsets computed for the total active energy should be the same; AFWGAIN is equal to AWGAIN, AFWATTOS is equal to AWATTOS, and so on. However, for outstanding accuracy, fundamental active energy can still be calibrated using the same procedures presented in Total and Fundamental Active Energy Calibration section.
Calibration of the WGAIN Registers
As previously stated, the calibration of gain registers is necessary to compensate for small amplitude errors determined by the current transformers, resistor dividers, and the ADCs. The procedure to calibrate AWGAIN, BWGAIN, and CWGAIN is as follows:
- Supply each phase of the meter with nominal current, nominal voltage, and a power factor of 1 (0° delay between the current and voltage on the same phase).
- Set Bit 0 (TERMSEL1[0]) to 1, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register, so that only Phase A powers are provided at the CF1 pin.
- Set the CF1 pin to provide signal proportional to the sum of the total phase active powers by initializing Bits[2:0] (CF1SEL[2:0]) in the CFMODE register to 0.
- Read the CF pin frequency of both meters: the one to calibrate (CF1) and the reference one (CFREF). Repeat this operation multiple times and use the arithmetical average in Equation 5.
AWGAIN is the signed 24-bit hexadecimal representation of the following:

Repeat the procedure to determine BWGAIN by setting Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 1, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register. To determine CWGAIN, set Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 1 and repeat the procedure.
Calibration of the PHCAL Registers
As previously stated, the phase calibration is necessary to compensate for the phase delay introduced by the current transformers. The procedure to calibrate the APHCAL, BPHCAL, and CPHCAL registers is as follows:
- Supply each phase of the meter with a nominal current, nominal voltage, and power factor equal to 0.5 inductive (the current has a delay of 60° relative to the voltage on the same phase).
- Use the same initializations as the Calibration of the WGAIN Registers section.
- Read the CF frequency of both meters: the one to calibrate (CF1) and the reference one (CFREF). Repeat this operation multiple times and use the arithmetical average in Equation 6.
- Compute the angle representing the delay error between the phase current and phase voltage by:
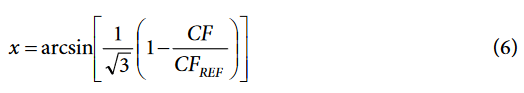
The phase resolution of the timer used to compensate the phase delay is:
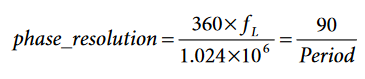
where:
FL is the line frequency of the system.
Period is the ADE7878 register indicating the line period of the phase voltage.
Divide x by phase_resolution and compute the APHCAL number:
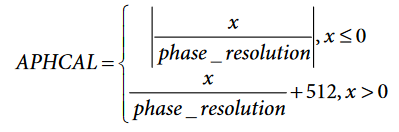
Note that the previous expressions imply x is obtained in degrees. If x is obtained in radians, then the phase resolution formula changes to:
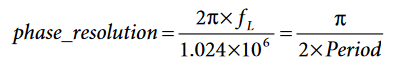
Repeat the procedure to determine BPHCAL by setting Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 1, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register. To determine CPHCAL, set Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 1 and repeat the procedure.
If the phase errors in the system were large, they may introduce gain errors that are not compensated for during the WGAIN calibration. In this case, after the phase errors are compensated for, gain calibration must be executed one more time to eliminate these potential errors.
Calibration of the WATTOS Registers
As previously stated, the offset compensation is necessary to compensate for the effect of the correlated noise present in the data paths. The procedure to calibrate AWATTOS, BWATTOS, and CWATTOS is as follows:
- Supply each phase of the meter with the minimum current for which the desired accuracy is required, with the nominal voltage and a power factor of 1 (0° delay between the current and voltage on the same phase).
- Set the WTHR register equal to WTHRMIN = PMAX to increase the frequency at the CF1, CF2 and CF3 pins, now that the phase current is small, which decreases the calibration time significantly.
- Set Bit 0 (TERMSEL1[0]) to 1, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register so only Phase A powers are provided at CF1 pin.
- Set the CF1 pin to provide signal function of the phase total active powers by initializing Bits[2:0] (CF1SEL[2:0]) in the CFMODE register to 0.
- Read the CF frequency of both meters: the one to calibrate (CF1) and the reference one (CFREF). Repeat this operation multiple times and use the arithmetical average in the following expression.
The AWATTOS is the signed 24-bit hexadecimal representation of the following:
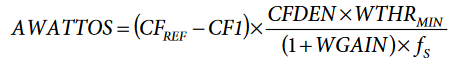
where fS is 8 kHz, the sampling frequency of the ADE7878.
Repeat the procedure to determine BWATTOS by setting Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 1, and Bit 2 (TERMSEL1[2]) to 0 in the COMPMODE register. To determine CWATTOS, set Bit 0 (TERMSEL1[0]) to 0, Bit 1 (TERMSEL1[1]) to 0, and Bit 2 (TERMSEL1[2]) to 1 and repeat the procedure.
Total and Fundamental Reactive Energy Calibration
The total and fundamental reactive energy calibration is not necessary because the gains and offsets computed for the total active energy should be the same; AVARGAIN and AFVARGAIN are equal to AWGAIN, AVAROS and AFVAROS are equal to AWATTOS, and so on. However, for outstanding accuracy, total and fundamental reactive energy can still be calibrated using the same procedures presented for the total active energy calibration. The only difference is that the currents and voltages must have a power factor of 0 (the current has a delay of 90° relative to the voltage on the same phase).
As a reference, execute the following operations:
- Configure the ADE7878 to provide pulses proportional to the Phase A, Phase B, and Phase C total reactive energy at the CF1 pin by initializing Bits[2:0] (CF1SEL[2:0]) in the CFMODE register to 001. To calibrate the fundamental reactive energy, initialize the same bits to 100.
- Calibrate the A(F)VARGAIN, B(F)VARGAIN, and C(F)VARGAIN registers using the procedure outlined in Calibration of the WGAIN Registers section.
- Calibrate the A(F)VAROS, B(F)VAROS, and C(F)VAROS registers using the procedure outlined in Calibration of the WATTOS Registers section.
Apparent Energy Calibration
Calibration of the VAGAIN Registers
Calibration of the VAGAIN Registers The gains computed for the apparent energy should be the same as the gains computed for the total active energy; AVAGAIN, BVAGAIN, and CVAGAIN should be equal to AWGAIN, BWGAIN, and CWGAIN, respectively. However, for outstanding accuracy, the apparent energy can still be calibrated using the same procedures presented for the total active energy calibration. As a reference, execute the following operations:
- Configure the ADE7878 to provide pulses proportional to the Phase A, Phase B, and Phase C total apparent energy at the CF1 pin, respectively, by initializing Bits[2:0] (CF1SEL[2:0]) in the CFMODE register to 010.
- Calibrate the AVAGAIN, BVAGAIN, and CVAGAIN registers using the procedure outlined in Calibration of the WGAIN Registers section.
The apparent energy data path does not contain any offset compensation registers because the offset is compensated in the rms data path using the xIRMSOS and xVRMSOS registers.
Hexadecimal Computation
Computing Hexadecimal Representation of a Signed Fractional Number
Many calibration registers of the ADE7878 are 24-bit signed numbers. The hexadecimal representation, X, of a positive number x lower than +1 is X = x × 223.
The hexadecimal representation, X, of a negative number greater than −1 is X = 224 + x × 223.
Computing Hexadecimal Representation of THR Thresholds
The WTHRx, VARTHRx, and VATHRx registers are 48-bit registers accessed as two 32-bit registers, xTHR1 and xTHR0 (x = W, VAR, or VA), each having eight most significant bits (MSB) padded with zeros. To compute xTHR1 knowing THR, the following expression is used:
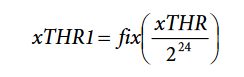
The function fix means the result of the division between xTHR and 224 is rounded down to the nearest positive integer.
To compute xTHR0, the following expression is used:
xTHR0 = xTHR − xTHR1 × 224
