非線形回路ハンドブック
第三章 非線形回路を理解する
このページの目次
- トランスコンダクタンス乗算器
- 2 象限乗算器
- 4 象限乗算器
- 4 象限トランスコンダクタンス乗算器の性能
- トランスコンダクタンス乗算器の精度に影響を与える要素
- 非線形誤差
- トランスコンダクタンス乗算器の動特性
- トランスコンダクタンス乗算器の線形化
トランスコンダクタンス乗算器
可変トランスコンダクタンス乗算器は、少なくとも概念的には最も単純なタイプのアナログ乗算器です。一方の入力変数は能動デバイスのゲイン(トランスコンダクタンス)を制御し、これにより、制御入力に比例して他方の入力を増幅します。
アナログ・コンピューティング用および通信用信号処理のための「トランスコンダクタンス」(あるいは「トランスレジスタンス」)乗算器と変調器を作成するために、トランジスタ、FET、真空管などのさまざまな能動デバイスが使われてきましたが、それらの成功の度合はそれぞれ異なります。しかし、現在提供されている「トランスコンダクタンス」乗算器のほとんどすべてが、能動素子としてシリコン接合トランジスタを使用しています。これは、トランジスタのコレクタ電流とトランスコンダクタンスの間に、式(16)に示す線形の一貫した関係が成り立つためです。

ここで、
Ic = コレクタ電流(A)
Vbe = ベース・エミッタ電圧(V)
q = 電荷の単位 = 1.60219 x 10-19 クーロン
k = ボルツマン定数 = 1.38062 X 10-23 joules/°K
T = 絶対温度(°K)= °C + 273.15°
q/kT = 25 °C で 1/(25.69 mV)
乗算器としての特性は、増分 ∆Ic、∆Vbe(図 7)が十分に小さい場合に見ることができます。

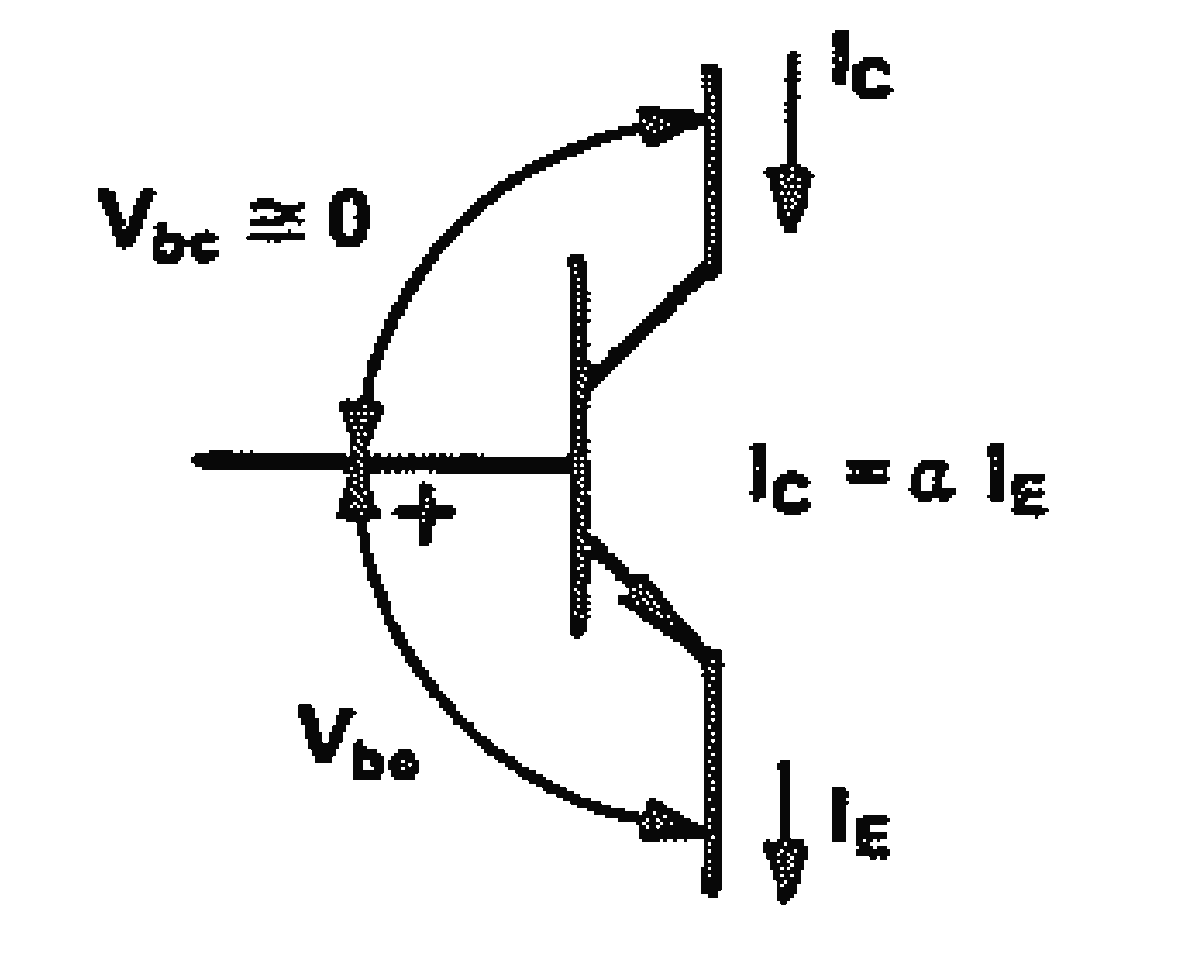
式(16)は、下に示す簡略化した接合部の式を微分することによって得られます*。

αN = 電荷移動係数 ≈ 0.99
IES = エミッタ飽和電流、10-12 ~ 10-14 A @25℃
この時、トランジスタのコレクタ・ベース電圧はゼロと仮定します。
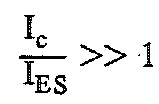
それでも電流レベルは十分に低いので、オーム抵抗(たとえば、ベース拡散抵抗、エミッタ・コンタクト抵抗、およびバルク抵抗)は無視できます。代表的なモノリシック・デュアル・トランジスタでは、これはコレクタ電流が 100 µA 以下であることを意味します。100 µA の場合、トランスコンダクタンスは 26 °C で約 1/260 mho です。モノリシック・トランジスタの代表的な寄生抵抗値は約 3 Ω ですが、これは、トランスコンダクタンスを約 1 % 減少させます。
簡単な 2 象限可変トランスコンダクタンス乗算器は、図 8 に示すように、1 対のトランジスタといくつかの抵抗を使って構成できます。この乗算器の出力を Q1 と Q2 のコレクタ電流の差と見なすと、この回路の出力と入力の関係は式 19 と 20 で表されます。
* 3-1 項の式(6)を参照。
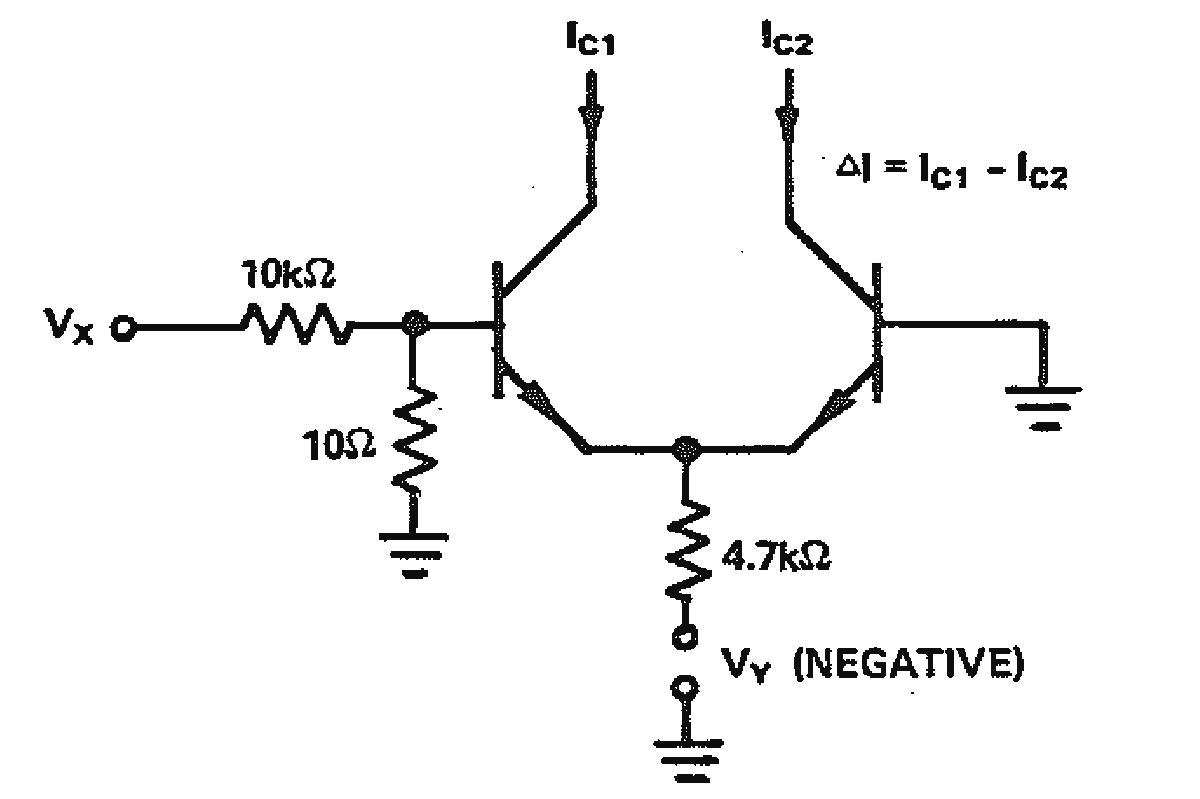
式(20)が示すように、出力のコレクタ電流の差は、入力電圧 Vx と Vy の積に比例しますが、以下の制約があります。
- Y 入力には、Q1 と Q2 の仮定された(一定の)VBE による 0.6 V のオフセットがあります。したがって、受け入れ得る Vy の最も正側に近い値は -0.6 V です。また、Vbe は一定ではありません。Q1 と Q2 の Vbe は |Vy| の増加に伴って増加し、Y 入力に非線形性を生じさせます。これらの問題は、Y 入力の抵抗に代えて、より精巧な電圧電流コンバータを使用することによって解決できます。
- スケール・ファクタは温度の関数で、25 °C 付近では -0.33 %/ °C の率で減少します。これは、X 入力に温度補償抵抗を使用することで解決できますが、精密な補償を行うことは困難です。
- 式(18)に示すようにコレクタ電流とベース・エミッタ電圧は指数関係にあるので、X 入力は非線形です。X 入力に 1000:1 の減衰器を使用すれば ±10 V のレンジが 2 つのベース間で ±10 mV になるので、実際の X 信号は熱電圧 kT/q(25.69 mV @25 °C)未満になります。ただし、この小さい信号でも X 入力信号には 7 % の非線形性が生じます。この非線形性は X 入力の減衰を大きくすることによって小さくできますが、代償として S/N 比が減少してしまいます。
以上のような理由から、差動ペアは、高レベルのアナログ乗算器として特に有用、あるいは魅力的というわけではありません。しかし、受信信号がすでに十分に小さい(数ミリボルト以下)RF アプリケーションのミキサーとしては、極めて有効です。
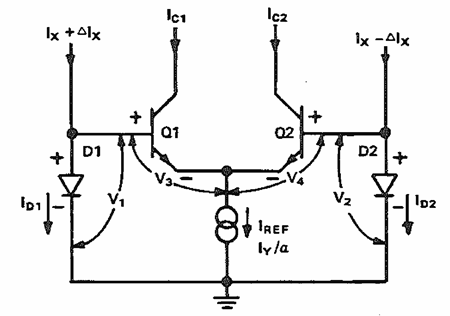
非線形性、ダイナミック・レンジの制約、温度係数など、簡単な差動ペアの問題点に対しては、適切かつ本質的に単純な解決策があります1。ギルバート回路は、誤差が少ない(約 1 %)上に帯域幅が広く(>100MHzが可能)、しかも比較的単純なので、短期間に広く使われるようになりました。実際、今では「トランスコンダクタンス」乗算と同義語になっています。図 9 に示す基本回路は、ダイオード(またはダイオード接続したトランジスタ**)の指数特性を使って、差動ペアのベース入力(以後、便宜上「X」入力と記します)の指数非線形性を補償します。
バランスが取られた X 入力電流 ID1 と ID2 がダイオード D1 と D2 を通過して、電圧 V1 と V2 を発生させますが、これらの電圧は電流の対数に比例します(αN ≈ 1)。

1 "A new Wide-Band Amplifier Technique," by Barrie Gilbert, IEEE Journal of Solid-State Circuits.December, 1968, Volume SC-3, No. 4, pp. 353-365.
Q1 と Q2 のコレクタ電流はそれらのベース・エミッタ電圧(式 18)または差動入力電圧(VBE1 - VBE2)の指数関数なので、D1 と D2 によって与えられる対数入力電圧が、Q1 と Q2 の指数非線形性をすべてではないにしてもある程度相殺し、結果として ID1、ID2 と IC1、IC2 の関係は線形になると仮定することは合理的です。実際、線形化は理論的には完璧であり、実際の回路でもほぼ完璧で、驚くほど有用な結果が得られます。これは、以下のように証明できます。
仮定:
- IC1 = IC2 および ID1 = ID2 の場合、Q1、Q2 および D1、D2 のペアの差動オフセット電圧はゼロ。
- Q1、Q2、D1、D2 は理想接合部の式(18)に従う。
D1 の陰極から Q1、Q2、さらに D2 の陰極へと続くループの周りの電圧 V1 ~ V4 の合計は、ゼロでなければなりません。

Q1、Q2 のベース・エミッタ電圧は、そのコレクタ電流の対数に比例します。

これらを(24)の V1 ~ V4 に代入します。

kT/q 項を削除して対数の差を比の対数として書き直すと、次式が得られます。

すでに仮定したように、トランジスタとダイオードのマッチングが取られていれば定数はすべて同じで、次式が得られます。

比の対数が等しいなら、比も等しくなければなりません。

この結果は重要で、「出力」電流 IC1 と IC2 の比は、温度や電流の大きさに関わらず、入力電流 ID1 と ID2 の比に比例することを示しています。つまり、概念的には線形化は完璧であり、X の入力から出力への伝達特性は温度によらず一定です。
乗算器の関係は(30)から直接導くことができます。X 入力は、2 つのダイオード電流 ID1 と ID2 の差 2∆Ix であると仮定します。Y 入力がエミッタ電流 IREF を制御します。乗算器の出力は、Q1 と Q2 のコレクタ電流の差 2∆IC です。

Q1、Q2 および D1、D2 は整合していると仮定し、Q1 と Q2 は高い β 値(> 100、α ≈ 1)を有しています。

これを(29)の IC と ID に代入します。

さらに代数的に整理すると、次式が得られます。

出力電流は、X 入力の差分電流 ∆IX と Y 入力の電流の積に比例し、X の静電流 IX に逆比例します。 IX は、2 象限乗算器(バイポーラ ∆X 入力とユニポーラ Y 入力)としてのスケール・ファクタを決定していると見ることができます。この回路は 2 象限除算器としても機能し、この場合は Iy が一定、分母(IX)がユニポーラ、分子(∆IX)がバイポーラです。この線形化乗算器(図 9)は非常に優れた性能を備えており、以下の点で、単純な差動乗算器よりも大幅に改善されています。
- 広い帯域幅: 回路は基本的に「電流モード」です。数 mA の電流レベルでは、100 MHz を超える帯域幅が得られます。乗算器で通常使われる低い電流レベル(< 1 mA)では、1 ~ 10 MHz の帯域幅が容易に得られます。
- 優れた線形性: 式(39)は、入力と出力の関係が正確に乗算であることを示しています。実際には多少の誤差(< 1 %)がありますが、これについては後述します。
それでも、線形化されていない乗算器より大きく改善されています。
- 優れた温度安定性: 式(39)は、入力と出力の関係が温度に依存しないことを示しています。実際の回路にはわずかな温度依存性があり、その一部は温度によるトランジスタの β の変化によります(β の影響は無視できると仮定して(39)を導き出しました)。温度に伴うゲイン変化は 0.02 %/ °C 以下に抑えることができますが、これは、単純な差動乗算器(0.3 %/ °C)より 1 桁以上改善されています。
- 広いダイナミック・レンジ: X(ベース)入力が線形化されているので、ほぼ -Ix < ∆Ix < Ix と等しい範囲にわたって X 入力電流の比を変化させることができ、差動ペアよりはるかに大きい入力信号を使うことができます。
これらの利点の結果として、線形化された「ゲイン・セル」が、乗算器の汎用ビルディング・ブロックとしてほぼ例外なく受け入れられるようになりました。これは、わずかに変更を加えると、2 象限乗算回路として直接使用できます。
2 象限乗算器
図 10 の回路は、実際に機能する 2 象限乗算器の例です。差動 X 入力電流は、抵抗 R1 によってエミッタを結合した差動ペア Q6、Q7 から得られます。定電流源 Q8、Q9 は、Q6、Q7 のエミッタに Ixバイアスを提供します。100 kΩ のエミッタ抵抗 R1 は、入力電圧 Vx 1 ボルトあたりの差動 X 電流 ∆Ix を決定します。
X 入力電流は、図 9 の回路のようにコレクタ(つまり陽極)を駆動するのではなく、ダイオード接続トランジスタ** Q2A と Q2B のエミッタを駆動します。この「反転」接続はエミッタが低インピーダンスで、X 入力段 Q6、Q7 からの電流をいつでも受け入れることができるので、駆動がずっと容易です。「反転」回路と基本電流セルの実用上の唯一の違いは、出力も反転することです(つまり入力と 180° 位相がずれます)。
これは、出力アンプの位相を正しく設定することによって、簡単に修正できます。
Y 入力電流は、クローズド・ループ制御された電流源 A1-Q5 から得られます。Q5 のβ が非常に高い(> 400)場合は Q5 のコレクタ電流が Vy/R2 となります。誤差は無視できる程度です。ダイオード D1 は、Y の入力電圧が正になった時に、Q5 のベース・エミッタ接合がブレークダウンを起こさないように保護します。差動出力電流(Q1A-Q1B のコレクタ間)は、ダイナミック・ブリッジ R3、R4、R5、R6、および A2 によってシングルエンド電圧に変換されます。これらの抵抗は、Y 入力信号に伴う同相入力電圧の変化による出力電圧誤差を最小限に抑えるために、極めて正確に(0.1 %)整合していなければなりません。
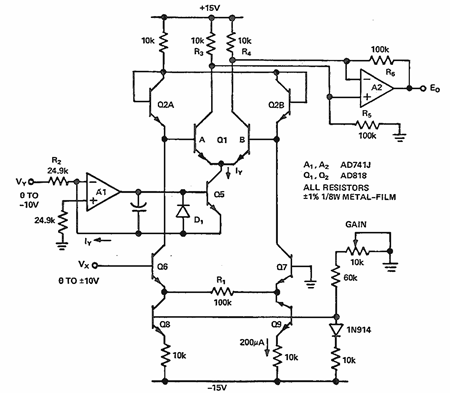
2 象限乗算器は、1 つの入力のフィードスルーを非常に低くする必要がある場合、特に有用です。Y 入力がゼロの状態では、出力は入力から実効的に切断されて、X 入力信号を少なくとも 80 dB 減衰します。
この利点には欠点が伴います。Y入力が小さくなると、Q1A と Q1B の電流が減少して回路の帯域幅が狭くなります。
4 象限乗算器
基本的な 2 象限線形化乗算器回路は、X 入力または Y 入力のどちらにもバイポーラ信号を受け入れて、4 象限で動作するように拡張できます。これは、2 番目の差動ペア Q3A-B を追加することによって実現されます。追加差動ペアのベースは、図 11 に示すように Q1 のベースと並列に接続します。追加ペアのコレクタは Q1A-B のコレクタにクロス接続します。2 象限乗算器のシングルエンド Y 電流源は、X 電流源と同じ差動電流源 Q10、R2、Q11 に置き換えられます。
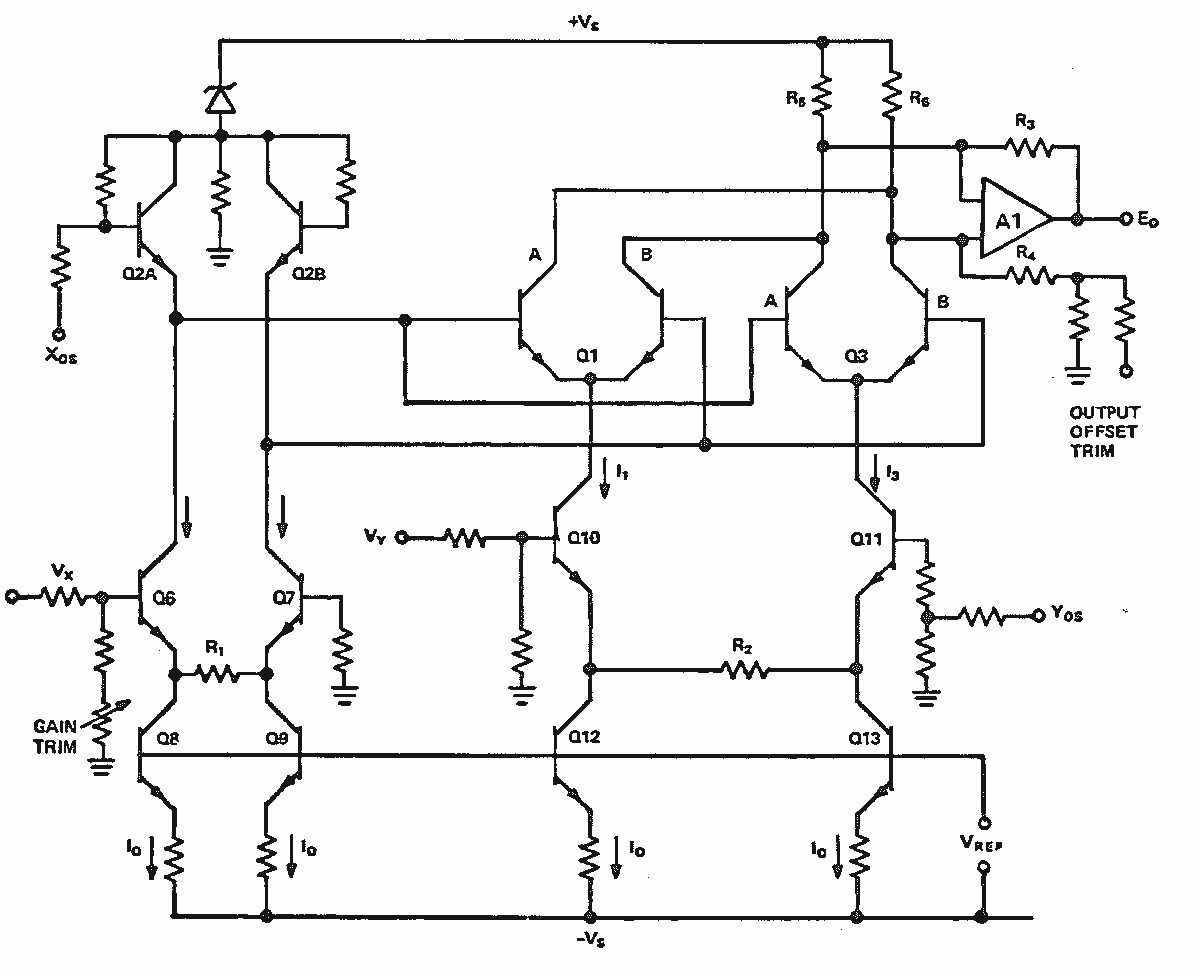
2 つある Y 電流源の一方の出力は Q1A-B のエミッタに、もう一方は Q3A-B のエミッタに接続されています。したがって、Vy は差動ペア Q1A-B を流れる電流と Q3A-B を流れる電流の比を変化させ、それらの相対ゲインを制御します。例えば、Y = 0 の場合は I1 = I3 となり、2 つのペアのゲインが等しくなります。これらのペアのコレクタはクロス結合されていて(ベースは並列)出力が相殺されるので、X 入力の信号の正味ゲインはゼロです。この「バランス」状態では、Vy = 0 の場合、X 入力はヌル化されます。

Y 入力にゼロ以外の電圧が加わると、電流 I1 と I3 はアンバランス状態になります。

このアンバランス状態により、2 つのペア Q1A-B と Q3A-B のゲインはもはや相殺されないので、X 入力信号が乗算器の出力に現われます。Y 入力が正の場合は I1 が I3 より大きくなって Q1A-B のゲインが優勢となるので、正の出力電圧が生じます(正の X に対して)。これに対し、Y 入力が負の場合は Q3A-B のゲインが優勢となり、正の X 入力に対しては負の出力電圧が、負の X 入力に対しては正の出力電圧が生じます。
Y 入力から出力への信号伝達動作は、2 象限乗算器での動作に似ています。X 入力がゼロで、Q1、Q2、Q3 の各トランジスタ・ペアが整合していれば、Q1A-B の側と Q3A-B の側の間で電流 I1 と I3 の変化が均等に分割されるので、Y の値に関わらず出力はゼロになります。

乗算器の全体的な出力と入力の関係は、以下のように(39)から導くことができます(I0 = Ix)。Q1A-B の出力は次式で表されます。

同様に、Q3A-B については次式が成り立ちます。

Q1A-B と Q3A-B のコレクタはクロス結合されているので、出力電流が差し引かれます。差は ∆IC です。

(41)と(42)から I1 と I3 を代入すると、次のようになります。

さらに、I10 = I30 なので、次式が得られます。

正味差動出力電流は、2 象限乗算器の場合と同様に、A1 と R3、R4、R5、R6 によってシングルエンド出力電圧に変換されます。

(50)は次のように整理することができます。

乗算器のスケール・ファクタは R3/R1R2I0 によって設定され、求められれる次元 V-1 になります。
4 象限トランスコンダクタンス乗算器の性能
可変トランスコンダクタンス乗算器の全体性能は優れたものであり、電子アナログ乗算器の最も一般的なタイプとなっています。ギルバート型線形化乗算器の成功の理由は 3 つあります。
- 良好な精度: フルスケールの ±1 % 未満の全体誤差(10 V で 100 mV)を簡単に実現できます。誤差は入力レベルに比例し、入力がゼロに向かうと誤差もゼロに近付きます(ゼロに調整可能な DC オフセットを除く)。実際に、「非線形」誤差の最大値は簡単な線形方程式で示すことができます。

ここで、
єx = X 入力の規定された非線形性( %)
єy = Y 入力の規定された非線形性( %)
- 広い帯域幅: 電圧出力乗算器で最大 10 MHz、電流出力で 100 MHz 以上。帯域幅が 10 MHz 未満の場合、帯域幅は信号レベルや入力パス(X または Y)には依存しません
- 比較的単純で低価格: 可変コンダクタンス乗算器は、「ディスクリート」部品を使って構成するか、「モノリシック」で作成することができます。いずれの場合も、本質的に回路が単純で一定した性能が得られるので、他のいかなる 4 象限乗算器より低価格です。以降ではこれらの要素についてより詳しく解説し、実際の回路や部品の要件に関連付けていきます。
トランスコンダクタンス乗算器の精度に影響を与える要素
これまでの可変トランスコンダクタンス乗算器の説明では、トランジスタが理想接合方程式に従い、トランジスタが完璧に整合しており、電流ゲインが無限大であると仮定しました。また、対称パス内の電流は、信号の注入によって生じる違いを除き、すべて等しいと仮定しました。実際の回路では、トランジスタや抵抗は「理想的」ではなく、完璧に整合することは(まず)決してありません。これらの不整合や「理想」動作からのずれは、線形誤差(入力および出力オフセット、スケール・ファクタ誤差)や非線形誤差(2 次および 3 次高調波歪み)を発生します。
この章の冒頭で示したように、線形誤差は理論的にはゼロに調整可能で、実際の回路でも無視できるレベルにまで調整することができます。図 11 には 4 つのトリム・ポイントが示されています。
- X オフセット: 線形 Y フィードスルーをゼロに調整するために使用します。
- Y オフセット: 線形 X フィードスルーをゼロに調整します。
- 出力オフセット
- スケール・ファクタ、つまりゲイン。
非線形誤差
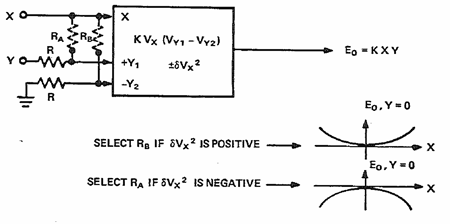
可変トランスコンダクタンス乗算器における非線形の主な発生源は、2 つの差動ペア Q1A-B と Q3A-B の間の電流のアンバランスか、オフセット電圧の不整合です。これらのペアのオフセット間に 500 µV の不整合があると、X 入力に(フルスケールの)1 % の非線形性とフィードスルーが生じます。図 12 に示すように、この非線形性は V2x に比例します。幸い、ディスクリート回路では特性の近いものをペアに組むことができ、集積回路内では「同じ」トランジスタをレイアウトすることができるので、平均オフセットの不整合が 500 µV 未満の場合、X の非線形性は通常 1 % 未満です。
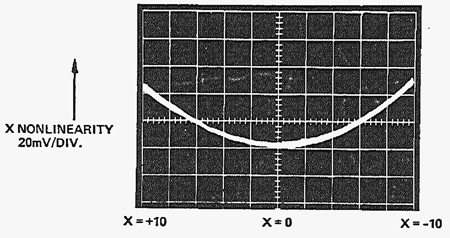
X の2 次非線形性は Y の入力信号振幅にはあまり依存しないので、以下に説明するように、X2 で表される非線形性は、X 入力信号の一部を Y 入力にクロス結合することによって大幅に減らすことができます。
X2 で表される非線形性のもう 1 つの発生源として考えられるのは、Vx = 0 の時に、ダイオード接続トランジスタ** Q2A と Q2B を流れる電流のアンバランスです。これらの電流は、正確に整合した抵抗を X の電流源に使用することによって等しくすることができます。
図 13 に示すように、X 入力は、ある条件下では著しい 3 次(S 字形)の非線形性を示すことがあります。3 次歪みは、差動ペア QIA-B と Q3A-B のエミッタ抵抗のオーミック成分によって生じます。
オーミック(定)抵抗は、qIc/kT の理論値からトランスコンダクタンスを減少させて、非線形性を生じさせます。高速乗算器は高電流で動作するので、オーム抵抗によるこれらの非線形性のために速度と精度のトレードオフが避けられなくなると見なされます。
トランスコンダクタンス乗算器の Y 入力の非線形性は比較的小さく、通常 ±0.1 % ~ ±0.2 % です。差動ペア Q1A-B と Q3A-B のオフセット電圧の不整合と、初期 Y 入力電流のアンバランスが Y の非線形性とフィードスルーに与える影響は無視できる程度であり、常に低い値を示します。
エミッタ抵抗が kT/qIc(Ic = 1 mA で 26 Ω、T = 300°K)と比べて大きくない場合、差動電流コンバータへの X と Y の入力電圧は、非線形性を生じる可能性があります。
トランスコンダクタンス乗算器の動特性
トランスコンダクタンス乗算器は基本的に電流モード回路なので、帯域幅が広く、過渡応答が高速です。100 MHz 以上の電流出力帯域幅は、乗算器のトランジスタを 10 mA 以上のエミッタ電流で動作させることによって実現できます。しかし、最良の DC 精度を得るために設計された回路は、これよりずっと低い 10 µA ~ 1 mA の電流で動作し、帯域幅は 1 ~ 10 MHz です。帯域幅の制限は主に出力アンプによるもので、このアンプはコレクタ電流の差を出力電圧に変換します。
4 象限可変トランスコンダクタンス乗算器の帯域幅は X または Y 入力に関して同じであり、出力アンプのスルーレートの制限を除き、信号レベルには依存しません。
トランスコンダクタンス乗算器の線形化
図 11 の 4 象限可変トランスコンダクタンス乗算器回路で顕著なのは、上に述べた理由から、X 入力の 2 次非線形性とフィードスルーです。Y 入力の非線形性は、通常、「X 」の歪みに比べると無視できる程度です。すべての 1 次誤差(線形フィードスルー、出力オフセット、スケール・ファクタ誤差)をゼロに調整した場合、乗算器の入力と出力の関係は、次式により高い精度で近似できます。

非線形項 δV2xf(Vy)が Vy に依存しない場合(あるいは大きく影響されない場合)は、図 14 に示すように X 入力信号の一部を Y 入力に加えるか Y 入力から引くことによって、δV2x の非線形性を相殺することができます。
幸い、δX2 の非線形性が Y 入力に大きく影響されることはないので(つまり f(Y)はほぼ一定)、この相殺方法は実際の回路でも比較的良好に機能します。通常、フィードスルーの X2 成分(Y = 0)はフルスケールの 0.1 % 未満まで減らすことができ(60 dB でゼロに抑制)、X の非線形性(Vy = 10 V)は半分に減らすことができます。それに応じて、全体の誤差が減少します。
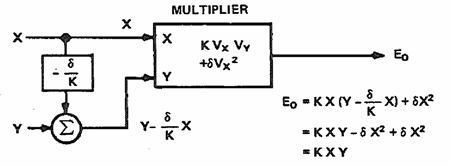
乗算器に X の線形化を適用する方法を図 15 に示します。この方法は、ソース抵抗がかなり低い(100 Ω 以下)ことと、正負両方(差動)の Y 入力が与えられていることに依存しています。多くの乗算器では(例えばアナログ・デバイセズのこのタイプの乗算器)、Y0 トリム端子を線形化回路の -Y 入力として使用できます(ただし必ずしも同じ感度ではありません)。
乗算器に対して線形化を行った結果を図 16 ~ 18 に示します。低周波数と高周波数両方のフィードスルーが減少している点に特に注意してください。
Y 入力にはクロス結合による線形化手法を適用できますが、Y の非線形性は何もしなくても一般に非常に小さいので、「収穫逓減の法則」(効果の低減)が当てはまります。
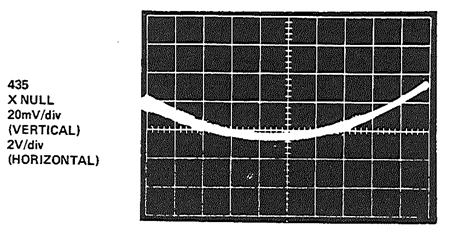

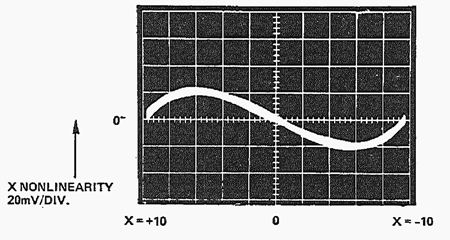
図16: トランスコンダクタンス乗算器の X の線形化の効果(X = ±10 V、Y = 0、垂直スケール 20 mV/div.)
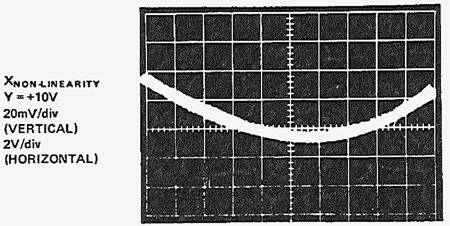

図 17: 図 16 と同じ乗算器の X の線形化の効果(X = ±10 V、Y = +10 V、垂直スケール 20 mV/div.)
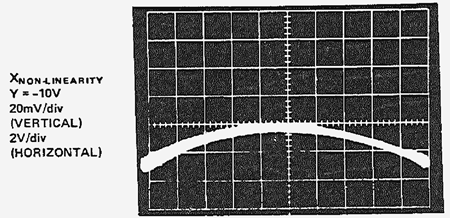
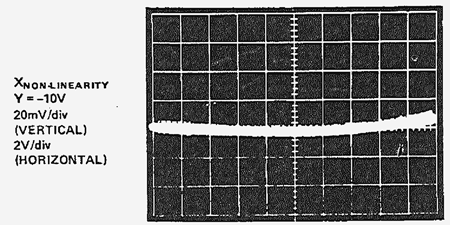
図 18: 図 16 と同じ乗算器の X の線形化の効果(X = ±10 V、Y = -10 V、垂直スケール 20 mV/div.)
クロス結合線形化手法は、一方または両方の入力に 2 次非線形性があるあらゆる乗算器に適用できます。全体の誤差の減少量は、一方の入力の非線形性が他方の入力の信号レベルからどの程度独立しているのかによって異なります。
一般に、一方の入力の 2 次非線形性を完全に相殺できるのは、他方の入力がある特定の値になった場合だけで、その値は 1 つしかありません。例えば、X のフィードスルーの 2 次成分(X = ±F.S、Y = 0)は完全に相殺することができますが、X の 2 次非線形性はその一部しか相殺することができず、場合によっては増加してしまうことさえあります。
非線形回路ハンドブックのPDFを無料でダウンロード

この技術書は、Analog Devices社の"Non-Linear Circuit Handbook"を和訳したものです。
非線形アナログ回路の原理、性能、仕様、テスト、応用に関する情報が1冊にまとまっています。50年以上前に考案された半導体の非線形特性を利用した回路は、最新の信号処理用の集積回路の中に隠れて、数多く使われています。
非線形回路の詳細を理解することで、それらを応用した新しい集積素子実現のもとになることを願っています。