非線形回路ハンドブック

このページの目次

• 乗算器
• 乗算の手法
• 乗算の特性
• 実際のアナログ乗算器の誤差

乗算器

アナログ乗算器は、2 つまたはそれ以上の独立した入力電圧または電流の積に比例する出力電圧または電流を生成するデバイスです。

比例定数 1/V_r の次元は V^-1 です。V_r は、回路内の特定の電圧または電流を使って確認するか、単独で決定することができます。通常は 10 V に固定されます。

乗算器の動作範囲は入力によって定めることができます。2 入力で各入力が 2 つの極性を取り得る場合、極性の組み合わせは 4 種類です。これは、X-Y 平面の 4 つの象限として図示できます（図 1）。

 

 

動作領域内の入力ペアは、乗算器の出力電圧を一意に決定します。4 象限の組み合わせすべてを受け入れて適切な極性の出力を生成することのできる乗算器は、「4 象限乗算器」と呼ばれます。「2 象限」乗算器は一方の入力の ± 信号と、もう一方の入力の単極信号に応答します。例えば、±V_x と +V_y に応答する乗算器は、斜線で示された I 象限と II 象限からなる半平面で動作します。

1 象限乗算器は、1 つの象限のユニポーラ入力にだけ応答します。V_x と V_y の両方が正の値に制限されている場合、その乗算器は第 1 象限で動作します。乗算器の中には、適切な数の象限に応答しても出力の極性が反転しているものがあります。その式は E_O = -KV_xV_y です。単一象限内の 1 つまたは複数の入力に応答する乗算器は、前段に絶対値回路を置き、後段に符号絶対値出力回路を置くことによって、複数象限の演算に使用できます。この場合、出力の極性は入力の極性によって決まります（文面から受ける印象の通り手順は面倒ですが、一部の乗算型 D/A コンバータなどのデバイスでは一般的です）。入力と出力をオフセットすることによって、多象限動作を実現することもできます（図 21 参照）。

 

乗算の手法

現時点で、電子式アナログ乗算を行うための最も一般的な方法は、可変トランスコンダクタンスとパルス幅、パルス高変調の 2 つです。第 3 の方法である対数／逆対数法も普及しつつあり、特に低速高精度の計算によく使われています。

この章では、これら 3 種類の乗算器の回路設計と、全体的性能に影響を与える要素について詳しく説明します。

これまで、アナログ・コンピューティング、通信、および計測用の回路には他にも多くのタイプの乗算器と変調器が使われており、また、現在でも使われています。これらの例には、二乗差掛け算器、ダイオードリング、FET、磁気デバイス（例えばホール効果）などが含まれます。

ここではこれらのタイプの設計については触れませんが、仕様とテストに関する説明の大半は、これらにも当てはまります。

 

乗算の特性

乗算の代数的特性はアナログ乗算器の設計と仕様の決定的要素なので、これらの特性のいくつかと、それらの物理的乗算器性能との対応を改めて見直しておくと、理解を助けます。

設計や特性評価に直接影響する顕著な乗算特性の 1 つは、3 種類の入力の組み合わせで積がゼロになる事実です。

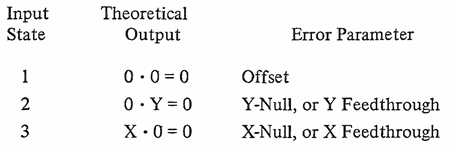
もう 1 つの重要な特性は、積の大きさと入力の関係です。ほとんどの一般的乗算器がそうであるように、両方の積が常に V_r より小さいと仮定すると（つまり、V_r がフル・スケール）、積は常に V_r 以下となります。

2 つの入力が等しくないと、（2）の条件が満たされる場合、その積は小さい方の入力より小さくなります。つまり、次の関係が成り立つとします。

および

この場合は次式が成り立ちます。

式 2 ～ 6 は、理想乗算器の出力は小さい入力で穏やかに動作することを示しています。どちらかの入力または両方の入力がゼロになると、出力もゼロになります。1次（線形）誤差がゼロに調整されていると仮定すると、本章で取り上げるアナログ乗算器回路は、この理想動作に驚くほど近い動作をします。その理由は、誤差の非線形成分（f（V_x, V_y））が V_x と V_y の連続関数で、V_x と V_y がゼロに減少するとこの成分もゼロになるからです。乗算器の誤差源、および回路設計と誤差の関係について説明している以下のセクションでは、その理由を示します。

乗算関数は、次の式を表す 3 次元の面で表わすことができます。

この面の形状は、以下の特性によって概要を示すことができます。

1.  X 軸および Y 軸に沿った出力（Z）はゼロです（フィードスルーがゼロ）。
2.  一方の入力が一定の場合、出力はもう一方の入力に直線的に比例し、勾配（ゲイン）は一定入力によって決まります。
3.  両方の入力が等しい場合（X = Y または X = -Y）、出力は入力の二乗に比例します。これは、極性が逆で互いに接する 2 つの放物線を、I-III の対角線と II-IV の対角線に対応する位置に直角に生成します。

 

これらの要件に適合する曲面は、図 2 に描かれている双曲放物面（鞍型曲面）です。放物線部分は、曲面と、対角線を通る垂直面および対角線に平行な垂直面との交線に相当します。（条件 3）。

直線要素は X 軸および Y 軸に平行な垂直面と曲面との交線で（条件 2）、曲面は X 軸と Y 軸および両軸の交点 0 に沿って X-Y 平面を通過します（条件 1）。

 

 

水平面と関数の交線は双曲線になります。つまり、コンター・マップは、対角線 I-III に沿って丘を登っていき、対角線 II-IV に沿って谷を下っていく一連の直角双曲線を示します（図 5）。

図で 1、2、3、4 と表示された曲面のコーナーは、各象限での乗算器の最大出力を表しています。これらの最大値は、±X と ±Y の 4 つの組み合わせに生じます。

乗算器は実際明らかに非線形ですが、乗算器を非線形デバイスとする考え方は矛盾しているように見えるかもしれません。結局、X または Y を一定値として動作させた乗算器のゲイン特性を実際に計測すれば、線形の出力／入力関係が得られるはずです。つまり、乗算器はゲイン KX の線形アンプとして動作します。実際のところ、通常、「線形」乗算器は（1）の理想的な関係に従うものと考えられています。

一方の入力を固定すれば乗算器は確かに線形デバイスであり、概念的には、固定ゲインのアンプで置き換え可能なのは明らかです。信号入力はゲインを変化させることはできないので、出力には信号が線形に再生されます。

両方の入力を変化させると、応答は確かに非線形です。例えば、X と Y の両方に同じ入力が与えられた場合、出力は入力の二乗に比例します。これは明らかに非線形の動作で、比例の基準にも重ね合わせの基準にも当てはまりません（1 ページ参照）。

これを幾何学的に解釈すると、双曲放物面は展開面、つまり、円筒や円錐のように直線要素から構成できる曲面です。

一方の出力を一定に保てば理想的なアナログ乗算器は線形デバイスになる、というのは役に立つ事実です。この事実により、デバイスの特性が本質的には非線形であるにも関わらず、実際の乗算器の動作の特性評価、調整、校正、および測定を、線形の観点で容易に行えます。

 

実際のアナログ乗算器の誤差

実際のアナログ乗算器の出力は、その入力の理論的積と異なります。一般にその差 є の大きさは予測困難ですが、次式で定義されます。

（11）に記号で示された誤差を、回路内の誤差源に直接関係する項に展開することは、乗算器回路の特性を検討する上で非常に有効です。アナログ乗算器には、4 つの主要な静的（つまり DC）誤差があります（動的誤差については後で、乗算器の仕様のセクションで説明します）。

これらの誤差の影響は、次式のように適用できます。

式を展開して項をまとめると次のようになります。

この長い一連の誤差項は、それぞれを個別に考えることによって整理できます。

項	説明	入力への依存性
KVxVy	真の積	一方の入力または両方の入力がゼロになると、積もゼロになる
∆KVxVy	スケール・ファクタ誤差	Vx、Vy = 0 でゼロになる

 

厳密に言うと以下の項には K+∆K を掛けますが、∆K と他の誤差の積は 2 次誤差であってほとんど問題にならないため、∆K の影響は無視することができます。

VxYOS	Y 入力の DC オフセットによる線形「X」フィードスルー	Vx に比例
VyXOS	X 入力の DC オフセットによる線形「Y」フィードスルー	Vy に比例
XOSYOS	X、Y の入力オフセットによる出力オフセット	Vx、Vy には依存しない
ZOS	出力オフセット	Vx、Vy には依存しない
F（X, Y）	非線形性	Vx と Vy の両方に依存。Vx、Vy、その累乗および 外積に依存する項を含む。

 

実際のアナログ乗算器の誤差 є（X,Y）は、実際の乗算器出力と理論値の差を表す曲面として可視化することができます。一般に、この誤差曲面は歪みや捩れがあって平坦ではなく、丘の多い田舎の地形に良く似ています。4 象限乗算器の仮想誤差曲面を図 3 に示します。グラフの高さ、つまり Z 座標が、次式で表される誤差 є（X,Y）を示しています。

ここで、

E_O = 乗算器出力電圧の測定値

V_x = X 入力電圧

V_y = Y 入力電圧

KV_xV_y = 理想出力電圧

є（X,Y）は、（13）の誤差項の和に相当する測定電圧です。

 

 

誤差曲面を使用してアナログ乗算器の静的誤差を記述するのは面倒に見えるかもしれませんが、これは（13）の個々の誤差成分の全体的な 3 次元的影響を可視化する最も簡単な方法です*。

例えば、「線形」X フィードスルー V_xY_OS の影響を考えます。Y_OS が小さい正の量だとすると、V_x が増加するにつれて乗算器の出力も比例して増加します。V_x が負になると、出力も負になります。この影響が Y 入力に依存しないのは明らかですが、これは、式 10 には V_xY_OS が追加誤差.として示されているためです。線形 X フィードスルーがあると、XY 平面を真横から見た図（図 4）に示すように、誤差面が Y 軸の周りに傾きます。

同様に、X オフセット（「線形」Y フィードスルー）があると、誤差面全体が X 軸周りに傾きます。DC オフセット X_OXY_OS + Z_OS の影響があると、面全体が Z（出力）軸に沿って上下に移動します。

*誤差曲面は主に可視化のための手段として使われます。これと、2 次元コンター表現（"iso-vers": iso は「等しい」、ver（ity）は「正確さ」の意）は、この目的のために使われています。しかし、誤差関数の形はユニットごとに、また、さまざまな調整段や熱環境ごとに大きく異なるので、誤差曲面は個々のデバイスのデータのコンパクト表現としてほとんど役に立ちません。

 

 

スケール・ファクタ ∆K の影響はそれだけで考えられますが、これは次式で定義される誤差曲面を生成します。

 

 

これは、乗算器出力 V_z = KV_xV_y を単純にスケールダウンしたものです。したがって、スケール・ファクタ誤差は図 2 に描かれているように双曲放物面になるはずですが、大きさはずっと小さくなります。図 5 は 2 次元コンター（Iso-ver）で表したものです。非線形性 f（X,Y）の影響は、公称値としては直線となる X 軸または Y 軸に平行な要素に曲率を生じさせます。つまり、XZ 平面または YZ 平面に平行な乗算器出力曲面を通る断面が、直線ではなくなります（図 6）。

 

 

以上をまとめると、2 入力アナログ乗算器には、「トリミング可能」な静的誤差源が 4 つあります。（13）を参照すると、これらは以下の通りです。

1. X の入力オフセット（線形 Y フィードスルー）
2. Y の入力オフセット（線形 X フィードスルー）
3. 出力オフセット
4. スケール・ファクタ誤差

これら 4 つの誤差の影響は、誤差 1、2、3 に対して大きさが同じで極性が逆のオフセットを導入することによって、さらに 4 に対してスケール・ファクタ（イン）を精密に調整することによって、ゼロにすることができます。4 つの誤差をゼロに調整した後に残る誤差は、乗算器 の本質的な非線形性f（X,Y）によるものです。一般に非線形性を軽減することはできませんが、特定のケースでは、次の「トランスコンダクタンス乗算器」のセクションで説明されているように、かなりの部分を相殺することができます。

非線形回路ハンドブックの目次へ戻る