Combining the Best of Both Worlds: True Time Delays and Phase Shifters
Combining the Best of Both Worlds: True Time Delays and Phase Shifters
Jun 16 2022
Abstract
This article reviews the strengths and weaknesses of two electronic beamforming techniques: phase shifters (PSs) and true time delays (TTDs). It argues that these two methods can be combined in a hybrid beamforming architecture to offer better SWaP-C and a comparatively less complex system design.
Introduction
Electronically scanned arrays (ESAs) utilize PSs or TTDs or a mix of both to point the summed beam toward the desired direction within an array’s steering angle limits. Adjustable attenuators used for tapering can also be considered as beamforming elements. This article discusses where and how a tiered approach between TTDs and PSs in the same ESA can be helpful to mitigate some phased array design challenges.
Leveraging Fundamental Formulas to Explore Possible Scenarios
Instantaneous bandwidth (IBW) can be defined as the frequency band where no tuning is required to stay within the target performance criterion set by the system requirements.
TTDs exhibit constant phase slope over frequency; therefore, ESAs implemented with TTDs instead of PSs do not have beam squint effect. As a result, TTD-based ESAs are more convenient for high IBW applications.
PSs exhibit constant phase over their operating frequency range; hence, a particular phase shifter setting throughout the system results in different beam steering angles for different frequencies. As a result, PS-based arrays tend to have narrower IBW compared to TTD-based arrays.
This phenomena is called beam squint and it can be calculated using Equation 1 where Δθ is peak squint angle, θ0 is maximum beam angle, f0 is carrier frequency, and f is instantaneous signal frequency.

Using Equation 1, we can calculate that Δθ at worst case, that is at the low frequency edge (carrier at 3 GHz and instantaneous signal at 2.9 GHz), is around 1.15° for ±30° beam steering angle system for a signal at 3 GHz with 100 MHz IBW. Changing beam steering angle to ±60° and IBW to 200 MHz results in around 8.11° beam squint at worst case. It is evident that TTDs can be a better choice even in radar applications. Arguably, phase shifter dominance in ESAs can be explained by the fact that PSs have had wider market availability due to their design simplicity and cost advantage over TTDs.
If we had a TTD that meets the system requirements, how could it be reasonable to use PSs in the same signal chain?
To investigate, a 32 × 32 square ESA with d = λ/2 lattice spacing (d) between antenna elements desired to operate between 8 GHz and 12 GHz with ±60° scanning angle will be examined and EIRP criteria is assumed to be met for all scenarios (Figure 4).
In this example, the system beamwidth in both azimuth and elevation would be ≅ 3.17° at boresight (θ = 0°) and ≅ 6.35° at the max scan angle (θ = 60°) by the half power beamwidth approximation formula for a uniform linear array given in Equation 2 where N is the number of elements on one axis and θB is the beamwidth in degrees on the same axis.

The maximum beam angle resolution θRES_MAX of this array in one dimension when 6-bit 5.6° LSB PSs are used behind every antenna element would be approximately ≅ 0.056° by Equation 3.

Approximately 1.3 ps LSB TTDs would be required to replace 5.6° LSB PSs to have a 0.056° beam angular resolution at 12 GHz by Equation 4 that is used for conversion between time and phase shift.

The beamwidth value is considerably greater than the beam angular resolution even at very small scan angles and placing PSs on the same line with TTDs to compensate for beam angular resolution would introduce additional beam squint and beam angular resolution degradation into the system. In practice, the reason to have finer TTD resolution is to have lower quantization sidelobe levels (QSLL) rather than having finer beam angular resolution. As the frequency goes higher, designing a TTD with a required time resolution to meet the target QSLL criteria gets relatively more difficult than designing a PS with a required phase resolution; hence, PSs can be a companion of TTDs to achieve the target QSLL while still having an acceptable level of beam squint
Another reason to implement PSs and TTDs in the same ESA could be to mitigate beam squint while designing a system with cross polarization capability. Cross polarization is generated by setting a 90° phase shift in between the V and H feeds of antenna elements. Ensuring as close to a 90° difference as possible between feeds over the desired cross polarization bandwidth is essential to have good cross polarization isolation for a healthy operation. Due to the fact that having a constant phase over frequency, PS-based ESAs have a wideband cross polarization capability (Figure 1), unlike TTD-based ESAs that can have 90° between feeds only at a single frequency (Figure 2). The architecture in Figure 3 can be used for applying cross polarization while mitigating beam squint.
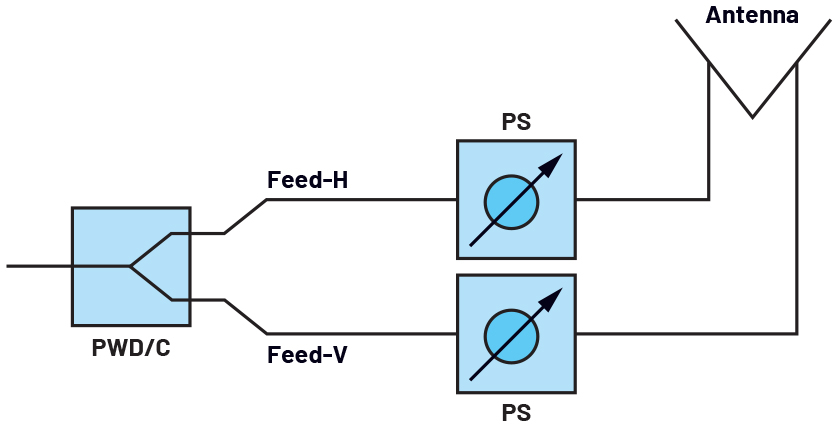
Figure 1. Nonsquint free wideband cross polarization with phase shifters behind the V and H feeds of antenna elements.
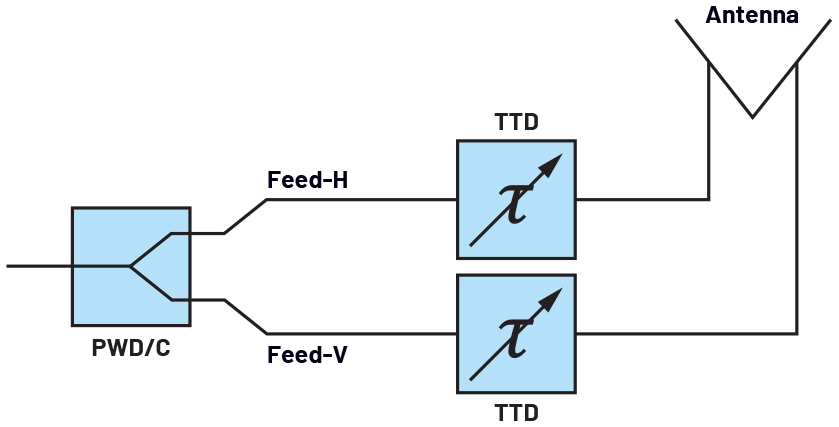
Figure 2. Squint free narrow-band cross polarization with true time delays behind the V and H feeds of antenna elements.
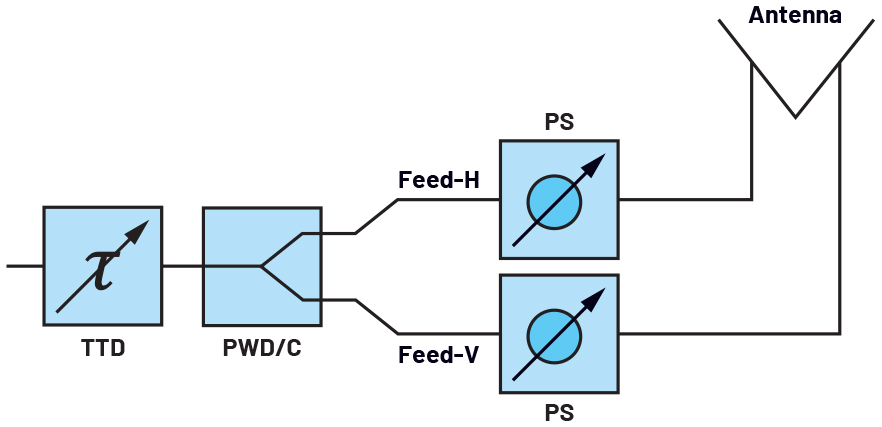
Figure 3. A true time delay on common leg and phase shifters behind the V and H feeds of antenna elements to optimize beam squint while having wideband cross polarization capability.
TTD coverage is set by the maximum delay ΔtMAX between most distant elements of the whole array at the lowest operation frequency. By Equation 5, this is around 2.45 ns for the example array in Figure 4.

There are a couple of things to consider when one thinks of using TTDs behind every antenna element instead of PSs when cross polarization is not required. This coverage means a significantly high loss and could be challenging to implement to fit into antenna spacing. Having a 6-bit phase PS’s resolution with the given coverage would bring some design challenges along with many delay stages to be placed into TTD.
If the resolution is preserved and the coverage is reduced to mitigate these drawbacks, then one would have to wrap back through zero when the coverage is exceeded (by calculating phase equivalent by Equation 4) but then the beam squint feature would ironically be lost.
This quick analysis shows that PSs at every antenna element followed by TTDs at the common legs of the subarrays can be useful even when cross polarization is not required. TTDs in Figure 4 would again need to have the same coverage, but this time the resolution requirement is relaxed compared to that of TTD at every antenna element case as now they are used to align relatively larger time delays between subarrays.
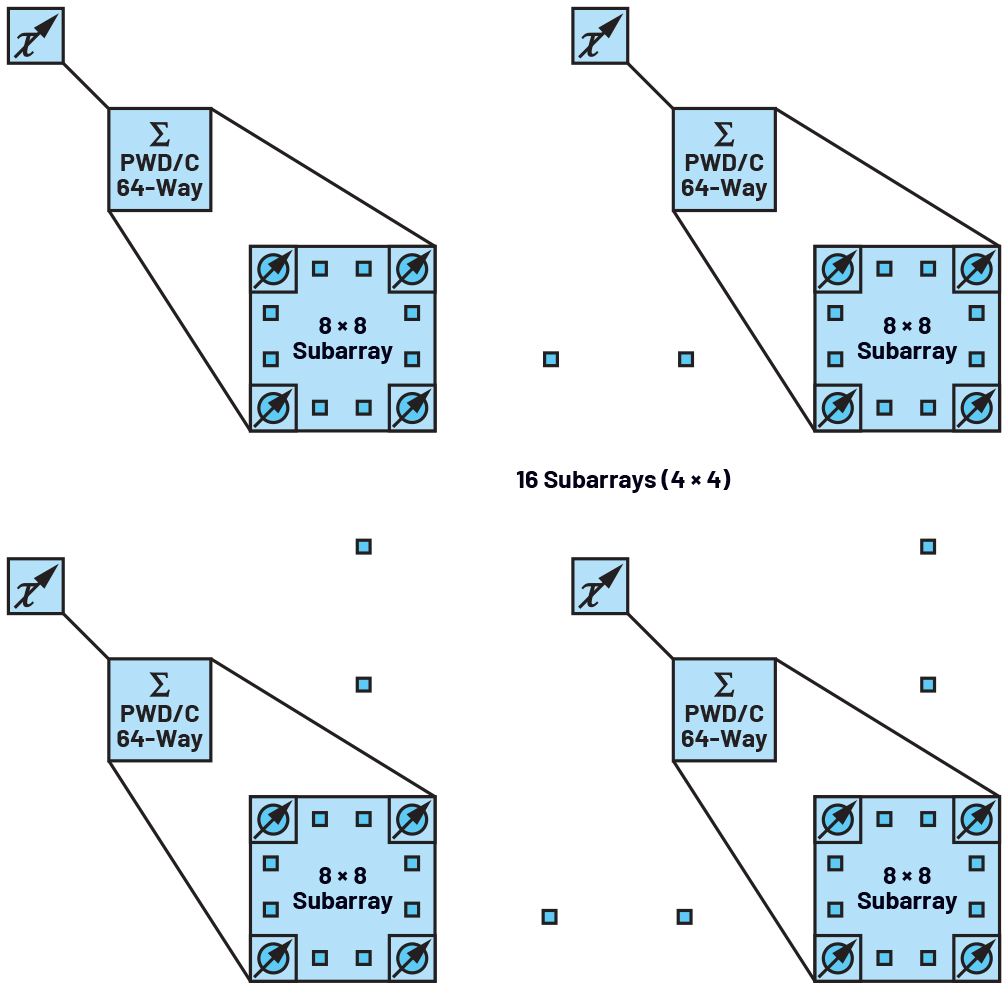
Figure 4. 1024 (32 × 32) element array partitioned into 16 subarrays consisting of 8 × 8 elements.
Breaking down a phased array into subarray partitions reduces the cost and complexity of a system at the expense of a higher scan loss and lower beam steering resolution. By having wider beamwidth, subarrays are more tolerant to beam squint effects as they have wider beamwidth. It is apparent that beam squint and beamwidth targets are important metrics with consideration to the subarray size.
Conclusion
True time delays behind every antenna element are required for a broadband squint free operation and phase shifters behind every V and H feed of each antenna element are required for a broadband cross polarization operation.
If cross polarization is not required and fully squint free operation is targeted, then TTD-based design should be followed. As the frequency increases, adding PSs could help to meet the QSLL target in return for a compromised squint free operation.
If cross polarization is required, then each polarization feed of the antenna should be followed by separate but identical PSs with a tight 90° difference above the operational bandwidth. Adding TTDs on the common leg of PSs could help to mitigate the beam squint.
Whether cross polarization is required or not, a subarray architecture with PSs behind antenna elements followed by TTDs at the common legs of subarrays can be a cost-effective solution. Note that TTD functionality can be implemented in a digital domain and all digital design can eliminate both TTDs and PSs at the expense of a higher system cost.
Before diving into the countless challenges of ESA design, understanding the differences in using either TTDs or PSs vs. using them in tandem is an essential part of planning a system level beamforming architecture that meets the system requirements with a better SWaP-C.
Analog Devices has a huge portfolio of solutions, platforms, and products for all analog, digital, and hybrid beamforming ESAs in a wide range of applications along with the capability to provide tailored power solutions for the complete signal chain.
About the Authors
Bilgin Kiziltas joined Analog Devices as a field applications engineer in 2019. He received his B.S. degree in electronics engineering from Istanbul Technical University in 2010 and his M.S. degree in RF, microwave, radar,...




