Abstract
Numerous factors affect random timing jitter, including noise sources such as phase noise, broadband noise, and spurs, as well as slew rate and bandwidth. This article explores these sources, and also provides equations to translate noise into timing jitter.
Introduction
Timing jitter and noise are among the least understood engineering concepts, yet they are among the most critical parameters in analog and digital designs. Especially true in high-speed communication systems, poor jitter performance can cause increased bit-error rates and limit system speed. Timing jitter is generally defined as the short-term variation of a significant instant of a digital signal from its ideal position in time. There are a number of factors that contribute to random timing jitter, including broadband noise, phase noise, spurs, slew rate, and bandwidth. Both phase and broadband noise are random, whereas spurs are deterministic responses caused by various identifiable interference signals, such as crosstalk and power supply coupling. As shown later in this article, slew rate and bandwidth also affect jitter. Figure 1 illustrates a non-ideal sinusoid that contains the three noise sources. Figure 2 shows a digital signal with jitter that accumulates over time.
The purpose of this article is to both explain and demonstrate the direct relationship between timing jitter and these three noise sources.

Broadband Noise Contribution to Timing Jitter
Jitter in Sinusoids
All electronic components, especially amplifiers and logic devices, generate broadband noise. Also known as the noise floor, broadband noise is a combination of shot noise and thermal noise. Commonly found in diodes and transistors, shot noise is caused by random hopping of charges across a potential barrier within a semiconductor junction. Thermal noise, on the other hand, is unaffected by current flow. It is caused by the random thermal motion of carriers, within a MOSFET's gate and channel resistance, for example. The thermal noise power is directly proportional to the resistance and temperature.
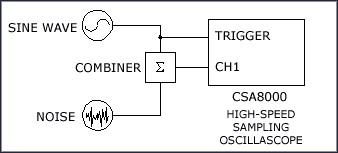
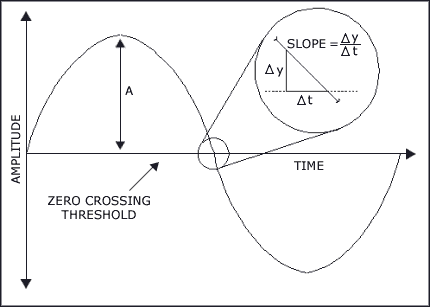
The effect of broadband noise on timing jitter becomes significant as the operating bandwidth of modern components pushes into the multi-GHz range. For example, a broadband amplifier driver with a 40GHz bandwidth, a 10dB noise figure, a 20dB small-signal gain, and an output power of 0dBm, generates a -38dBm noise output (-174dBm + 10dB + 20dB + 10log10(40GHz)). This results in a signal-to-noise ratio (SNR) of 38dB. At this SNR level, the broadband noise is a significant contributor to timing jitter. The total root-mean-square (RMS) noise voltage is the integral of the noise floor over the bandwidth. Figure 3 illustrates how RMS noise is translated into timing jitter.
Mathematically, you can represent a sinusoid containing broadband white noise with the following equation:

where A is the amplitude, ω is the angular frequency, and vn(t) is the noise voltage at time t. The random noise vn(t) has a Gaussian (normal) distribution. The probability distribution ƒ(vn) of the noise voltage (vn) is:

where (vnRMS) is the RMS noise voltage. To understand how noise voltage is translated into timing jitter, consider applying y(t) into the input of a jitter-measuring instrument, such as a sampling oscilloscope with a histogram function. Each time y(t) crosses the 0V threshold, a data point is added to the histogram. Just as depicted in Figure 3, at time Δt, there is a probability that the noisy signal Δy will reach the threshold; thus the jitter is added to the histogram at Δt sooner or later than the anticipated sampling point. The probability density as a function of the timing jitter Δt is calculated by setting vn = Δy = Asin(2πƒΔt) in Equation 2. The result is the jitter distribution function as shown in the histogram.
Equation 3 can be simplified by assuming that Δt is small when compared to the period of the sinusoid; therefore, Asin(2πƒΔt ≅ A(2πƒΔt = AωΔt.

Equation 3 then becomes:

Dividing the numerators and denominators of various terms within Equation 4 by Aω yields:

Equation 5 is a jitter distribution function similar to the Gaussian distribution shown in Equation 2, except for the scale factor 1/Aω. Thus, the RMS jitter is found as:

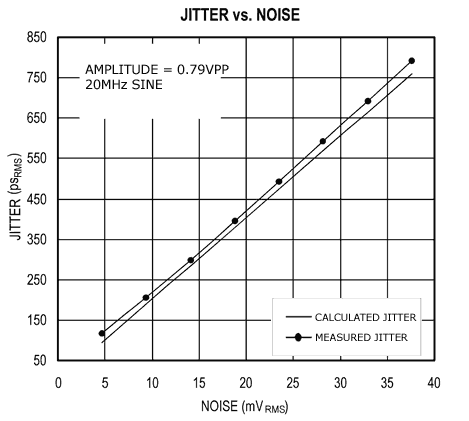
The test setup shown in Figure 4 was used to verify Equation 6. Both a clean sinusoid and a broadband noise signal were combined and input into a sampling oscilloscope, where jitter was measured at the zero crossing. To ensure meaningful results, the input broadband noise was set higher than the noise floor of the oscilloscope. Figures 5 and 6 show the results of the experiment. Figure 5 shows jitter as a function of frequency with constant RMS noise, while Figure 6 shows jitter as a function of RMS noise voltage with constant frequency. The similarity between the measured and calculated jitter curves proves that Equation 6 can be used to translate broadband noise into timing jitter.
Jitter in General Waveforms
With slight modification, Equation 6 can also accommodate the jitter translation of other waveforms. By definition, the Aω term shown in Equation 6 is the slew rate S at the 0V threshold. Any waveforms with a known slew rate at the threshold can be used to relate Δt to Δy, because vn = Δy = SΔt (Figure 3). Substituting this into Equation 2 yields Equation 7.

Dividing the numerators and denominators of various terms within Equation 7 by S yields:

Equation 8 is similar to the Gaussian distribution shown in Equation 2, except for the scale factor of 1/S. Thus, the RMS jitter is:

The test setup shown in Figure 4 was again used to verify Equation 9. The sinusoid was replaced by a variable-slew-rate square wave. Jitter was measured at the 50% point of the rising edge of the square wave. The results shown in Figure 7 illustrate the validity of Equation 9.
The information presented in Figure 7 raises an interesting point. It appears that a faster slew-rate waveform results in lower jitter. However, a faster slew rate requires a higher operating bandwidth, which increases the RMS noise of the system. Because the RMS noise is directly proportional to the bandwidth, system designers must carefully choose the slew rate and bandwidth to minimize jitter.
Phase Noise Contribution to Timing Jitter
Phase noise is present in every active and resistive component, but it is most severe in oscillators. These oscillators include free-running crystal oscillators and phase-locked oscillators in clock recovery applications. Phase noise is a specification that characterizes spectral purity. For example, an oscillator output should ideally be a pure sinusoid represented as a vertical line stationed on a single frequency in the frequency domain. However, in reality, there are noise sources in the oscillator that can cause the output frequency to deviate from its ideal position, thus generating a "skirt" of other frequencies near the carrier (fundamental) frequency (Figure 8). Referred to as phase noise, these frequencies result from the noise sources modulating the oscillator. They often appear above the noise floor and close to the carrier frequency. Phase noise is usually specified as the ratio of a noise power at an offset frequency away from the carrier to the carrier power, in a 1Hz bandwidth. Because the noise source's frequency modulates the signal to produce phase noise, phase noise is unaffected by the slew rate.
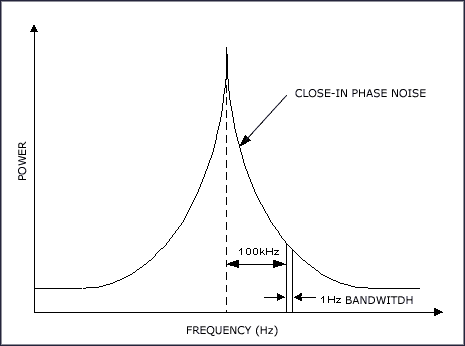
Due to the limitations of most jitter-measuring equipment, it is often easier to characterize the purity of a low-noise signal by measuring its phase noise in the frequency domain, rather than measuring jitter in the time domain. For example, most jitter-measuring oscilloscopes are only capable of measuring jitters down to 1psRMS. Most modern real-time oscilloscopes only have bandwidths up to 7GHz. Phase-noise equipment, on the other hand, can measure noise levels of the best low-noise oscillators available (much less than 1ps in time domain) and offer bandwidths of up to 40GHz.
The translation between phase noise and timing jitter has been explored in previous articles [1-2]. To derive the necessary equations relating phase noise to jitter, consider Equation 10 as a sinusoid containing phase noise:

where A is the amplitude, fo is the nominal frequency, and Φ(t) is the phase noise. Jitter is commonly measured at the 0V crossing between two or more periods. At the 0V crossing, the terms inside the parentheses of Equation 10 is 2πN:


where t1 is the first zero-crossing and t2 is the Nth zero-crossing. Subtracting the two equations yields:

The time between the two zero-crossings is the number of periods plus the jitter:

TO is the period or 1/fO, and Δt is the jitter accumulated after N periods. Substituting Equation 14 into Equation 13 yields:

Rearranging Equation 15 and cancelling out the 2πN terms yields the jitter:

The squared RMS jitter is:

Because Φ(t) is a stationary process:

where SΦ(ƒ) is the spectral density of Φ(t), and f is the offset (Fourier) frequency. The middle term of Equation 17 then becomes:

where RΦ(τ) is the autocorrelation function of Φ(ƒ), and τ ≅ NTo is the time after the Nth period. The squared RMS jitter after the Nth period at time τ is:

Recalling the algebraic identity 1 - cos(2Φƒτ = 2sin²(Φƒτ) and assuming the phase noise is close to the carrier and symmetrical (meaning the integration from -fOFFSET to 0 equals to the integration from 0 to +fOFFSET), Equation 20 can be rewritten as:

SΦ(ƒ) is approximately equal to the phase noise L(ƒ) for close-in phase noise [3]; that is, the Fourier offset frequency is much less than the carrier frequency: fOFFSET << fO.

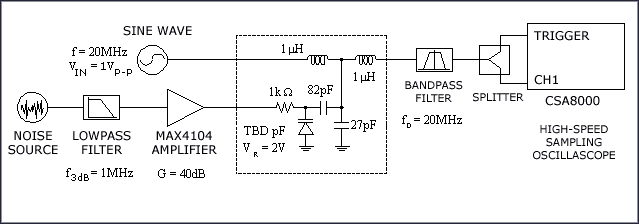
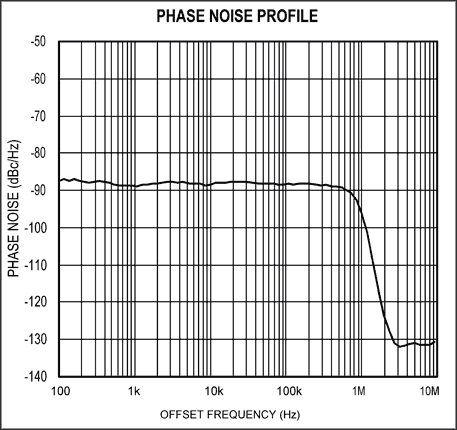
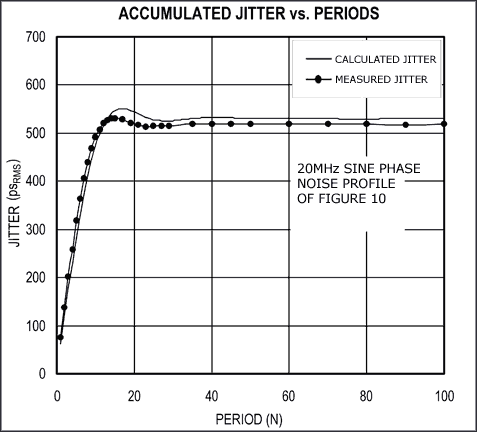
A phase-modulating circuit [4] was used as part of the test setup shown in Figure 9 to verify Equation 22. The phase-modulating circuit provides a convenient way to produce a variable phase-noise signal that is free of spurs. The output of the circuit was first measured for timing jitter with a sampling oscilloscope, then measured for phase noise with a spectrum analyzer (not shown). Figure 10 shows the phase noise profile of the circuit. It is similar to the noise profile of a phase-locked oscillator, where the phase noise is constant inside the loop bandwidth and rolls off outside the bandwidth. Using numerical integration to integrate Equation 22, the resulting accumulated jitter with respect to period was plotted in Figure 11. The curves shown in Figure 11 confirm the validity of Equation 22.
Spurious Noise Contribution to Timing Jitter
Spurs also contribute to timing jitter, especially in oscillators. Spurs are caused by phase-locked-loop reference spurs, supply coupling, crosstalk from nearby circuitry, and sources. As shown in Figure 1, these spurs usually appear as small spikes near the carrier frequency. Equation 22 can help relate spurs to timing jitter. Because spurs only occur at specific frequencies, the integration function in Equation 22 can be replaced with a summation:

Again, τ ≅ NTo is the time after the Nth period. Since Equation 23 does not assume that the spurs are symmetrical, it is multiplied by a factor of 4 instead of 8. The spurs on both sides of the carrier must be included in the jitter calculation. L(fn) is the spur amplitude relative to the carrier (the desired signal) and is usually given in dBc. fn is the offset frequency of the nth spur. Figure 12 shows the plot of Equation 23 using a spur on both sides of the carrier at an offset of 100kHz offset and an amplitude of -40dBc. Reference 1 verifies Equation 23 by modulating a voltage-controlled crystal oscillator with a sinusoid to produce a spur on each side of the carrier (not shown).
Total Jitter
As previously mentioned, broadband noise, phase noise, and spurs are the three contributors to timing jitter. Broadband noise is purely random and uncorrelated, thus the jitter it produces does not accumulate. The latter two, however, generally do produce accumulating jitter. The squared total timing jitter is the sum of the three squared jitters.

Conclusion
The correlation between the experimental and calculated data demonstrates the relationship between the three major noise sources and timing jitter. Designers of high-speed systems can use equations 9, 22, and 23 to translate noise into timing jitter.
Side-Bar: Calculate RMS Noise Voltage
There are several ways to determine the total RMS noise voltage of an electronic device if you know one or more of its conventional noise specifications. Table 1 shows a list of noise specifications that component manufacturers usually provide.
| Component | Noise Specification | Unit |
| Amplifier | Residual noise-floor power density | dBm/Hz |
| Noise figure | dB | |
| Input referred noise density | ||
| Oscillator | Phase noise floor | dBc/Hz |
If the noise density is given, you can estimate the total RMS noise by integrating the noise density over the effective bandwidth, as shown in the following equations:

The system load impedance ZO is typically 50Ω. PRMS is the RMS noise power, BW is the bandwidth, and NOISE-FLOOR is the noise floor density in dBm/Hz. For example, an amplifier with an output noise density of -150dBm/Hz and a 10GHz bandwidth generates a total RMS noise voltage of 707µVRMS:

Noise figure (NF) is often used to characterize the noise performance of low-noise amplifiers and power amplifiers. You can derive the noise-floor density from the noise figure by summing it with the thermal noise of a 50Ω resistor and the system gain, as shown in the following equation:

For example, an amplifier with a 10dB noise figure, and a 20dB small-signal gain, has a noise floor density of -144dBm/Hz:

Knowing the noise density allows the derivation of the total noise voltage.
Op amp noise performance, on the other hand, is usually given in the form of input referred noise in . Assuming the noise current is negligible and the source impedance is much smaller than the amplifier's input impedance, the total RMS noise can be calculated with the following equation:

For example, an op amp with an input-referred noise density of 8nV/√Hz, a small-signal gain of 20dB, and a bandwidth of 1GHz, generates 800µVRMS of noise voltage:

The phase noise of oscillators is usually given in dBc/Hz. The unit dBc indicates the normalization of the output noise to the desired signal power. The following equation can be used to obtain the total RMS noise voltage:

where PSIG is the oscillator output power. For example, an oscillator with an output power of 10dBm into 50Ω, an output phase noise floor of -150dBc/Hz, and an effective bandwidth of 100MHz, the output noise voltage is 224mVRMS: