A Quantitative Analysis of the Power Advantage of Hybrid Beamforming for Multibeam Phased Array Receivers
A Quantitative Analysis of the Power Advantage of Hybrid Beamforming for Multibeam Phased Array Receivers
by
Prabir Saha
Dec 1 2021
Abstract
In this article, a comparison focused on the power efficiency of analog, digital, and hybrid beamforming architectures is presented. A detailed equation-based model for the power consumption of the three architectures was developed for a receive phased array. The model clearly illustrates the contributions of various components to the total power consumption and how the power scales with various array parameters. A comparison of power consumption per beambandwidth product for the different array architectures shows the advantage of the hybrid approach for millimeter wave phased arrays with a large number of elements.
Introduction
In this article, the different methods of beamforming are compared, specifically focusing on the ability to create multiple simultaneous beams and power efficiency. Phased arrays are playing an increasingly important role in modern radar and communication systems, and that brings renewed interest in improving system performance and efficiency. Digital beamforming (DBF) and its benefits as compared to the traditional analog approach have been well-known for many decades, but various challenges related to digital signal processing have held back its adoption. With the continuous shrinking of feature size and resulting exponential growth in computing abilities, we are now seeing widespread interest in the adoption of digital phased arrays. While DBF has many attractive properties, increased power consumption and cost remain a concern. A hybrid approach to beamforming may be suitable for many applications due to superior power efficiency.
Analog vs. Digital Beamforming
Beamforming, at its core, is a delay and sum operation, which can happen either in the analog or digital domain. Analog beamforming can again be classified into subcategories depending on where in the signal chain the delay or phase shift is being applied. In this article, only RF beamforming is considered. As shown in Figure 1a, the signals from the antenna elements are weighted and combined to create a beam before being processed by the mixer and the rest of the signal chain. This is how phased arrays have been implemented traditionally.
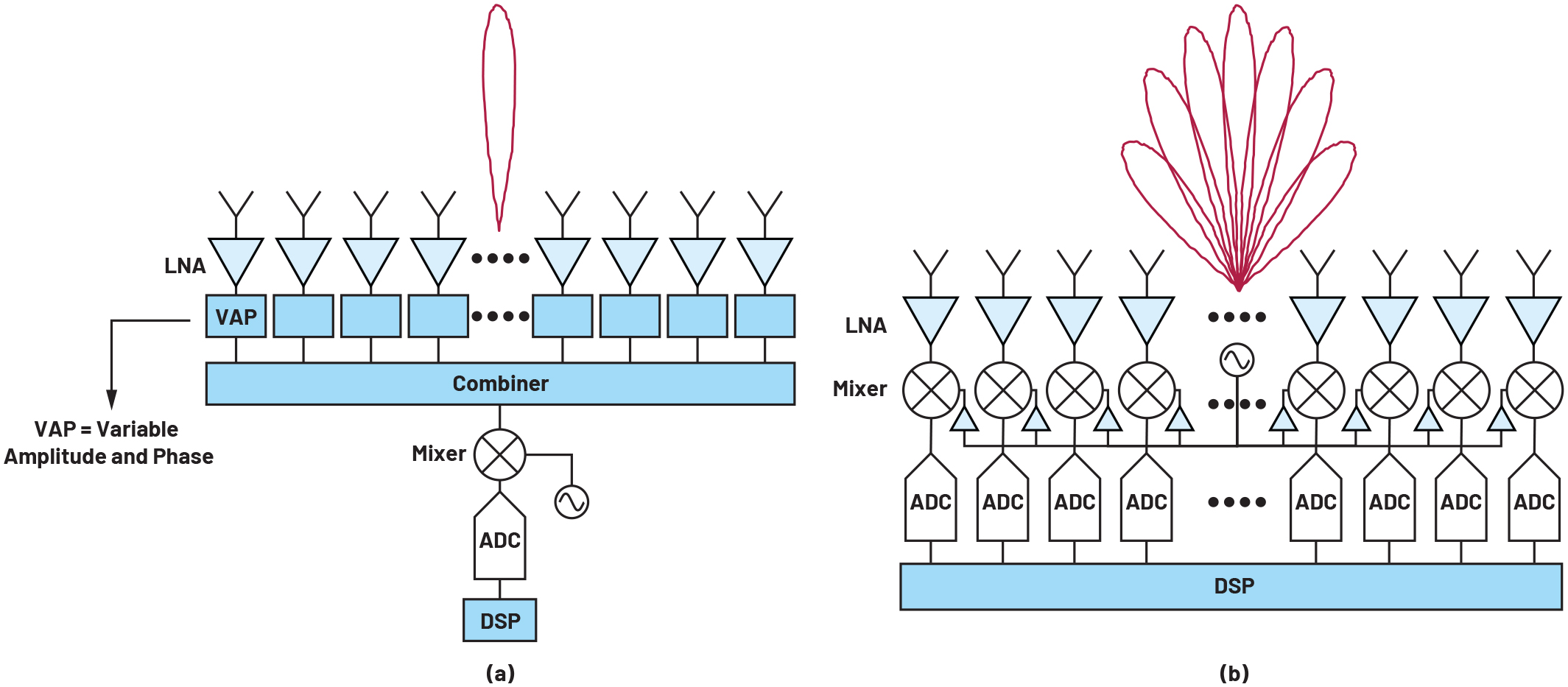
Figure 1. Comparison of (a) analog and (b) digital beamforming architectures.
One of the downsides of this architecture is the difficulty in creating a large number of simultaneous beams. Now, to create multiple beams, the signals at each element need to be split before being delayed and summed independently. The number of variable amplitude and phase (VAP) blocks needed to do that is proportional to the number of elements and the number of beams. The VAP blocks and the splitting and combining of networks take a lot of area, and, beyond a few beams, the increasing area requirements and complexity of the splitting and combining networks make it impractical to implement multiple simultaneous analog beams. For a planar array, the increasing area also makes it difficult to fit the electronics inside the grid determined by the element spacing. Also, more fundamentally, with each splitting, the signal-tonoise ratio (SNR) decreases, and the noise floor imposes a limitation on how many times the signal can be split before getting buried in the noise floor.
With DBF, on the other hand, it is relatively easy to create multiple simultaneous beams. As shown in Figure 1b, the signals for each element are digitized independently and then the beamforming operations take place in the digital domain. Once in the digital domain, a copy of the signals can be created without any loss in fidelity. The new copy of the signals can then be delayed and summed to create a new beam. This can be repeated as many times as necessary, giving rise to an infinite number of beams, in theory. In practice, the limits of digital signal processing and associated power and cost will limit the number of beams or the beam-bandwidth product. Moreover, the number of beams in DBF can be reconfigured on-the-fly, which is not possible with analog techniques. DBF also promises better calibration and adaptive nulling. All these advantages make DBF attractive for a variety of phased array applications in communication and radar systems. But all these benefits come at the expense of increased cost and power consumption. DBF at the baseband requires an ADC and a mixer for each element, as opposed to one for each beam for analog beamforming. The increased number of components increases power and cost significantly, especially for a large array. Also, since the beamforming in DBF happens at baseband, the mixers and the ADC are subjected to any signal present in the broad field of view of each element and thus are required to have enough dynamic range to be able to handle possible interferers. For beamforming at RF, the mixer and the ADC enjoy the benefit of spatial filtering and hence, the dynamic range requirement can be relaxed. The distribution of the high frequency LO signals while maintaining phase coherence is also a challenge for DBF implementation and adds to the power consumption.
The computational requirement of digital beamforming is a significant contributor to the overall power consumption. The amount of data the DSP must process is proportional to the number of elements, number of beams, and instantaneous bandwidth of the signal.

For a large array operating at millimeter wave frequencies, where the signal bandwidth is typically large, the data load can be astronomically high. For example, for a 1024-element array, with 500 MHz bandwidth and 8-bit ADC, the DSP needs to process about 8 Tb of data per second per beam. Moving and processing this large amount of data requires a significant amount of power. In terms of computational load, this would translate to about 4×1012 multiplication operations per second for each beam. For multiple beams at full signal bandwidth, the necessary computational power is beyond the reach of today’s DSP hardware. In a typical implementation, the beam-bandwidth product is held constant so that for the increasing number of beams, the total bandwidth is divided among the beams. The digital signal processing is often done in a distributed fashion to be able to cope with the huge amount of data. But that usually entails various tradeoffs among beamforming flexibility, power consumption, latency, etc. In addition to the processing power, a significant amount of power is also consumed by the high speed input/output data interfaces of the various DSP blocks.
Hybrid Beamforming
Hybrid beamforming, as the name suggests, combines analog and digital beamforming techniques to provide a middle ground between the two. One way of doing this is to divide the array in smaller subarrays and perform analog beamforming within the subarrays. If the number of elements in the subarray is relatively small, the resulting beam is relatively broad, as illustrated in Figure 2. Each subarray can be thought of as a super-element with a somewhat directional radiation pattern. Digital beamforming is then performed using the signals from the subarrays, which produces high gain, narrow beams corresponding to the full aperture of the array. Using this approach, the number of mixers and ADCs, as well as the size of the data processing load, decrease by the size of the subarray compared to full digital beamforming. This results in significant savings in cost and power consumption. For a 32×32 element array, a subarray size of 2×2 results in 256 subarrays with a half power beamwidth (HPBW) of 50.8° or 0.61 steradians. Using the signals from the 256 subarrays, as many beams as practical can be created using DBF. The HPBW corresponding to the full aperture is 3.2° or 0.0024 sr. Roughly 254 digital beams can then be created within the beam of each subarray without significant overlap with each other. One limitation of this approach compared to full DBF is the fact that all the digital beams will be contained within the field of view of the subarray pattern. The subarray analog beam can of course be steered as well, but at one single point of time, the analog beamwidth imposes a restriction on where the final beam can be directed.
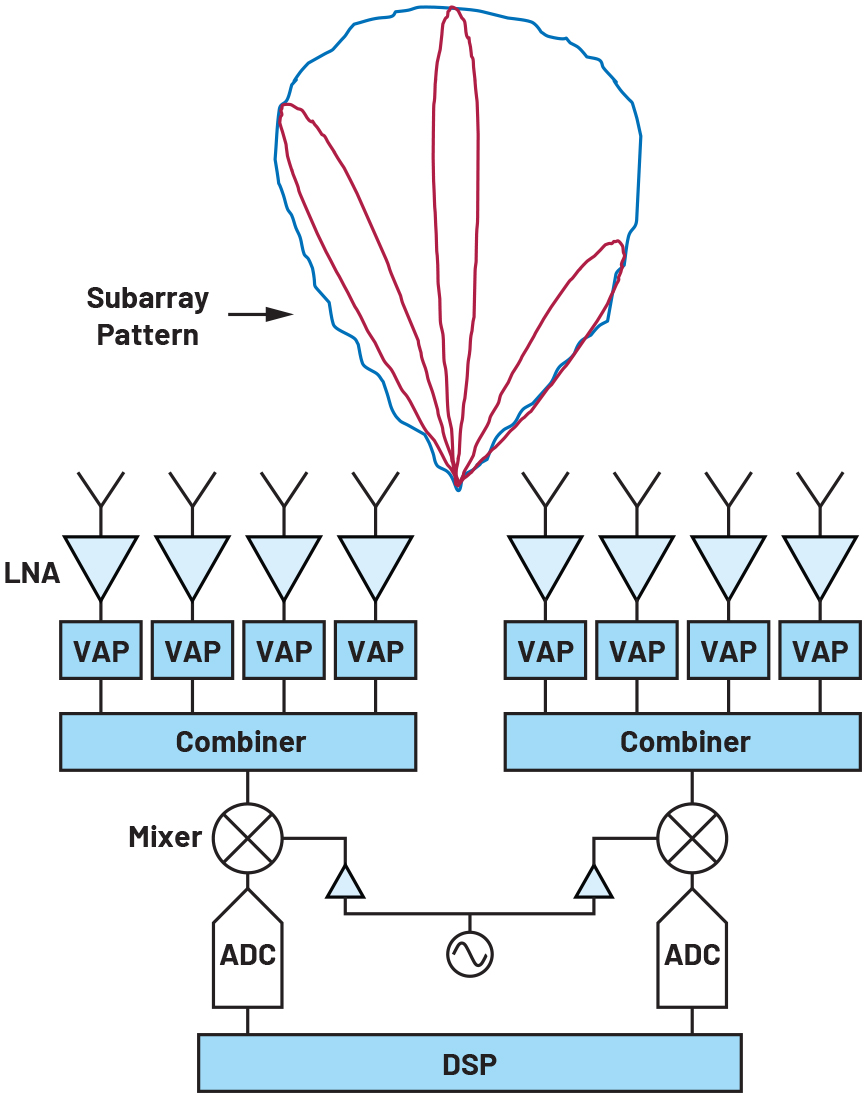
Figure 2. Hybrid beamforming.
Since the subarray pattern is typically broad, this may be an acceptable trade-off for many applications. For others requiring more flexibility, multiple independent analog beams can be created to address this issue. This will require additional VAP blocks at the RF front end, but still can reduce the number of ADCs and mixers compared to full DBF. As illustrated in Figure 3, two analog beams can be created for greater coverage while still cutting down on the number of mixers, ADCs, and the resulting data streams by a factor of two.

Figure 3. Hybrid beamforming with multiple analog beams.
Hybrid beamforming also results in degraded side lobes compared to DBF. When the digital beams are scanned away from the center of the analog beam, phase errors are introduced because of the hybrid nature of phase control. The phase delta between the elements within a subarray is determined by the analog beam control and remains fixed irrespective of the digital scan angle. For a given scan angle, the digital control can apply the proper phases only to the center of the subarrays, and the phase errors increase as we move away from the center toward the edge of the subarrays. This results in a periodic phase error across the entire array, reducing the gain of the beam and producing quasi side lobes and grating lobes. These effects increase with increasing scan angle, and this is one downside of hybrid beamforming compared to pure analog or digital architectures. The degradation in side lobes and grating lobes can be improved by making the errors aperiodic, which can be achieved by mixing subarray sizes, orientations, and locations.
Power Efficiency
In this section, the power efficiency of analog, digital, and hybrid beamforming are compared from the perspective of a receive phased array. The models for power consumption of analog, digital, and hybrid beamforming are given in equations 2, 3, and 4, respectively. The meaning of the various symbols and their assumed values for the subsequent analysis are given in Table 1.



| Symbol | Meaning | Value | Ref |
| PLNA |
LNA power consumption |
15 mW/instance |
1 |
| Plosscomp |
Power to compensate for various losses in RF/LO paths |
1.5 mW/dB | 1 |
| Pmixer |
Mixer/LO amplifier power consumption |
40 mW/instance | 2 |
| PADC |
ADC power consumption; 8-bit, 1 GSPS |
5 mW/instance | 3, 4 |
| b |
Number of ADC bits | 8 | |
| PDSP-comp |
DSP power for beamforming computation |
1.25 mW/GMAC | 5 |
| PSerdes | DSP power for I/Os |
10 mW/Gbps | 6 |
| LVAP |
Loss due to passive gain and phase control | 10 dB | 7 |
| Lsplit |
Loss of the power splitter for ABF | 4 dB | |
| Lcomb |
Loss in the power combiner for ABF |
1 dB |
|
| Lpath |
RF/LO routing loss per unit length | 0.05 dB/mm | 8 |
| D | Length/width of the array | 155 mm | |
| Ds |
Length/width of the subarray |
15 mm | |
| Dx |
Additional length factor for routing and combining RF signals | 0.25 | |
| m | Number of elements |
1024 | |
| ms |
Number of elements in the subarray | 16 | |
| n |
Number of beams |
— |
|
| ns |
Number of analog beams in hybrid beamforming |
4 | |
| IBW |
Instantaneous bandwidth of the signal | 500 MHz | |
| DSPTP |
Maximum throughput of the DSP for DBF | 8 TSPS |
Some key points regarding the power consumption model are:
- The RF signal power at the mixer is assumed to be the same for all three beamforming architectures.
- In some published literature, it has been argued that for DBF, since the effect of the quantization noise of the ADCs on the SNR is reduced by the array factor, the required number of bits can be reduced as compared to analog beamforming. However, in DBF the ADCs also need to have higher dynamic range because they do not enjoy the benefits of spatial filtering and need to handle all the interferers present in the field of view of each element’s radiation pattern. Considering that, the number of bits of the ADC are assumed to be the same for all the cases in this model.
- For DBF, the beam-bandwidth product is limited by the processing capacity of the DSP, which is taken into account by the variable DSPTP. For the hybrid case, the maximum processing capacity was reduced in proportion with the reduction in power consumption.
- The DSP power for DBF has two components—computation and I/O. Each complex multiplication requires four real multiply and accumulate (MAC) operations and based on “Assessing Trends in Performance per Watt for Signal Processing Applications,”5the power consumption for the MAC operations was calculated to be around 1.25 mW per GMAC. The I/Os consume the bulk of the DSP power in this case, and it was estimated to be 10 mW/Gbps based on “A 56-Gb/s PAM4 Wireline Transceiver Using a 32-Way Time-Interleaved SAR ADC in 16-nm FinFET.” 6 For more complex beamforming approaches requiring more intensive computation, the power ratio will be less skewed, but the total DSP power will increase. Also, the I/O power consumption in this model assumes the bare minimum data transfer. Depending on the DBF architecture, the power consumption in the I/Os can be higher.
- The power for the ADCs and DSP computations depends exponentially on the number of bits. So, those power numbers can be reduced substantially by reducing the number of bits. On the other hand, the DSP I/O power, which is the biggest contributor, scales less drastically with the number of bits.
- The routing loss (Lpath) was calculated by combining losses of GCPW transmission lines on silicon ICs and low-loss PCBs. For on-chip transmission lines, the loss was assumed to be 0.4 dB/mm and for the PCB traces,8 the loss was taken as 0.025 dB/mm. It was also estimated that 5% of the lines will be on chip and the rest will be on the PCB. For analog beamforming, the routing loss necessary for RF combining was taken into account, while for digital beamforming, the loss of the LO distribution network was included.
- For the hybrid model, it is assumed that each beam corresponds to the full aperture of the array.
The dependence of power consumption on the number of beams is shown in Figure 4. For the analog case, varying the number of beams requires a design change, while in DBF the number of beams can be changed on-the-fly with the same design. For the hybrid case, a single design with a fixed number of analog beams (ns) is considered. It is also assumed that, when the number of beams is less than ns, the amplifiers in the unused paths are powered down.

Figure 4. Power consumption vs. number of beams for analog, digital, and hybrid (with four analog beams) beamforming architectures. For the analog case, the line is shown as dotted beyond four beams to represent the difficulty of implementing more beams using analog techniques. For the digital and hybrid cases, the power and the beam-bandwidth product becomes constant once the capacity of the DSP is reached.
For a single beam, the digital implementation consumes a lot more power because of the overhead of additional mixers, LO amplifiers, and ADCs. The rate at which the power increases is dependent on the increased aggregate data rate for the digital case; and for the analog case, it is related to the power required to compensate for losses from splitting and additional VAP blocks. Because of the aforementioned complexities of splitting and combining networks, it is impractical to implement a large number of beams using analog beamforming and the dotted line for more than four beams reflects that fact. For DBF, once the maximum DSP capacity is reached, the power consumption does not increase anymore. Beyond that point, bandwidth per beam is reduced for an increasing number of beams. DBF does break even with ABF in terms of power consumption and consumes less power for a large number of beams. The hybrid approach reduces the power overhead and the slope significantly compared to DBF and achieves the break-even point much sooner.
The power efficiency of beam formation for the three cases is compared in Figure 5, in which the power consumption per beam-bandwidth product is plotted. In this case, analog beamforming remains more efficient throughout. The hybrid approach starts somewhere in between the two extremes and becomes comparable to the analog case for a larger number of beams.

Figure 5. Comparing power efficiency of analog, digital, and hybrid beamforming architectures.
Conclusion
The comparisons and the power consumption models presented in this article are applicable only for a receive (Rx) phased array. For the transmit case, some of the underlying assumptions will change and the power penalty for a full DBF architecture is likely to be less severe. Even for the receive case, the difference between the three architectures is heavily dependent on the parameters outlined in equations 2 through 4. For parameter values other than those given in Table 1, the difference between the graphs will change. But it can be safely said that a hybrid approach will provide significant power savings for many applications while retaining most of the benefits of digital beamforming. As mentioned earlier there are downsides of going the hybrid route, but those trade-offs are likely to be worth the power savings for many applications.
About the Authors
Prabir K. Saha received a Ph.D. degree in electrical engineering from Georgia Institute of Technology, Atlanta, GA, USA in 2013. His research interests include design of RF/microwave, analog, and digitally assisted adaptiv...
Related to this Article
Products
RECOMMENDED FOR NEW DESIGNS
17 GHz to 22 GHz, 4-Beam and 4-Element, Ka-Band Beamformer
RECOMMENDED FOR NEW DESIGNS
27.5 GHz to 31 GHz, 4-Beam and 4-Element, Ka-Band Beamformer




















