Abstract
The 3GPP UE spec for TD-SCDMA states that the unmodulated frequency error between the UE and the BS must not exceed ±0.1ppm. A real-world interpretation of this spec is provided. Recognizing that the only contributing factors for the UE are system AWGN and Tx/Rx phase noise, a statistical analysis based on superposition of these two factors is provided to set a limit on UE transceiver phase noise. It is shown that the Maxim TD-SCDMA v2.0 Reference Design meets this phase noise spec with margin.
Scope
According to TD-SCDMA standard, one specification is that the UE modulated carrier frequency shall be accurate to within ±0.1ppm observed over a period of one timeslot compared to carrier frequency received from the BS. This article will detail the factors that affect this specification. Through simulation, we know how much the added white noise affects this specification, therefore then we can deduce the minimum requirements for the handset/user equipment (UE) Rx and Tx PLL phase noise.
The Standard for TD-SCDMA UE
About UE frequency stability specification, 3GPP TS 34.122 V4.7.0 gives below description:
Definition and Applicability
The frequency stability is the difference of the modulated carrier frequency between the RF transmission from the UE and the RF transmission from the BS. The UE shall use the same frequency source for both RF frequency generation and chip clocking.
Minimum Requirements
The UE frequency stability, observed over a period of one timeslot, shall be within ±0.1ppm compared to signals received from the BS.
Method of Test
1.28Mcps TDD Option
- Connect the SS to the UE antenna connector as shown in Figure 1.
- A call is set up according to the Generic call setup procedure using parameters as specified in Table 1.
- Enter the UE into loopback test mode and start the loopback test.
| Parameter | Value/Description |
| SS level (Ior) | -108dBm/1.28MHz (reference sensitivity) |
| UL reference measurement channel | 12.2kbps according to annex C.2.1.2 |
| Data content | real life (sufficient irregular) |
Procedure
- Measure the frequency error delta f across the TS according to annex B.
- Repeat step 1 for 200 bursts (time slots).
Test Requirements
For all measured bursts (time slots), the frequency error, derived in the Procedure clause, shall not exceed ±(0.1ppm + 10Hz).

Figure 1. Test Configuration.
How to Interpret the Standard
From the above description, we can see that it stresses two test conditions: 1) the signal power is -108dBm/1.28MHz (reference sensitivity power level); 2) test period is one time slot (675µS for TD-SCDMA). These two conditions will affect UE base band to estimate the receiving signal's carrier frequency. Only two factors in the UE radio affect this specification: the affects of added white Gaussian noise (AWGN), and the PLL phase noise. See Figure 2 below.
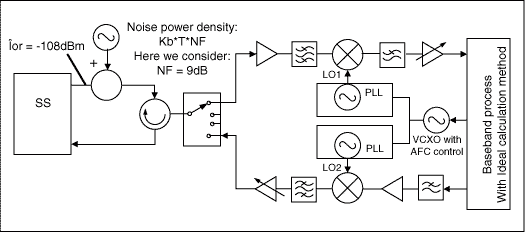
Figure 2. Analysis Model.
As we know, both the AWGN and LO phase noise are random processes, and they are not correlative. For easy analysis, we will solve this by superposition; we will calculate these affects separately, and add their affects at the end.
The Affects of AWGN
The AWGN will degrade the base band's ability to estimate carrier frequency, and results in an error of transmitted signal's carrier frequency. Here we assume that the estimate error is equal to the error of transmitted signal's frequency, and AWGN is a random process, the estimate error also follows a Gaussian distribution.
According to TR25.945's suggestion, here we take 9dB noise figure for receiving path, then the power density of the AWGN equal to kB*T*NF (noise figure taken as a linear ratio, not dB). We get the simulation result below:

Figure 3. The probability distribution of frequency estimate error.
Note that the red part of above picture is simulation result, and blue curve is normal distribution curve with
Through further simulation, we get the following:

Using this equation, we get σ = 45.6Hz, it's very close to the simulation result. Note Ps is equal to -108dBm, Ts = 675µS.
The Affects of Phase Noise
For this part of the analysis, we assume AWGN is equal to zero. We know the timed differential of phase noise is instantaneous frequency error, and the normal frequency error is the average value of this instant frequency error over a specified time period. When UE base band estimates the received signal's carrier frequency, this average frequency error will be equal to the estimated frequency error, and the transmitting path LO will result in additional frequency error, the total frequency error is then the sum of Rx and Tx average frequency error.
Assuming the phase noise is a smooth Gaussian procedure with µ = 0, power spectral density equal to GΘ(ƒ), then the instantaneous frequency is also a smooth Gaussian procedure with µ = 0, power spectral density equal to ƒ²GΘ(ƒ), the standard error of the average frequency error over one time slot is given by equation 2, the probability distribution is standard normal distribution.

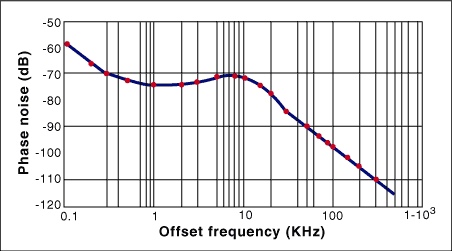
Figure 4. MAX2392 phase noise.
Above phase noise curve is the test result of Maxim TD-SCDMA v2.0 receive path. This reference design uses the MAX2392 zero-IF receive IC which integrates the PLL and VCO. Using this result, we get σƒTsRx = 16.5Hz. Note Ts = 675µS, and the integrated frequency range is 100Hz to 1MHz.
For Maxim TD-SCDMA v2.0 transmitting path, use same method, and get σƒTsTx = 9.6Hz, combine Tx and Rx, we get:

The UE Tx/Rx Requirement for LO Phase Noise
From the analysis above, we know that the frequency error is a random process; the probability distribution is standard normal distribution. The center frequency of the TD-SCDMA band is about 2GHz, and so a 0.1ppm frequency error is about 200Hz. Adding design margin, target a standard frequency error less than 200Hz/3.
Assuming the standard error from the added white noise is σn, the standard error from Tx and Rx Lo phase noise is σƒTs, then here has a limitation as below:

Considering σn = 46.7Hz, then we get the limitation of σƒTs:

Comparing equation 3 and 5, we see that the phase noise specification of Maxim TD-SCDMA v2.0 Reference Design meets out interpreted phase noise spen with margin.




















