Loop Gain and its Effect on Analog Control Systems
Abstract
This article brings together the ideas of open loop gain, closed loop gain, gain and phase margin, minimum gain stability and shows how these parameters are interrelated in a feedback system. It examines loop gain in terms of a theoretical control system as well as practical electronic circuits, including linear regulators.
Introduction
Bob Dobkin’s 2014 New Linear Regulators Solve Old Problems article describing the breakthrough LT3081 low dropout linear regulator suggests that its constant loop gain improves transient response and absolute output voltage accuracy over other LDO solutions. This statement, although impressive and true, makes an important assumption about engineers’ understanding of loop gain and that there is a clear connection between constant loop gain and the LT3081’s advantages. Unfortunately, loop gain is not as universally recognized as closed and open loop gains.
Without understanding loop gain and its effects on an electronic circuit, the benefits of the LT3081 cannot be truly appreciated. This article is geared towards the power supply engineer, examining the effect of loop gain on gain and phase margin and relating these to a theoretical control system and real analog feedback circuits.
The Basics
The classic analog building block is the op amp, and its behavior can be applied to most feedback control systems. In fact, the performance of many devices can be simplified by modeling them as op amps. We can apply op amp theory to, say, low dropout linear regulators (LDOs) and switching regulators to predict the part’s stability. Figure 1 shows a simplified op amp circuit.

Figure 1. Simplified Op Amp Circuit
The input voltage is applied to an error amplifier that subtracts a fraction (β) of the output voltage from VIN to produce an error signal. Thus the error is
![]()
This error signal is subjected to the open loop gain of the amplifier (A0) to produce the output voltage:
![]()
This is rearranged to find the closed loop gain of the amplifier:
![]()
In most op amp circuits the open loop gain of the amplifier is very high, i.e. much greater than the “1” in the denominator, allowing the closed loop gain approximation:
![]()
Figure 2 shows a traditional op amp circuit, where predictable operation depends on this gain approximation.

Figure 2. Traditional Op Amp Circuit
For any given voltage at the output, if the open loop gain is infinite, the voltage difference between the two input pins (VDIFF) is zero and the op amp regulates to keep both of its input pins at the same voltage. Here, the output is fed back to the input via the resistive divider R1-R2, so the feedback fraction (β) is 0.1 (1k/10k). From the equations above, if the open loop gain is high, the closed loop gain of the circuit approximates to the reciprocal of the feedback fraction so the circuit has a closed loop gain of 10.
This simplified op amp theory is useful in modeling a variety of circuits, holding true for low frequency inputs, but this simple model loses validity at high frequency inputs.
Loop Gain and the Op Amp at AC
The LT1012 op amp features the classic open loop gain vs frequency response shown in Figure 3.

Figure 3. LT1012 Op Amp Open Loop & Closed Loop Gain vs. Frequency
In Figure 3, you can see the open loop gain is large up to 0.3Hz input frequency, thereafter decaying at a rate of 20dB per decade. Although the gain remains very high over a wide range of input frequencies, there comes a point when the open loop gain cannot be considered relatively infinite. That is, when the open loop gain approaches the closed loop gain, the ideal op amp model described above, and the corresponding assumptions we have made about its performance, begins to lose credibility.
Consider the effect of a finite open loop gain on the closed loop gain of the circuit in Figure 2. The feedback fraction (β) is 1/10, so in the ideal op amp model, the closed loop gain is the reciprocal of this, or 10. If our op amp has an open loop gain of 100, the calculated closed loop gain is
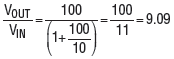
Calculated Closed Loop Gain
The gain is still roughly 10, but with a 9% error.
Now consider using the same amplifier, but with unity gain feedback. The feedback fraction (β) is 1, so ideal op amp closed loop gain should be the reciprocal of this, or 1. If our op amp has an open loop gain of 100, this results in a closed loop gain of

Although the open loop gains of these two circuits are the same, the error in gain is reduced to 1% simply by reducing the closed loop gain.
The equations above show that the error is a function of how large βA0 is in relation to the “1” term in the denominator. Note that open loop gain alone does not always determine the error, but it is the product of the open loop gain (A0) and the feedback fraction (β) that is important. For large βA0, the “1” term loses significance; for βA0 near unity, the “1” becomes significant, increasing the error.
What is βA0
So what is βA0? In Figure 3, the difference between the closed loop curve (approximately 1/β) and the open loop curve (A0), on the log scale is

So the gap between the open loop gain curve and the closed loop gain curve is βA0 (about 105dB at DC). Referring to Figure 1, we can see that A0 • β is the gain going through the amplifier and the feedback loop, so βA0 is our loop gain and is a representation of the excess gain available in the system. Although it is often thought that the open loop gain of an amplifier should be high in order for op amp gain to be accurate, we can see that it is not necessarily the open loop gain, but the loop gain that must be high. In other words, the open loop gain must be high compared to the closed loop gain to get accurate circuit gain.
So what impact does finite open loop gain have on an op amp circuit? Basic op amp theory states that the two input voltages regulate to the same voltage, a suitable assumption at very high open loop gains, but what happens as the open loop gain reduces with increasing signal frequency?
Consider the circuit of Figure 2: as the open loop gain of the amplifier reduces with increasing input frequency, we see an increasing AC voltage between the two input pins equal to the output voltage divided by the open loop gain. This is not the input offset voltage, but a small AC voltage (VDIFF) that is equal to the output voltage divided by the open loop gain of the amplifier. If the open loop gain is one million and we have 1V at the output, then VDIFF is 1µV across the two input pins. As the input frequency goes up and the open loop gain goes down, VDIFF increases. Taken to the extreme, where the open loop gain has decayed to 10, our VDIFF becomes a significant 100mV.
This is where many misunderstand the operation of an op amp at higher AC frequencies, where the two input pins no longer regulate to the same voltage. The voltage between the two input pins consists of the DC input offset voltage (which, for simplicity, we are ignoring here) and VDIFF. VDIFF can usually be ignored, but not at high frequencies.
We know that open loop gain is represented by
![]()
and we know that β is represented by

where V– is the voltage at the inverting input, so loop gain is given by
![]()
Loop gain compares V– (which should be equal to the input signal) to VDIFF.
The Effects of Phase Shift
There is also a phase shift associated with VDIFF. The open loop gain curve of Figure 3 is identical to the response of a low pass filter. There is a break frequency at 0.3Hz after which the gain rolls off at 20dB per decade and another at 1MHz, after which the gain rolls off at 40db per decade. Figure 4 shows a low pass filter with the same break frequencies.

Figure 4. Low Pass Filter With Frequency Response That Matches The Open Loop Gain Curve In Figure 2
The transfer function of a single order low pass filter (made up of R1 and C1) is given by
![]()
As a rule of thumb, for a single order low pass filter, at a tenth of the break frequency the phase shift is roughly zero. At each break frequency, the phase shifts by –45° (a phase lag) and at ten times the break frequency, the phase shift is approximately –90°, remaining there beyond. If the second break frequency is at 1MHz, then at 100kHz, the total phase shift of the filter is approximately –90°, at 1MHz the total phase shift is –135° and at 10MHz the total phase shift is approximately –180°.
Since the open loop gain of the amplifier behaves in the same way, although the input and output voltages of Figure 2 are in phase, there is a phase shift between VDIFF and VOUT associated with the phase shift of the open loop gain of the amplifier. Again, because VDIFF is usually small, we can ignore it, but as the input frequency increases, an increasing VDIFF out of phase with the input voltage might lead to stability issues. The open loop gain curve of Figure 3 presents no stability problems, but it is easy to imagine that if the second break frequency were at a much lower frequency than 1MHz, our circuit would now have an increasing VDIFF that has the potential to be 180° out of phase with the input voltage, which would certainly have stability implications.
LTspice is a useful tool to analyze the effects of phase shift at various frequencies. Figure 5a shows the output voltage lagging VDIFF by 90° at 1kHz.

Figure 5a. VOUT Lags VDIFF in Phase by 90° at 1kHz
If the input frequency is increased from 1kHz to 10kHz, VDIFF increases by a factor of 10, but the phase lag remains 90°, indicating that we are nowhere near the second break frequency of the open loop gain. This is shown in Figure 5b. As the input frequency approaches 1MHz, the phase lag starts to increase above 90° and VDIFF increases accordingly.

Figure 5b. VOUT Lags VDIFF in Phase by 90° at 10kHz
So it can be seen that VDIFF might arrive at a value where it is comparable to the input voltage and 180° out of phase with the input voltage—for a circuit to oscillate, the gain around the loop must be unity and the phase shift around the loop must be 180°. If VDIFF is subjected to the open loop gain of the amplifier (A0), then the attenuation of the feedback network, (β), we can see that it is the loop gain (βA0) and its phase that determine the stability of the system.
Considering the circuit in Figure 2, the op amp amplifies the voltage between its inputs (VDIFF) and this is subjected to gain of βA0 creating a voltage at V–. If the loop gain is 1, this implies that the voltage at V– is the same as VDIFF, thus the amplitude of VDIFF has not changed as it has passed through the loop. If it has undergone a phase shift of 180° and VDIFF has not changed in amplitude, the circuit will oscillate. The purists might argue that the phase shift has to be 360° and this extra 180° is provided by the inverting input pin.
On a side note, if the circuit in Figure 2 has a high gain, this means the feedback resistors attenuate the output voltage by a large amount. The majority of the phase shift occurs in the amplifier (since the feedback resistors have no reactive components, hence present no phase shift), so the lower the gain, the more “phase shifted” output voltage appears at the inverting input, increasing the likelihood of instability. This is why some amplifiers have a minimum gain stability. If you reduce the gain below a certain point, more of the phase shifted output voltage appears at the inverting terminal, so the circuit is more prone to oscillation.
It is worth considering the operation of the circuit in Figure 2 for various loop gains and phase shifts.
At low frequencies, when the amplifier has plenty of loop gain, VDIFF is small and has a phase shift of –90° compared to the voltage at the inverting input (V–). In this situation, the voltage at the inverting input swamps VDIFF, so VDIFF can be ignored. However, if the phase shift of VDIFF is –180° with respect to V–, and there is gain in the loop, we can see that any voltage at VDIFF is amplified as it travels around the loop and inverted, then amplified and inverted, so the circuit oscillates. The circuit only needs to have unity loop gain for oscillations to be sustained. How close VDIFF gets to –180° when the circuit has unity loop gain is a measure of the circuit’s phase margin and tells us how close to the point of instability the circuit’s phase is. A circuit with a phase shift of –120° has a phase margin of 60°.
Likewise, if VDIFF has a phase shift of –180° with respect to V–, but experiences attenuation as it passes through the loop, the voltage arriving back at V– is smaller, so any potential oscillations are stopped due to the lack of loop gain. How much attenuation VDIFF experiences as it passes through the loop (when the phase shift is –180°) is a measure of the gain margin of the circuit and tells us how far below unity gain the circuit’s loop gain is when the phase shift is –180°. A circuit with an attenuation in the loop of 10dB when VDIFF is –180° has a gain margin of 10dB.
All of the above can be related back to control theory and the block diagram in Figure 1. We know that the closed loop gain of a feedback system is given by
![]()
where βA0 is the loop gain of the system. If βA0 has a phase shift of –180° and unity gain, the denominator becomes zero at one particular frequency and the circuit oscillates at that frequency. If βA0 is large, but does not have a phase shift of –180°, the denominator is not zero and the circuit does not oscillate—we have adequate phase margin. Likewise, if βA0 is less than unity but has a phase shift of –180°, the circuit does not oscillate—we have adequate gain margin.
So now we can see that we have related open loop gain, closed loop gain, loop gain, gain margin and phase margin as well as explaining this in the control theory domain and the circuit theory domain.
So how does this relate to power supply circuits? Most power supply systems can be modeled as an op amp circuit. Figure 6 shows the LT1086 linear regulator. We can see that the circuit has two feedback resistors and these provide a fraction of the output voltage to the ADJ pin (which is the inverting input of the internal op amp). The non-inverting terminal is tied to the internal reference voltage.

Figure 6. Traditional Linear Regulator (LT1086)
As discussed above, the accuracy of an amplifier’s gain is determined by the loop gain of the amplifier: more loop gain in an amplifier means more gain accuracy.
Increasing the output voltage of the LT1086 is identical to increasing the closed loop gain of an op amp. Figure 7 shows the effect of increasing the closed loop gain from 20dB to 80dB. If the loop gain is represented by the difference between the open loop gain curve and the closed loop gain curve, increasing the output voltage of the LT1086 reduces the loop gain, reducing the absolute accuracy of the output voltage. Another drawback with increasing the output voltage is reducing the frequency response of the circuit (in this case from 100kHz to 100Hz), so load transient response suffers.

Figure 7. Voltage Gain vs Frequency
The LT308x family of linear regulators changes the conventional LDO architecture to that shown in Figure 8.

Figure 8. LT3080 Linear Regulator Uses an Unconventional Architecture to Improve Accuracy & Transient Response
The LT3080 uses an internal current source to develop a voltage across an external resistor, RSET. This voltage is then applied to a unity gain buffer to produce the output voltage. This has a number of implications.
The internal op amp operates in constant unity closed loop gain, with the output voltage set by the RSET resistor value at the “input” of the op amp.
Compare the LT3080 shown in Figure 7 to the traditional op amp circuit shown in Figure 6. The output voltage of the LT1086 in Figure 6 is altered by changing the feedback resistors (and hence the closed loop gain) of the LT1086. Contrast this to the LT3080 operating in constant closed loop gain, where the “input” voltage to the amplifier is changed, set by the voltage across RSET. If the closed loop gain remains unchanged, the loop gain remains unchanged, so the circuit features good absolute accuracy, even at high output voltages. Incidentally, this is why the loop compensation components in a DC/DC converter always have a series capacitance. The output of the error amplifier is a current source and the series capacitance at DC is high impedance, thus producing high loop gain at DC in the compensation loop.
Another consequence of keeping the loop gain unchanged is that the frequency response remains unchanged, and is not sacrificed at high output voltages, so the part is able to respond quickly to load transients.
Another benefit, of particular interest in light of ever decreasing supply voltages, is that the LT308x parts can produce an output voltage down to 0V. Traditional LDOs cannot set their output voltages lower than the internal reference voltage, whereas by shorting out RSET on the LT308x part, the output voltage can be set as low as 0V.
Conclusion
The LT308x family of LDOs, due to their constant high loop gain, feature better high output voltage accuracy and transient response than traditional LDOs. They also can be used in ways that traditional LDOs cannot, such as setting output to 0V, or paralleling them for higher current operation.




















