摘要
The design differences among five constant-current circuits are analyzed. Performance data are discussed, and illustrate the different compromises between precision, dynamic impedance, and compliance range for some of the circuit designs.
A controlled constant-current source or sink is a useful circuit block to use in designing electronic applications such as sensor bias, amplifier bias, and special waveform generation. These types of circuits exhibit high-output dynamic impedance, while delivering relatively large currents within the specified voltage range.
Constant-current circuits are usually implemented with an op amp and a discrete external transistor. Source, sink, and bipolar versions can also be designed with a single op amp and some resistors (Figure 1). The Figure 1 circuits A, B, and C are constant-current sinks offering different compromises among precision, dynamic impedance, and compliance range. Circuit D is a bipolar current source whose feedback connection is simpler than that of the usual Howland current pump (no positive feedback, constant input impedance). Circuit E is a constant-current source. All circuits in Figure 1 exhibit excellent linearity of output current with respect to input voltage.

Figure 1. Constant-current circuits: current sink (A); current sink (B); current sink (C); bipolar current (sink/source) circuit (D); and current source (E).
The output of Circuit A is uncertain because of the op amp's quiescent current, which adds to the calculated output. (The 25µA quiescent current for the op amp shown, however, is negligible in most applications.) Circuit B behaves similarly to Circuit A, but subtracts quiescent current from the ideal output-current value. Circuit C is a sink with no quiescent current error, and Circuit Dsinks or sources current depending on the polarity of the input voltage (i.e., a bipolar output). The performance of Circuit D depends on good resistor matching for the pairs R1-R2 and R3-R4, and good tracking between the +V and -V power supplies. Any difference between the absolute values of positive and negative supply voltage appears as an offset at zero input voltage.
Circuit E is a current source, which requires close matching of the R2-R3 and R4-R5 resistor pairs to ensure insensitivity to changes in the supply voltage. Output currents for the different circuits can be calculated using the following formulas:
Circuit (A) IOUT = -[VIN/RLOAD + (25µA)]
Circuit (B) IOUT = -[VIN/RLOAD - (25µA)]
Circuit (C) IOUT = -(VIN/RLOAD)
Circuit (D) IOUT = -2VIN/RLOAD
Circuit (E) IOUT = VIN/RLOAD
The formula for Circuit D assumes perfect matches: R3 = R4, R1 = R2 and +V = -V. It also assumes that R3 >> R1.
The data in Figure 2 reference the circuits of Figure 1. Figure 2 shows the dynamic impedance and range of useful output voltage (compliance) for a fixed value of output current. The output current for all plots is 5mA. (A high value was chosen to show the higher end of the current amplitude range.) Depending on the application, you may be able to improve the dynamic impedance and range of these circuits with a judicious choice of op amp and resistor values.

Figure 2. Output current vs. output voltage is illustrated for the circuits of Figure 1. Note that for Circuits B and C, the dynamic output impedance closely resembles an ideal current source: ΔVOUT/ΔIOUT = ∞.
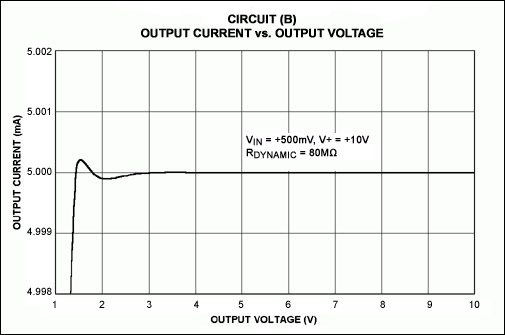
Figure 2. Output current vs. output voltage is illustrated for the circuits of Figure 1. Note that for Circuits B and C, the dynamic output impedance closely resembles an ideal current source: ΔVOUT/ΔIOUT = ∞.

Figure 2. Output current vs. output voltage is illustrated for the circuits of Figure 1. Note that for Circuits B and C, the dynamic output impedance closely resembles an ideal current source: ΔVOUT/ΔIOUT = ∞.
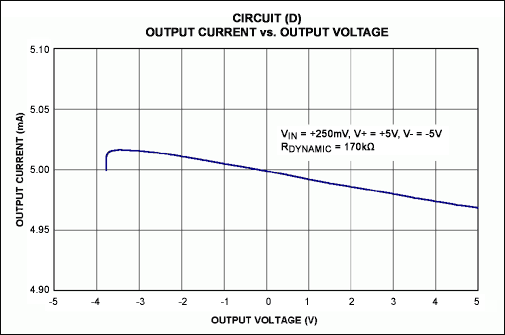
Figure 2. Output current vs. output voltage is illustrated for the circuits of Figure 1. Note that for Circuits B and C, the dynamic output impedance closely resembles an ideal current source: ΔVOUT/ΔIOUT = ∞.

Figure 2. Output current vs. output voltage is illustrated for the circuits of Figure 1. Note that for Circuits B and C, the dynamic output impedance closely resembles an ideal current source: ΔVOUT/ΔIOUT = ∞.
A similar article appeared in the March 2, 2006 edition of EDN.




















