摘要
Electrical engineers designing analog electronics commonly have to drive a capacitive load with an operational amplifier that cannot quite handle the required capacitance. Common approaches to handling this situation have limitations that are not always understood. Using simulation, we show these limitations and how to overcome them.
Associated simulation files are available for download (requires either a purchased or demo version of TINA®, a commercial Spice-based simulator, which can be obtained at www.tina.com).
A similar version of this article appears on EDN, April 28, 2013.
From Ideal to Real: Starting with the Basics
Those of us with experience know that the most common problem with op amps driving capacitive loads is the stability of the loop around the op amp. Figure 1 shows a simple “ideal” op-amp circuit with a gain of -1 driving a 1µF capacitive load.

Figure 1. Basic op amp driving a capacitive load.
Now, if this op amp were ideal, it would have zero output impedance and the load capacitance would have no effect on the stability of the loop around it. As I hope you have figured out, ideal op amps are simply not available in the real world.
Any real op amp has some output impedance. To make things simple for now, we will assume that the output impedance is a resistance. Figure 2 shows this op amp’s output resistance explicitly.

Figure 2. The Figure 1 circuit with op amp output resistance added.
We now have an RC lowpass filter with ROUT and C1. The resulting pole frequency is:
fp = 1/2πRC = 2.122kHz
While an ideal op amp has infinite gain, a real op amp has very high, but finite DC gain. It also has a pole at a fairly low frequency that causes the op amp’s gain to roll off, eventually reaching unity gain at some much higher frequency. This pole is referred to as the dominant pole. There are always more poles, all at frequencies higher than the unity-gain frequency in a well-designed op amp. For most practical purposes, we can perform our analyses by considering only the first of these poles.
Don’t Get “Lost In Spice”
Before we go any further, I want to mention a big caveat about the practical use of Spice models. Throughout this application note we will be using Spice simulations in lieu of actual work in the lab. I do this often because it gives the reader the ability to play with basic circuits and concepts quickly on their computer. It also is a much more efficient means of clearly demonstrating basic concepts and characteristics in a broad scope. Still, the reader must beware, as must anyone who uses simulators, and avoid believing that simulated results are the absolute truth.
Spice only provides results that are, at best, as accurate as the inputs which we provide, such as models for real components, and how we set it up and use it. Spice can and will yield incorrect results if we do not approach it utilizing our practical knowledge and healthy skepticism.
Ultimately, anything that you do in Spice has to be reduced to practice, if you expect it to work properly.
Rest in peace, Bob Pease.
Let’s Get Simulating
Note: You can download the simulation files (ZIP) (requires either a purchased or demo version of TINA®, a commercial Spice-based simulator, which can be obtained at www.tina.com) for all of the following circuits.
We are using a parameterized op amp model that is part of the standard library in TINA, the simulator used for this application note. Figure 3 shows the table of adjustable parameters.

Figure 3. Parameterized op amp model.
This model allows us to change the characteristics of the op amp to suit our needs without spending time searching for a real op amp with the exact specs that we want.
For now, we will use the default parameters. The key ones for us are:
- Open loop gain: 200k (106dB)
- Dominant pole: 5Hz
- Second pole: 10MHz
- Output resistance: 75Ω
Note that the first two items determine the gain-bandwidth product (GBWP) as 1MHz (200k × 5Hz).
Figure 4 shows the open-loop gain and phase of our op amp.
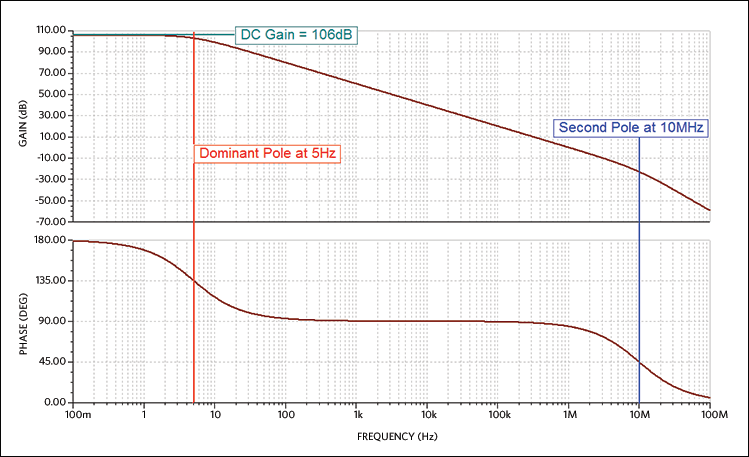
Figure 4. Op amp open-loop gain and phase.
While it is hard to visually resolve on this scale, the gain at low frequency is, indeed, 106dB as promised. We then see a pole, indicated with the red cursor, at 5Hz. Now for a tip: it is easier to identify the precise location of an individual pole by looking at the phase plot for the -45° point rather than the -3dB point of the gain plot. In this case we start with 180° phase (using the op-amp inverting input for consistency with what follows), so the -45° point is 135°.
We also see a second pole at 10MHz, indicated with the blue cursor.
How Does It Work with that Capacitive Load?
Now that we know the salient characteristics of our op amp, we return to our circuit (Figure 1) with a capacitive load. We already know that our op amp has a pole at 5Hz, so that by about 50Hz we only have 90° of margin to work with. Recall that the capacitive load of 1µF combined with our 75Ω output resistance gives us another pole at 2.122kHz. This means that by around 22kHz we should be running out of phase margin. If we have any loop gain remaining here, we will have a very unstable circuit. Let’s take a look.
Figure 5 shows our parameterized op amp in the same circuit as Figure 1 but with some new components added, specifically Vt, Ct, and Lt.
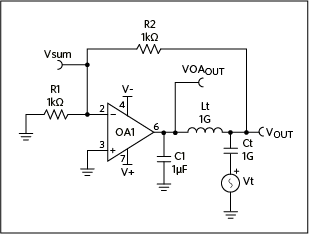
Figure 5. Capacitive load circuit with components to measure the loop.
These additional components are needed to measure the loop without breaking the DC path of the loop. In theory, with perfect op amps, we could disconnect the feedback resistor from the output of the op amp, inject a signal into this disconnected end of the resistor, and measure the output of the op amp in order to see what the loop gain is. However, if the loop is not closed, at least for DC, then small offsets will cause the output to saturate. Remember: the DC gain of our op amp is 200k, so just a 1mV offset results in a 200V output.
We place an inductor with an enormous value, Lt, between the op amp output and the feedback resistor, making sure to keep the load capacitance with the op amp so it will react with the output resistance of the op amp. We then inject a signal into the output end of the feedback resistor using a large-value capacitor, Ct, in series with the signal source. These large component values ensure that the loop is still closed for DC but that these added components will not affect measurements at the frequencies of interest. This approach really only works in “Spice-land,” because we can have components with these large values.
Since we are driving the output of this circuit, the normal input at R1 is grounded. It is time for a quick simulation (Figure 6).

Figure 6. Bode plot of the loop gain for the circuit in Figure 5.
The red cursor in Figure 6 indicates the location of the pole caused by the capacitive load. The blue cursors are at unity gain crossover and indicate a 3° phase margin. Of course, this is terrible for stability.
Making It Stable
In some cases, the solution is simple: put a small-valued resistor between the output of the amplifier circuit and the capacitive load. This added resistor isolates the op amp from the capacitance enough to avoid instability, as shown in Figure 7.

Figure 7. Adding a small isolation resistor isolates the op amp from the capacitance and increases stability.
Keep in mind that R3 is outside of the op amp loop. This means that the op amp’s feedback can do nothing to decrease the resultant output impedance. We can calculate and simulate (measure) this output impedance.
Since we are assuming an ideal op amp here, the output impedance is just the parallel combination of R3 and C2. Even with most real op-amp circuits, until we reach frequencies where the op amp circuit runs out of loop gain, the output impedance will be dominated by these components. In this circuit the relatively large capacitance of C2 means that its impedance will be so low at those higher frequencies that it alone will dominate. Therefore, the output impedance is given by Equation 2:
ZOUT(s) = R3/(1 + C2R3s)
We can use a special meter in TINA, the Z-Meter, to measure (actually simulate) the output impedance of our circuit. The Z-Meter actually includes a source and measuring element, so we have to eliminate our input signal and ground the input. Figure 8 shows the modified schematic.

Figure 8. Adding the Z-Meter to measure the output impedance.
Now, we can just run an AC analysis and see what the Z-Meter reports. By default, the magnitude of the impedance will plot with a linear y-axis. It is more instructive to change that to a logarithmic scale to make it clear that we are dealing with a simple pole. Figure 9 shows this impedance plotted like a voltage transfer function, displaying a single-pole response with a pole frequency of 3.18kHz.

Figure 9. The output impedance of the Figure 8 circuit.
Now, for some circuits, this may be a fine result. However, if there is a resistive part of the load as well as the capacitance, then we just added a new error term in the form of a voltage-divider at all frequencies, including DC.
If we cannot have this 50Ω output impedance at DC and low frequencies, then we might want to lower the output impedance with feedback. Our first instinct may be to connect the output side of the feedback resistor, R2, to the circuit output, not the op amp output, thereby enclosing R3. But that just puts us back in the same situation where we started.
Adding a Second Feedback Loop
If we add another capacitor to the mix to close a second feedback loop around the op amp, we can have the feedback resistor connected to the circuit output and still have a stable circuit. Figure 10 shows this configuration.

Figure 10. A dual feedback path is created by adding another capacitor, C1.
There is a simple way to explain how this circuit works. The feedback capacitor, C1, is used to close the loop for the higher frequencies while the feedback resistor, R2, is used to close the loop for DC and lower frequencies. There exists, of course, a crossover frequency region in between. To start, the value of C1 is chosen such that R3C2 = C1R2. Why? Well, frankly, this is experience-based intuition.
We first look at the forward transfer function from VIN to VOUT. The transfer function in the Laplace domain is fairly easy to determine, but there is an interesting feature of TINA: symbolic analysis. As long as we use an ideal op amp, TINA can provide the transfer function equation.
Figure 11 shows what the AC transfer symbolic analysis function returns:

Figure 11. Symbolic analysis results.
This equation is correct. However, it is not in a form that best displays the salient feature, i.e., a “low entropy” form of the equation. Some simple algebraic manipulation results in Equation 3:

Here we see that the DC and low-frequency gain is –R2/R1 and that there is a complex-pair pole to roll off the higher frequencies. The Bode plot of this transfer function is shown in Figure 12.

Figure 12. The Bode plot of the transfer function.
Figure 12 indicates that the transfer function is a rather well-behaved second-order lowpass response with just slight peaking.
We seem to have completely resolved the issue of our op amp driving the capacitive load. We have a well-behaved circuit in a configuration with two feedback paths, one that keeps DC and low frequencies within a closed loop and another that does the same for the higher frequencies. I guess that means, “It’s beer time.”
Not So Fast, Buddy—Put that Beer Down!
Are we being overconfident? Too hasty? Let’s make sure that everything is as good as we believe. First we need to check out the loop to verify that it is stable. Figure 13 includes the same additional components used in Figure 5 that are needed to measure the closed loop.

Figure 13. Modified circuit for loop measurement.
The AC results for this circuit are shown in Figure 14 and indicate that we have more than 50° phase margin.

Figure 14. Loop gain plot shows over 50° phase margin.
No, it is still not beer time. We assumed that the two loops handled the output impedance across all frequencies, but perhaps there will be some peaking of that impedance near the crossover of the two loops?
We use our handy Z-Meter again and take a look. As before, we short out the input and connect the Z-Meter to the output of our circuit, as shown in Figure 15.

Figure 15. Measuring the output impedance of the dual-loop design.
The result is a second-order bandpass function with a peak of 50Ω shown in Figure 16.

Figure 16. Output impedance for the dual-loop circuit.
To gain better insight into the output impedance, we examine its equation. In looking at Figure 15, it is clear that the output impedance is going to be C2 in parallel with the output impedance of the circuit without C2. So we start by calculating that latter part.
Note that the op amp, R2, and C1 constitute an integrator with VOUT as the input. The output of the op amp is thus:

The voltage across R3 is VOUT - VOPAMP_OUTPUT, which means that the current through R3 is:

From this result, we can determine that the effective impedance of R3 from the output point of view (keeping in mind that it is driven by the integrator on its other end) is:

Of course, R2 connects between the output and a virtual ground, so it is in parallel with this impedance. Combining it with the result of Equation 6, we get:

Now we can factor back in the load capacitance, C2, in parallel with this result to get the output impedance of the entire circuit:

What does this equation tell us? No matter what we do, there will be a frequency at which the output impedance will equal R3. That frequency will be at the peak of a second-order bandpass type function.
Examining This Effect over a Wider Range of Conditions
For kicks…I mean for educational purposes…let’s vary C1. This will move the peak frequency around and vary the Q of the circuit. Figure 17 plots the output impedance for 20 different logarithmically spaced values for C1 from 500pF to 5µF.

Figure 17. Output impedance by varying C1.
With the larger capacitance, we have a very heavily damped response with a broad peak. As we lower the capacitance, we get to a very high-Q peaked response. The interesting behavior, of course, is that the peaks are all right at ZOUT = 50Ω. Keep in mind, however, that this is the ideal case with a perfect op amp that has infinite gain at all frequencies. It is instructive to examine such an ideal case to isolate this behavior from other effects. Shortly, we will look at more realistic cases.
Before we do that, we should consider the transfer function of this circuit. Since the impedance is peaking sharply with low values of C1, we would expect to see similar peaking in the frequency response of the circuit. Figure 18 shows both amplitude and phase of the frequency response of our circuit with C1 varying.
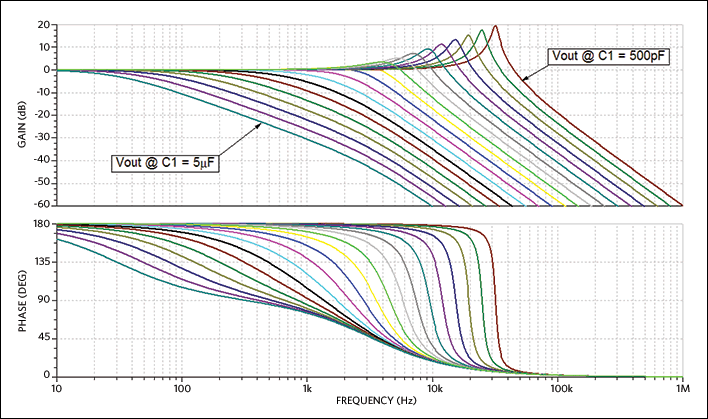
Figure 18. Frequency response of the Figure 15 circuit as C1 varies from 100pF to 1µF.
The output impedance showed us a family of second-order bandpass curves from low to high Q. Now the frequency response is, as expected, a second-order lowpass and the Q varies just as widely as it did for the output impedance.
Even though we verified that we will have peak output impedance equal to the output resistor, we do have some design freedom to move it in frequency and affect the shape, the Q, of the peak by varying component values. Of course, the frequency response will change accordingly as well.
Getting a Bit More Real
Before we forget, we can use our more realistic, parameterized op amp model and run similar simulations for the output impedance with C1 varying. Figure 19 is the equivalent of Figure 17 using the parameterized op amp with a GBWP of 1MHz.

Figure 19. ZOUT with a 1MHz GBWP op amp.
Notice how as the peak moves to the right it raises above 50Ω. Also note that the horizontal spacing between traces is compressed as we move to the right. Both of these effects are due to the op amp running out of gain as frequency increases. We see something very similar in the frequency response shown in Figure 20.

Figure 20. Frequency response with 1MHz GBWP op amp.
Now let’s increase the bandwidth of the op amp by a factor of 10. For this parameterized model, we just increase the values of the dominant and second pole by factors of 10. We will just look at the output impedance since we know that the frequency response will behave similarly. Figure 21 shows the output impedance using an op amp with a GBWP of 10MHz.

Figure 21. Increasing GBWP to 10MHz.
With the GBWP increased to 10MHz, we can only detect very slight increases in the peak for the lowest few values of C1. This would appear to be an adequate GBWP for our purposes.
So it looks like we have a firm understanding of this situation. We know that, while we can get very low output impedance across a very broad range of frequencies, there will always be a peak of at least the output resistance of the circuit with the outer loop open. We make every effort to get that resistance set as low as possible, but we are stuck. If we set it too low, as we saw earlier in this application note, the op amp becomes unstable. If we need lower output impedance than this, we need another tactic.
There Is a Real Application for All This
This is a real situation that I faced 25 years ago trying to interface a reference to a pin on an IC that required a minimum capacitance (the 1µF load cap) and a low impedance (less than 5Ω) from DC to 100MHz or so. The high-frequency range is no problem, as the output impedance plots show. Of course, any 1µF capacitor is likely to self-resonate at a few to a couple 10s of MHz. But we can handle this by paralleling it with smaller value caps that have higher resonant frequencies, a common practice.
But, how do we decrease that peak in the output impedance of our circuit which is now 50Ω? A simple solution is to use an emitter-follower circuit to drop the output impedance of the op amp with the added resistor. Figure 22 shows the addition of such a circuit. Note that we need not worry about the voltage drop across the base-emitter PN junction, as our DC feedback loop corrects for it.

Figure 22. Adding a follower.
Here are a couple quick observations about this circuit. We picked a low-cost transistor with a relatively low emitter resistance spec. However, we have to recognize that the emitter resistance increases with lower current. This is why we need the 1k resistor to V-, i.e., to set the emitter current high enough for our needs. Since the added transistor does, in fact, buffer the output, we can decrease R3 as well. C3 is added just for good practice to filter out noise ahead of the buffer.
Figure 23 shows the simulated output impedance using our Z-Meter.

Figure 23. Output impedance with the added follower.
There is a price, a trade-off for lowering the peak impedance: the power dissipated while supplying the current for the follower is about 50mW. To demonstrate the importance of this current for lowering the output impedance, we double the current and, thus, the power dissipation by decreasing R4 by half to 500Ω. Figure 24 is the output impedance plot with this change to R4. Notice that the peak impedance has been cut nearly in half.

Figure 24. Output impedance with twice the emitter current.
Of course, good engineering practices require us to check the frequency response and loop gain of this circuit, as we have done before. Figure 25 demonstrates a well-behaved frequency response.

Figure 25. Transfer function frequency response of final circuit.
The loop gain of the entire circuit was simulated as for earlier versions of the circuit. The results are shown in Figure 26. We can see that there is nearly 90° of phase margin and the curves are well behaved, so this would appear to be a very stable design.

Figure 26. The loop gain of the final circuit indicates a stable design.
Some Final Observations
Now, of course, the next step would be to verify all of this in the lab with real circuitry to ensure that we get the expected performance. The author built this circuit many years ago and verified proper operation.
In these days of high integration with millions of transistors on a chip, sometimes we still need to use a single discrete transistor to get the job done. To make a circuit work properly, though, we have to rely on our fundamental knowledge of basic electronics. These basics, an inquisitive mind, and a healthy dose of skepticism have always been needed, but are even more critical today with our sophisticated products and tools.




















