AN-1386:ADC中采样时钟频谱对实测信号频谱的影响简单数学描述
简介
现代高速模数转换器(ADC)的性能直接取决于其时钟。然而,信号发生器中用来产生这些时钟的振荡器并非理想器件,时钟幅度和相位均有可能偏离理想值。ADC采样电路对较小的时钟幅度变化往往有很好的抵抗力,但即使很小的相位偏移也可能对ADC输出带来严重影响。因此,使用高速ADC时,若要获得准确的读数,必须认真研究时钟振荡器的相位噪声。
本应用笔记提供一个已经完全确立但在实践中很少使用的数学背景说明,这是了解时钟和模拟输入相位噪声的影响所必需的。本文讨论幅度噪声和相位噪声的异同,通过简单的公式来估计边带功率,并澄清将时钟和模拟输入噪声耦合到实测ADC信号的机制。
最后,本文以AD9684为例,说明如何应用这些方法来评估现代高速ADC及其性能。
幅度噪声与相位噪声
正弦波是高速ADC的主要时钟波形,因为与方波等其他波形相比,它更易于产生、传输以及匹配RF频率。在数学上,正弦波可以描述如下

其中:
c(t)为载波(时钟)。
Ac为载波幅度。
ωc为角频率。
t为时间。
通常,时钟信号是高功率(>13 dBm)信号,有助于减轻电缆、连接器和走线上的损耗。可以放心地假设:时钟功率高于噪声功率。
三角函数近似计算
当x < < 1时,本应用笔记中大量使用如下近似公式。因此,必须知道这些方法何时不再可行,以及之后会发生什么。x值越大,这些简单的线性近似产生的误差也越大,如图1所示。

确定性方法
第一个话题是时钟噪声,在下面的证明中,假设它是正弦曲线。通过这种简化,我们可以研究载波与噪声之间的相位。幅度噪声以幅度调制(AM)的形式来讨论。

其中:
cAM(t)为带AM噪声的载波(时钟)。
Ac为载波幅度。
An为噪声幅度。
ωn为噪声角频率。
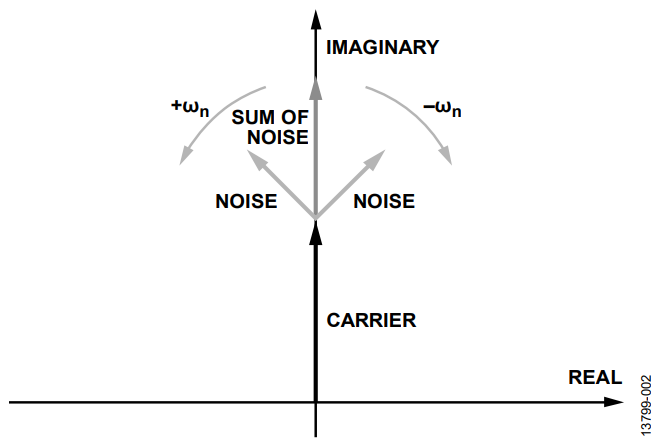
注意,AM产生两个分量:一个低于载波频率,一个高于载波频率。因此,通常将这种调制称为双边带(DSB)。这两个分量的相位也与载波相位对齐,它们全都是正弦曲线。
图2中的信号相量图以更直观的方式揭示了相位关系。 sinωct 载波处在90°相位,方向为垂直向上。相比于作为参考的载波,两个噪声分量以ωn的角速度沿相反方向旋转。因此,其和始终是一个与载波共线的矢量。换言之,幅度噪声总是与载波同相。图3所示为这种AM调制信号的频谱

下一个话题是相位调制(PM)形式的相位噪声。
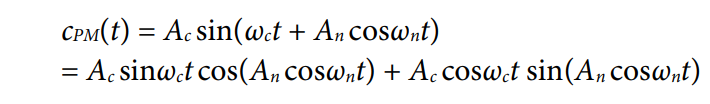
在此情况下, An可被称为相位调制指数。如果 An << 1,则

这样就可以简化PM等式:

两个噪声分量的频率与AM-DSB情况相同。唯一不同的是相位,其与AM-DSB信号相差90°。因此,其和始终与载波正交。相量图和信号频谱有助于我们形象地了解信号(参见图4和图5)。
该图还显示了频谱分析的一个固有问题:AM-DSB信号和低调制指数PM信号的频谱不可区分。AM和PM噪声常常同时存在,实测频谱是其各自频谱的结合。
随机性方法
噪声不是确定性的,多数情况下也不是正弦曲线。因此,分析的下一个话题是随机噪声的功率频谱密度(PSD)。该频谱包括负频率,这与电信领域分析信号的惯例是一致的。
假设噪声函数n(t)的期望值为0,即E[n(t)] = 0,并且其DSB PSD为ν(ω),即ν(ω) = ν(−ω)。
从AM噪声信号开始,
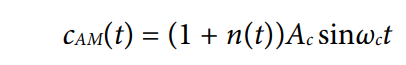
如果将其傅里叶变换定义为

其中,T为周期时间。
那么,其PSD等式可以表示为:
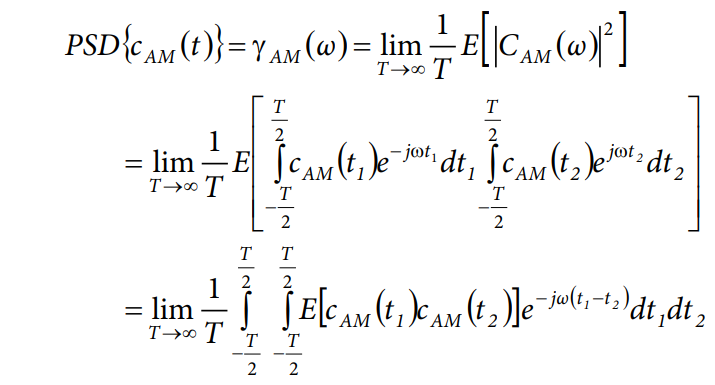
关健部分是积分中的期望值表达式,对其单独处理。
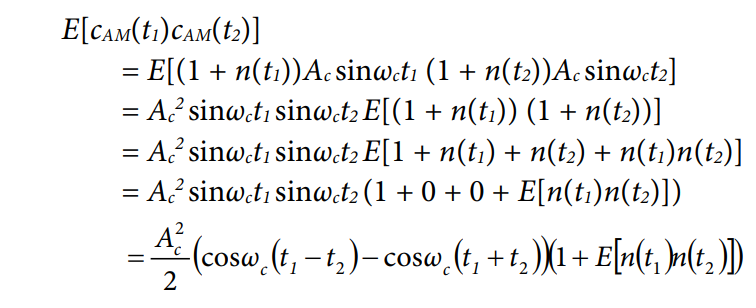
t1和 t2变量用τ = t1 − t2和υ = t1+ t2替换。假设E[n( t1)n( t2)]仅取决于时间差;因此,它可以用自相关R(τ)来代替。
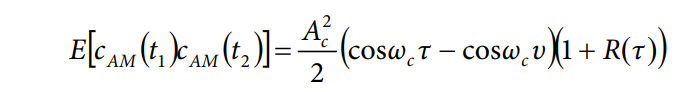
可将此结果代入PSD计算中。多重积分中改变变量的规则要求表达式乘以雅可比矩阵的行列式值,本例中为1/2。请注意,变量改变也会影响积分限。
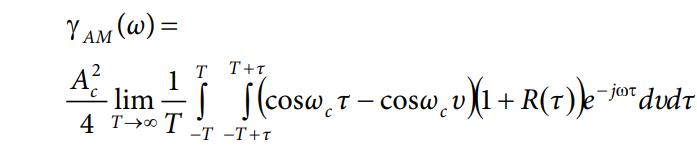
仅(cosωcτ − cosωcυ)取决于变量υ;因此,可以对其单独积分。

这样就可以进一步简化PSD表达式。

该结果与前述结论一致。信号频谱主要包括两个部分:第一部分是角频率为 ωc的纯载波,用两个狄拉克δ函数来表示——针对正频率的δ(ω − ωc)和针对负频率的δ(ω + ωc);
第二部分是噪声信号本身的DSB PSD,也混频到ωc(参见ν(ω − ωc)和ν(ω + ωc))。其缩放比例为Ac2/4,对频谱的任何绝对测量都包括该因子。但在实践中,实测噪声在功率上会还原,并且基于实测载波移回到DC,从而避免这种相关性。结果便是原始噪声PSD ν(ω),现在称为相对于载波的噪声PSD。
接下来研究相位调制。

如果n(t) << 1,

这样就可以将表达式简化为:

其PSD等式可以表示为:
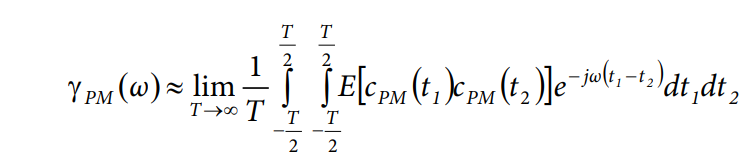
关健部分是期望值,对其单独加以研究。

第一部分是纯载波,与前述证明相同;因此,只需关注第二部分。t1和t2变量用τ = t1 − t2和υ = t1 + t2来代替,E[n(t1)n(t2)] = R(τ)。第二部分为
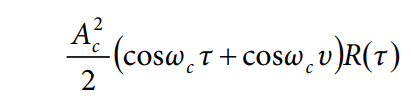
对υ变量单独积分,

将此等式代入PSD计算中,

最后,把所有部分放在一起,

我们再次看到,信号频谱由角频率为 ωc的纯载波和混频到 ωc的噪声信号本身的DSB PSD组成。但在这种情况下,混频是由余弦函数加上90°相移来实现。
后果
确定性相量和随机方法均揭示了相同的影响深远的后果。首先,对于低调制指数PM信号,边带与调制指数直接相关。考察边带功率就会揭示相位噪声功率。
其次,任何加性噪声矢量都可以被解释为AM噪声(与载波同相)和PM噪声(与载波正交)之和。如果关注的是PM噪声,则必须消除AM分量,然后根据边带功率估计相位噪声功率。
第三,该证明仅对调制指数较Low PM Modulation Index Criterio低的情况有效。在其他情况下,边带功率与相位噪声功率没有直接关系,依据此结论进行估算有着内在的缺陷。
低PM调制指数准则
正弦和余弦函数的泰勒级数揭示了调制指数较高时会发生什么。噪声函数进入非线性区,对于简单的确定性正弦噪声,其为如下:

除边带中的附加功率外,等式中的三次幂、五次幂等项会产生谐波,PSD计算变成贝塞尔积分。根据前述证明可以写出从属等式,但很繁琐,等式很长,没什么意义。其结果是,边带功率变得高于PM噪声功率,后者不能用前者来估算。然而,高低调制指数之间并没有清晰的界线,简单近似可行与否要由用户决定。
边带功率
利用频谱分析仪研究非理想时钟,得到的不是单一无限窄的尖峰。相反,它有连续的边带,后者逐渐消失在没有明确界限的噪底中。需要考虑的问题如下:
- 要对多少边带功率进行积分?
- 噪底是否是边带功率的一部分?
第二个问题很容易回答:只需比较有和无输入信号两种情况下的噪底。频谱分析仪的噪声与时钟噪声无关,因而不予考虑。
第一个问题需要进一步讨论。首先需要确定噪声带宽。人们很容易只考虑信号的低频、高功率PSD区间,但最终积分的区间是很宽的,超低功率宽带噪声的贡献可能比低频噪声的贡献还大。
此外,由于宽带部分很可能来源于热噪声,可以想象它是白噪声,因而具有无限能量。幸运的是,在大多数实际电路上,寄生电容和等效电阻的组合形成一个低通滤波器(LPF),它会在同一点引入滚降,从而降低该能量。
为了对此功率进行量化,假设信号PSD σ(f)由多个分段组成,其形式为σ(f) = αfβ或 σdB(f) = 10log10α + β10log10α。(注意这里使用的是常规频率f,而不是角频率ω;后者更适合于讨论正弦波,但测量的通常是前者。)也可以考虑其他形式,但该形式可以方便地使dB与十倍频程的关系曲线成为直线。利用一个分段上的任何两点,便可计算其α和β参数。β表示PSD的陡度;因此,若 β = −2,则陡度为−20 dB/dec。

分段下的功率可利用以下积分计算:

若β ≥ −1,则具有无限带宽(即 f2 = ∞,简单热噪声模型就是这样)的噪声将导致无限功率。然而,若β < −1, f2 + 1 = 0,功率将是有限的,可以计算如下;
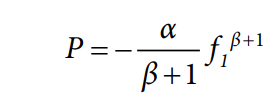
抖动和相位噪声
时钟
首先通过简单混频来研究时钟相位噪声耦合(参见图6)。
这种情况下,与时钟相乘得到理想频率转换,信号频谱移至时钟频率。
非理想时钟会影响输出频谱(参见图7)。时域中的乘法相当于频域中的卷积。这种现象称为倒易混频,在射频(RF)收发器设计中特别重要;一个具有高相位噪声的不适当时钟可能导致混频信号泄漏到相邻射频通道中。
非理想时钟会影响输出频谱(参见图7)。时域中的乘法相当于频域中的卷积。这种现象称为倒易混频,在射频(RF)收发器设计中特别重要;一个具有高相位噪声的不适当时钟可能导致混频信号泄漏到相邻射频通道中。
然而,对于ADC采样时钟,理想和非理想乘法模型均无法准确描述时钟噪声耦合机制及相关抖动。最简单的采样模型假设,时钟的每个上升沿产生一个理想采样脉冲(参见图8,注意时钟的时域和频域表示以及采样脉冲串均有显示)。此脉冲串在时域中与输入信号相乘,得到采样输出。
注意:输入信号与时钟不是直接相乘,因此,其频谱之间不存在直接卷积。与信号频谱卷积的是采样脉冲串的频谱。脉冲串的频谱在频域中也是脉冲串,由此产生广为人知的如香农-奈奎斯特采样原理所述的周期输出频谱。该理论证明:若采样频率足够高,采样输出信号就能精确表示连续输入信号。
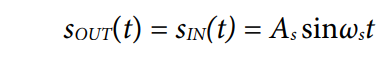
其中:
sOUT(t)为输出信号。
sIN(t)为输入信号。
As为信号幅度。
ωs为信号角频率。
确切地说,这一论断仅在采样时间点成立;因此,这里必须使用lTc,而不是t,二者分别代表离散时间和连续时间。然而,为了简洁起见,大多数情况下是使用t。
利用该模型,抖动便是时钟相位噪声的一个自然产物。
相位噪声会在时间上移动采样脉冲,使其偏离理想位置(参见图9)。相对于理想时钟的这种偏差称为时间间隔误差(TIE) tj(t),它是一个很好的数学模型,但难以测量。通常测量的是连续脉冲之间的时间,以获得周期或周期间抖动,然后通过周期抖动计算TIE。注意:抖动从根本上讲是一个离散时间概念,仅在采样时刻有意义。
TIE与相位噪声之间的关系很简单。时钟周期Tc对应于一郑权,角度为2π。
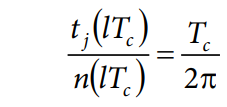
修改的采样脉冲串的频谱难以用分析方式表示,因而输出频谱也无法表示。可以讨论的是抖动引起的瞬时加性误差,假设输入信号为正弦波(参见图10)。

注意,使用的是t而不是 lTc,这仅仅是为了简洁起见。
假设 ωstj(t) < < 1,这样便可使用之前讨论的近似。

注意 ωstj(t)可以简化。

因此,可以获得以下的简单关系:
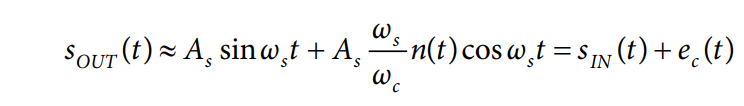
其中,ec(t) 为时钟抖动引起的加性误差。
此结果有着深远的后果。考虑到近似,DSB时钟相位噪声 n(t)直接映射在输入信号周围。时钟信号的频谱被直接复 制到输入信号上,与倒易混频的情况非常相似。但是,耦 合机制不同,功率也不同,原因是As(ωs/ωc)为常量。
利用该结果还可以进行比较。若满足以下条件,则两种采样解决方案就抖动噪声功率而言是等效的:

反之,若利用一个具有与频率无关的固定相位噪声特性的假想信号发生器来产生时钟,则以较高的频率运行它时(即以较高的速率采样),抖动噪声功率会降低。
模拟输入
到目前为止,本应用笔记忽略了输入信号本身也需要产生以及该过程也是非理想的这一事实,因此,导出的结果不完全准确。然而,现在已经有了描述这种系统的工具。第一步是承认输入信号也有相位噪声m(t)。输入和时钟相位噪声是独立的。

m(t + tj(t))部分可利用几条假设来予以简化。信号相位噪声 的形状可能是频域中的一个尖峰,这相当于一个非常宽的 自相关函数。换言之,在任意给定时间,信号相位噪声与 之前和之后的值非常相似。此外,tj(t) << 1,因此可以假 定m(t + tj(t)) ≈ m(t)。

Asωs⁄ωcn(t)m(t)sinωst 部分可能是可以忽略的。

其中,es(t) 是信号相位噪声引起的加性误差。
同样,结果是一个异常简单的关系。要考虑信号相位噪声,只需加上它即可。
最后考察此信号的PSD。不同部分是无关的,因而功率可以相加。
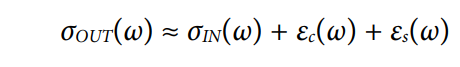
其中:
σOUT(ω)为输出信号的PSD。
σIN(ω)为输入信号的PSD。
εc(ω)为时钟抖动引起的加性误差的PSD。
εs(ω)为信号相位噪声引起的加性误差的PSD。
若展开,则PSD表示如下:

相对于满量程的结果
以上说明在数学上是正确的,但用在实际情况中会有些麻烦,因为绝对信号功率PIN = As2/2可能是不知道的。信号发生器可以设置为熟知的值,但不一定知道ADC输入端的实际信号水平是多少。在信号实际到达ADC输入端之前,损耗、衰减、反射和其他因素都可能影响信号。因此,不是使用绝对功率数值(mW),而是使用相对值。输入信号功率表示为其与输入端满量程(FS)正弦波信号功率的比值。
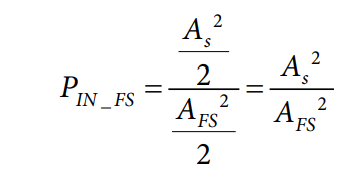
这样,PSD变为

前面提到,信号发生器DSB相位噪声PSD,即ν(ω)和μ(ω)不是用绝对数值来衡量,而是用相对于载波的值来衡量:时钟的标称时钟信号功率和模拟输入的标称模拟输入信号功率。
最后,将正负分量相加,便可将结果整合为只有正频率。

示例
抖动有确定性和随机性两个子类。本应用笔记中的证明尽可能不设限制,使得导出的结果具有普遍适用性,可用来预测各种情况下的信号频谱。
交错式ADC时钟偏斜抖动—应用理论解释复杂ADC的行为
例如,对于时间交错转换器,多个相同ADC处理样本的速率要快于单个转换器的工作采样速率。结果,虽然阵列中的各ADC是以较低速率采样,但总的净采样速率会更高。因此,假如四个100 MSPS ADC交错运行,原则上可以实现400 MSPS ADC。
但是,这取决于各ADC是否有精密而准确的时序。实际应用中可能出现不同ADC的时钟之间有偏移的情况。一般将这种偏移称为时钟偏斜,可以将其解读为确定性抖动或TIE;它不断重复,产生独特的tj(t)函数。利用前面说明的理论,可以解释和预测其频谱。相位噪声直接映射到输出信号上,表示为 As(ωs/ωc)。因此,研究输出频谱便足以判定交错ADC的时序是否有偏移。
SMA100A信号发生器和AD9684 ADC—应用理论预测频谱
下面的例子采用Rohde & Schwarz SMA100A信号发生器(9 kHz至3 GHz)作为高速ADCAD9684的输入时钟。模拟输入由相同类型的信号发生器提供。500 MHz时测得的相位噪声如图11所示。
借助其他输入参数(125 MHz输入频率、−2.0 dBFS输入功率水平、14位分辨率、80 fs孔径抖动、1.9 LSB rms输入白噪声、FFT大小为131072),可以估计输出频谱(参见图12)。
此设置的实际测量数据如图13所示。对于本例,数学预测(显示为细的灰线)同实际测量结果符合得很好。要知道,AD9684 ADC采用多级流水线架构,具有复杂的模拟和数字信号处理功能,但其行为却可以利用图9所示的简单模型和“相对于满量程的结果”部分给出的最终方程进行预测。