Σ-Δ ADC のトポロジーに関わる基本原理: パート 1
Read other articles in this series.
シグマ・デルタ(Σ-Δ)ADC は、今日の信号アクイジションおよび処理システムの設計者が使用するツール・キットの中核となる要素です。本稿の目的は、Σ-Δ ADC トポロジーの基本原理に関する基礎知識を提供することにあります。ADC サブシステムの設計に関係するノイズ、帯域幅、セトリング時間、その他あらゆる重要パラメータ間のトレードオフの例について解説し、高精度データ・アクイジション回路の設計者向けにその背景を解説していきます。
一般的に ADC は、Σ-Δ 変調器とデジタル信号処理ブロック(通常はデジタル・フィルタ)の 2 つのブロックで構成されます。Σ-Δ ADC のブロック図と重要な概念を図 1 に示します。
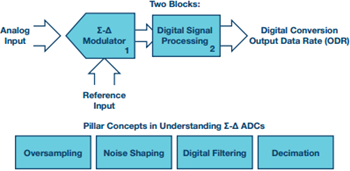
図 1. Σ-Δ ADC の中心概念
Σ-Δ 変調器はオーバーサンプリングを用いるアーキテクチャなので、まずはサンプリング理論と、ナイキストおよびオーバーサンプリングによる ADC 動作のシナリオから考えていきます。
ADC のナイキスト動作を、オーバーサンプリングする場合および最終的に Σ-Δ 変調を行う(オーバーサンプリングも行う)場合と比較したものを、図 2 に示します。

図 2. ナイキスト動作の比較
図 2a は、純粋にナイキスト動作を行う ADC の量子化ノイズを表しています。この場合、量子化ノイズは ADC の LSB サイズによって決まります。FS は ADC のサンプリング・レートであり、FS/2 がナイキスト周波数です。図 2b も同じコンバータを示していますが、こちらはオーバーサンプリングを行っているので、より高いサンプリング・レートが使われています。サンプリング・レートが K 倍になっているので、量子化ノイズの帯域幅は K × FS/2 まで広がります。ローパス・デジタル・フィルタ(通常はデシメーションを伴う)は、青で示した領域より外の量子化ノイズを除去します。

図 2a. ナイキスト・シナリオ。FS でサンプリング、ナイキスト帯域幅は FS/2。
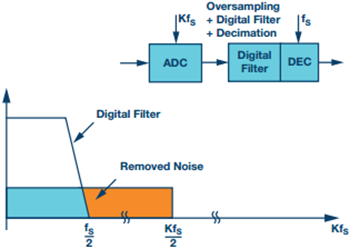
図 2b. オーバーサンプリング・シナリオ。サンプリング周波数は K × FS。
Σ-Δ 変調器は、図 2c に示すようにノイズ・シェーピング機能も備えています。A/D 変換の量子化ノイズはこの変調方式によってシェーピングされ、低帯域幅からより高い周波数にシフトして(一般的な例)、ローパス・デジタル・フィルタによって変換結果のノイズが除去できるようになります。Σ-Δ ADC は、熱ノイズによって決定されるノイズ・フロアで設計することが可能で、量子化ノイズには制限されません。

図 2c. Σ-Δ ADC シナリオ。オーバーサンプリングとノイズ・シェーピングを実行、サンプリング周波数は FMOD = K × FODR。
サンプリング、変調、フィルタ
Σ-Δ ADC には、内部または外部のサンプリング・クロックが使われます。多くの場合、ADC のマスター・クロック(MCLK)は変調器に使用する前に分周されます。ADC のデータシートを参照するときは、この点に留意したうえで変調器の周波数を理解する必要があります。サンプリング周波数 FMOD は、変調器に渡されるサンプリング周波数の値に設定されます。変調器はデジタル・フィルタへの入力データをこのレートで出力し、デジタル・フィルタ(通常は何らかのデシメーションを行うローパス・フィルタ)は出力データ・レート(ODR)でデータを提供します。この流れを図 3 に示します。

図 3. Σ-Δ ADC の処理フロー: サンプリングした変調器出力をデジタル・フィルタを通じて出力。
1 次 Σ-Δ 変調器の詳細
Σ-Δ 変調器は負帰還システムで、クローズドループ・アンプに類似しています。ループには、低分解能の ADC と DAC、およびループ・フィルタが含まれています。出力と帰還の量子化は粗く、多くの場合はハイまたはローの 1 ビットのみが出力されます。基本構造は ADC 用のアナログ・システムとして実装され、ここでは量子化器がサンプリングを行うブロックです。ループの安定化のための条件が存在する場合、その出力は入力を大まかに表すものになります。デジタル・フィルタはこの大まかな出力を取り込んで、アナログ入力を正確なデジタル表現に再構成します。
サイン波入力に対する 1 の出現頻度を示す出力を図 4 に示します。変調器出力のローレベルからハイレベルへの変化率は、入力の変化率に依存します。サイン波のフルスケール出力時は、変調器出力のスイッチング・レートが減少して出力 +1 の状態が支配的になります。同様にサイン波が負のフルスケールのときは +1 と –1 の間の遷移が減って –1 出力が支配的になります。サイン波入力の変化率が最大のときは、+1 と –1 の間の切替え頻度が最も高くなります。出力の変化率は入力の変化率に従います。アナログ入力を記述するのは Σ-Δ 変調器出力の遷移率です。

図 4. Σ-Δ のサイン波入力に対する 1 の出現頻度。Mod 1 Σ-Δ ループの線形モデル (a)
システムは、この 1 ビット変調器(Mod 1)を記述するための線形モデルを使用して、負帰還を行う制御システムとして表されます。量子化ノイズは量子化器の入力と出力の差です。ローパス・フィルタは入力デルタ・ノードの後に置かれます。図 5b では、N の項で量子化ノイズが記述されています。

図 5. Mod 1 Σ-Δ ループの線形モデル (b) と式、フィルタ、信号、およびノイズ伝達関数プロット。
H(f) はループ・フィルタの関数であり、ノイズと信号両方の伝達関数を決定します。H(f) は一種のローパス・フィルタ関数で、低周波数(対象となる帯域内)では非常にゲインが大きく、高周波数では信号を減衰させます。ループ・フィルタは、単純な積分器として、あるいは複数の積分器を直列に接続した形で実装することができます。実際には帰還経路に DAC を配置してデジタル出力信号を取得し、それをアナログ入力のデルタ・ノードへ帰還させます。
図 5 に示す式を解くと、信号とノイズの伝達関数が得られます。信号伝達関数は、対象となる帯域幅内でゲイン 1 のローパス・フィルタとして動作します。ノイズの伝達関数はハイパス・フィルタ関数で、ノイズ・シェーピングを行います。DC 付近の低周波数では量子化ノイズが大幅に抑制され、対象となる帯域幅をはずれた高周波数では量子化ノイズ信号が増加します。1 次変調器(Mod 1)では、およそ 20 dB/decade でノイズが増加します。
システムの分解能を上げるための一般的な方法は、2 個のループ・フィルタを直列に接続してループ・フィルタの次数を上げることです。これによりループ・フィルタ全体としての H(f) はロールオフが大きくなり、ノイズの伝達関数は変化率が 40 dB/decadeの Mod 2 スタイルとなります。量子化ノイズはより効果的にシェーピングされ、周波数ノイズが大幅に減少します。Mod 1 および Mod 2 の Σ-Δ ADC の比較を図 6 に示します。Σ-Δ 変調器のバリエーションとスタイルは多岐にわたります。高次シングル・ビット・ループの安定性に関する問題を回避するために使われるアーキテクチャは、マルチステージ・ノイズシェーピング変調器(MASH)アーキテクチャと呼ばれます。マルチステージ(MASH スタイル)アーキテクチャは、本質的に安定性の高い低次ループの組み合わせを通じて、安定した高次 Σ-Δ 変調器の設計を可能にします。
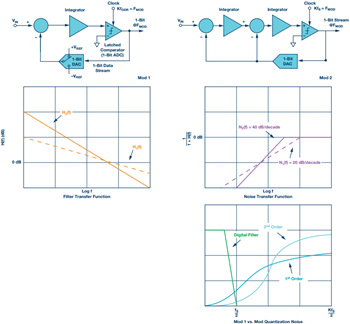
図 6. Mod 1 および Mod 2 のブロック構成、およびフィルタ伝達関数とノイズ伝達関数のプロット比較。




















