Design Note 214: Selecting Op Amps for Precision 16-Bit DAC
The LTC1597 16-bit current output DAC offers a new level of accuracy and cost efficiency. It has exceptionally high accuracy and low drift: ±1LSB (max) INL and DNL over temperature. It eliminates costly external resistors in bipolar applications because it includes tightly trimmed, on-chip 4-quadrant resistors. To help achieve the best circuit DC performance, this design note offers two sets of easy-to-use design equations for evaluating an op amp’s effects on the DAC’s accuracy in terms of INL, DNL, offset (unipolar), zero (bipolar), unipolar and bipolar gain errors. With this information, selecting an op amp that gives the accuracy you need in a unipolar or bipolar application is easy.
Figure 1 shows a unipolar application that combines the LTC1597 DAC and LT1468 fast settling op amp. The equations for evaluating the effects of the op amp on the DAC’s accuracy are shown in Table 1. Quick work on Table 1’s equations with a calculator gives the results shown in Table 2. These are the changes the op amp can cause to the INL, DNL, unipolar offset and gain error of the DAC. Note, all are substantially less than 1LSB. Thus, the LT1468 is an excellent choice.
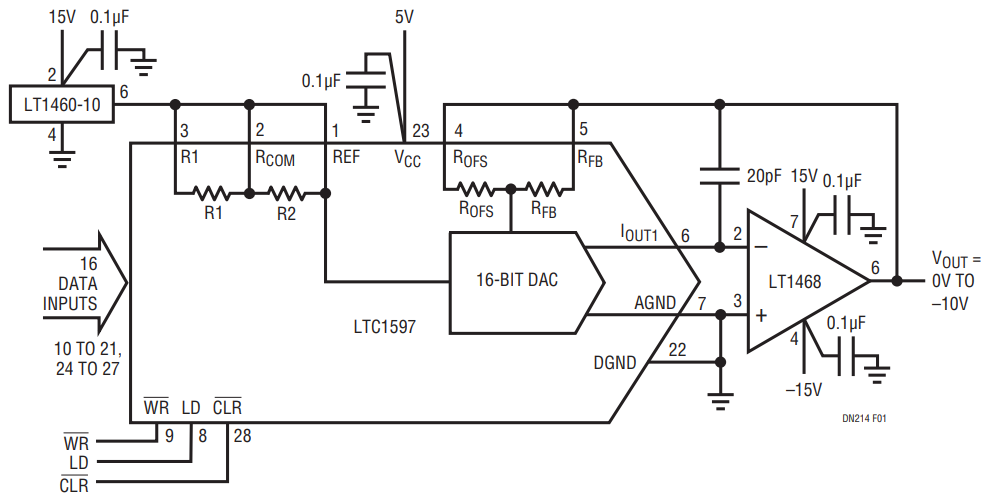
Figure 1. Unipolar VOUT DAC/Op Amp Circuit Swings 10VFS (0V to –10V) and Settles to 16 Bits in <2μs. For 0V to 10V Swings, the Reference Can Be Inverted with R1, R2 and Another Op Amp.
| Op Amp | INL (LSB) |
DNL (LSB) | Unipolar Offset (LSB) | Unipolar Gain Error (LSB) |
| VOS (mV) |
VOS • 1.2 • (10V/VREF) |
VOS • 0.3 • (10V/VREF) | VOS • 6.6 • (10V/VREF) |
VOS • 6.9 • (10V/VREF) |
| IB (nA) |
IB • 0.00055 • (10V/VREF) |
IB • 0.00015 • (10V/VREF) |
IB • 0.065 • (10V/VREF) |
0 |
| AVOL (V/V) | 10k/AVOL |
3k/AVOL | 0 | 131k/AVOL |
| LT1468 |
Typical | INL (LSB) |
DNL (LSB) |
Offset | Gain Error (LSB) |
| VOS (mV) |
0.03 | 0.036 |
0.009 |
0.2 | 0.21 |
| IB (nA) |
3 | 0.0017 |
0.0005 |
0.2 | 0 |
| AVOL (V/V) |
900k | 0.0011 |
0.0003 |
0 | 0.015 |
| Totals | 0.039 |
0.01 |
0.4 | 0.23 |
The LTC1597’s internal design is very insensitive to offset-induced INL and DNL changes. An op amp VOS as large as 0.5mV causes just 0.55LSB INL and 0.15LSB DNL in the output voltage for 10VFS. So, how does the LT1468 effect, for example, the DAC’s DNL? From Table 2, the LT1468 adds approximately 0.01LSB of additional DNL to the output. This, along with the LTC1597’s typical 0.2LSB DNL, give a total DAC/op amp DNL of just 0.21LSB (typ). This is well under the –1LSB needed to ensure monotonic operation.
Figure 2 shows a bipolar application that combines the LTC1597 and a dual LT1112 op amp. The equations for evaluating the effects of two amplifiers in bipolar operation are just as easy to use and are shown in Table 3. A quick application of Table 3’s equations gives the accuracy changes shown in Table 4. Again, each effect is substantially less than 1LSB. This shows that with proper op amp selection, the LTC1597’s excellent linearity and precision are not degraded even in bipolar applications.
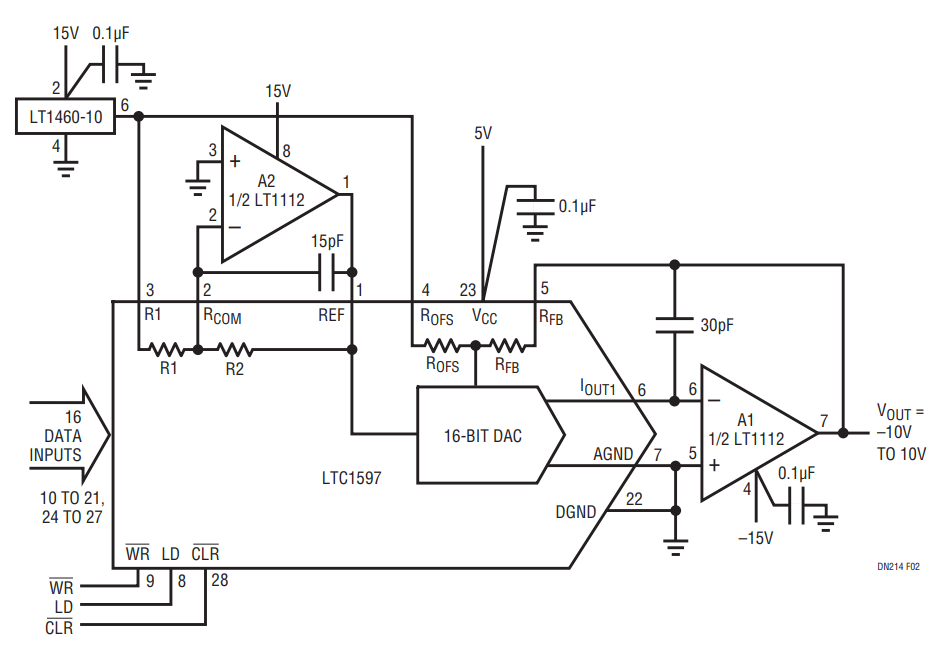
Figure 2. Bipolar Circuit Configuration for a 20V (VOUT = –10V to 10V) Output Swing.
| Op Amp | INL (LSB) |
DNL (LSB) | Bipolar Zero Error (LSB) | Bipolar Gain Error (LSB) |
| VOS1 (mV) |
VOS1 • 1.2 • (10V/VREF |
VOS1 • 0.3 • (10V/VREF) | VOS1 • 9.9 • (10V/VREF) | VOS1 • 6.9 • (10V/VREF) |
| IB1 (nA) |
IB1 • 0.00055 • (10V/VREF) |
IB1 • 0.00015 • (10V/VREF) | IB1 • 0.065 • (10V/VREF) |
0 |
| AVOL1 |
10k/AVOL |
3k/AVOL1 |
0 | 196k/AVOL1 |
| VOS2 (mV) |
0 | 0 | VOS2 • 6.7 • (10V/VREF) |
VOS2 • 13.2 • (10V/VREF) |
| IB2 (nA) | 0 | 0 | IB2 • 0.065 • (10V/VREF) | IB2 • 0.13 • (10V/VREF) |
| AVOL2 |
0 | 0 | 65k/AVOL2 | 131k/AVOL2 |
The totals in Tables 2 and 4 are algebraic sums of the absolute values, producing a worst-case error.
| LT1112 |
Typical | INL (LSB) | DNL (LSB) | Bipolar Zero Error (LSB) | Bipolar Gain Error (LSB) |
| VOS1 (mV) |
0.02 | 0.024 | 0.006 | 0.198 |
0.138 |
| IB1 (nA) |
0.07 | 0.00004 | 0.00001 |
0.0046 | 0 |
| AVOL1 |
500k | 0.002 | 0.0006 | 0 | 0.039 |
| VOS2 (mV) |
0.02 | 0 | 0 | 0.134 | 0.264 |
| IB2 (nA) | 0.07 | 0 | 0 | 0.0046 |
0.009 |
| AVOL2 | 500k | 0 | 0 | 0.013 | 0.026 |
| Totals | 0.026 | 0.007 | 0.354 | 0.476 |
While not directly addressed by the simple equations in Tables 1 and 3, temperature effects can be handled just as easily for unipolar and bipolar applications. First, consult an op amp’s data sheet to fi nd the worst-case VOS and IB over temperature. Then, plug these numbers in the VOS and IB equations from Table 1 or Table 3 and calculate the temperature induced effects.
