AN-1483: Harmonic Analysis Using the ADE9000
Introduction
Traditionally, harmonic analysis requires complex computations and processing. Harmonic analysis goes to an order of processing data in which a fixed analog-to-digital converter (ADC) sampling rate is used, then a window is applied into the data to account for the fact that the data is not sampled coherently. Lastly, a Fourier transform is performed, which can be difficult, because the number of samples of the data is not an exact amount of 2n integral numbers.
The ADE9000 metering IC is capable of performing the desired Fourier transform coherently or noncoherently using the waveform buffer application. Typically, this waveform buffer samples an amount of data and gives a set of values for a Fourier transform process. The output generated contains the fundamental signal plus all harmonics.
Another concern in harmonic analysis is that the signal being measured in the ADE9000 passes digital filtering, and the gain varies over frequency, thus attenuating the measurements at higher frequencies more noticeable beyond 500 Hz. Proper gain compensation factors must be introduced in measuring those frequencies affected by this process.
This application note discusses the ways of performing harmonic analysis and the gain compensation analysis using the EVAL-ADE9000EBZ evaluation board.
Coherent vs. Noncoherent Sampling
To obtain the fundamental and harmonic contents of the signal after the transformation process, it is essential to sample the signal in a way that it gives a perfectly generated output in root mean squared (rms) of the energy contents of each frequency.
Noncoherent sampling in the ADE9000 uses the waveform buffer to read enough samples for a fast Fourier transform (FFT). The timing clock and the size of the sample set is the main concern for noncoherent sampling. The energy content is concentrated at a single frequency if proper amounts of samples are generated for an FFT. It can be obtained by using an external clock, probably operating at the same timing with the generated signal and the input clock of the ADE9000. The requirement is also to generate a sample set that ends with the same exact point in the waveform where sampling starts. By doing this, each content of the signal is concentrated only to one specific point, thus measuring the rms values accurately.
Figure 1 shows an FFT response if noncoherent sampling is performed without taking into consideration the timing and the integral number of line periods. However, Figure 2 shows that when sampling starts and ends at the exact line period together with the clock sync, the content of the signal is concentrated on its specific frequency.

Figure 1. Response of a Third Harmonic of a Noncoherent Sampling Without Integral Number of Periods Using the ADE9000, NI PXI 4461 Signal Generator, and EVAL-ADE9000EBZ.

Figure 2. Third Harmonic of a 50 Hz Signal Noncoherent Sampling with Integral Number of Periods Using ADE9000, NI PXI 4461 Signal Generator, and EVAL-ADE9000EBZ.
The ADE9000 simplifies noncoherent signal processing by constantly tracking the power line frequency and using this information to resample the data to provide 128 points of data per power line, thus making the sampling coherent.
Coherent sampling also uses the waveform buffer and performs resampling of the original set of values. Each set contains 128 (128 × 4 maximum) interpolated samples providing one complete line cycle, which makes the number of samples an integral number of 2n power, thus making Fourier transform easy to compute. Interpolation introduces small errors that increase with the range of the harmonic (see Figure 3).

Figure 3. Response (in dB) of a Fundamental and Fifth Harmonic on Current Channel B Using 128 Samples/Line Cycle.
This application note discusses harmonic analysis using both noncoherent and coherent sampling modes.
Measuring Fundamental and Harmonic Contents
In performing harmonic analysis in the ADE9000, an FFT can be performed using a microcontroller or any software capable of performing signal processing (like LabVIEW®). Before measurement, a precalibration must be done using the ADE9000 Calibration Tool.
Harmonic Analysis using Noncoherent Sampling
The main register for measuring the harmonic content of the signal is the waveform buffer register.
Configure the register WFB_CFG with the following operations to control it in the desired waveform buffer setting to perform a noncoherent sampling mode. Make sure that the chip is precalibrated and working with the digital signal processor (DSP) on. See the ADE9000 Technical Reference Manual.
To set the waveform buffer, perform the following procedure:
- Write 0x03F8 to WFB_CFB (Address 0x4A0) to configure the waveform.
- Write 0'0b0 to WF_IN_EN (Bit 12) to disable waveform in neutral channel to be read through the serial peripheral interface (SPI).
- Write 0'b11 to WF_SRC (Bits[9:8]) to enable current and voltage channel waveform samples processed at 8 kSPS by the DSP.
- Write 0'b11 to WF_MODE (Bits[7:6]) to enable continuous fill on the buffer. See the ADE9000 Technical Reference Manual for more information on continuous filling mode.
- Write 0'b1 to WF_CAP_SEL (Bit 5) to enable the fixed data rate sampling (noncoherent).
- Write 0'b1 to WF_CAP_EN (Bit 4) to start waveform capturer.
- Write 0'b0000 for all channels to BURST_CHAN (Bits[3.0]) to select channels. See the ADE9000 data sheet for other channels.
Figure 4 shows the different sources of the waveform buffer. Waveform samples presented in this application note are captured from the output of the DSP core at a rate of 8 kSPS. It is recommended that the BURST_CHAN bits be 0ʹb0000 to access all channels.

Figure 4. Resampling Mode and Waveform Buffer Source.

Figure 5. Continuous Mode and Ping Pong Routine for Waveform Buffer.
By setting WFB_PG_IRQEN in continuous sampling, an interrupt sets at Page 7 and Page 15, dividing the waveform buffer into two major buffers and creating a ping pong buffer. After Page 0 to Page 7 are full, an interrupt enables, and a microcontroller and a PC can read the values on those pages, while the signal is continuously sampled on the remaining Page 8 to Page 15. After Page 8 to Page 15 are full, an interrupt enables again, reading the values stored on the pages while signal is sampled again on Page 0 to Page 7. Through this ping pong routine, no part of the wave is lost in continuous sampling. The WFB_LAST_PAGE bits on the WFB_ TRIG_STAT register help determine which part of the buffer is filled to start the read routine on that part of the buffer.
To execute this process, take the following steps:
- Write 0x20000 to MASK0 (Address 0x405) to enable the page full interrupt.
- Write 0x8080 to WFB_PG_IRQWN (Address 0x4A1) to set the interrupt at Page 7 and Page 15.
Figure 6 summarizes the procedure on how to operate the noncoherent sampling mode using the waveform buffer.

Figure 6. Implementing the Noncoherent Mode Resampling.
The complete list of registers for the waveform buffer is available in the ADE9000 data sheet.
The expected values to be measured after an FFT process can be computed using the following equations:
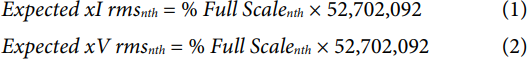
where % Full Scalen this the percentage of the full-scale content of the signal.
Input defined in this application note are expressed in terms of percentages of the full-scale ADC output in codes.
To compute for the expected total rms values, use the following equation:
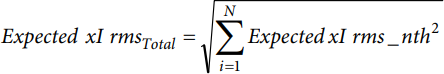
This application note provides an actual measurement of the rms of a fundamental 50 Hz with a harmonic content following the IEC62053-21 with the test conditions found in Table 1.
| Test Condition | Value |
| Fundamental Current | 0.5 IMAX |
| Fundamental Voltage | UN |
| Fundamental Power Factor | 1 |
| Content of the Fifth Harmonic Voltage | 10% of UN |
| Content of the Fifth Harmonic Current | 40% (0.5 IMAX) |
IMAX was selected to be used as the full-scale 1 V.
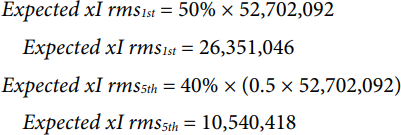
UN was selected to be 20% of the full-scale code.
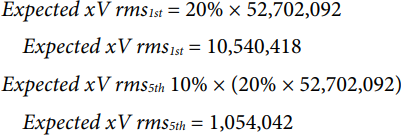
To compute for the expected total I rms and V rms, take the rms of the individual values:
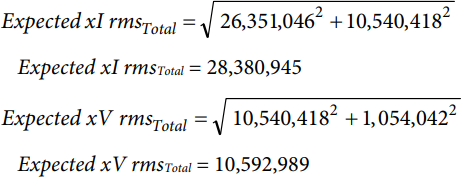
An actual test for noncoherent mode is performed using the EVAL-ADE9000EBZ evaluation board. After the waveform sampling, the microcontroller performs an FFT in which each harmonic content is extracted. For this case, the input is a fundamental signal with a fifth harmonic same as above. For this experiment, LabVIEW has been used as a tool to calculate the FFT and output the harmonic contents of the signal. The rms values of each (fundamental and harmonics) is measured after an FFT for further analysis. The results are shown in Table 2 and Table 3.
| Input | Expected Value | Measured FFT | Percent Error |
| Fundamental | 26,351,046 | 26,347,599 | 0.0131% |
| Fifth Harmonic | 10,540,418 | 10,532,242 | 0.0776% |
| Input | Expected Value | Measured FFT | Percent Error |
| Fundamental | 10,540,418 | 10,547,428 | 0.0665% |
| Fifth Harmonic | 1,054,042 | 1,054,775 | 0.0695% |
The reading from the AIFRMS register during this experiment is 26347436, which is 0.014% off of the expected value, and the reading from the AVFRMS register is 10,548,545, which is 0.0771% off of the expected value.
Using the rms values after the FFT, the total rms for voltage and current were calculated.
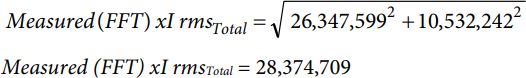
The same calculation is used for the voltage.
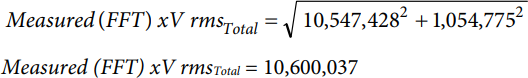
Table 4 and Table 5 describe the comparison between the expected values of the total rms, the FFT measured total rms, and the reading on the register.
| Input | Expected Value | Measured FFT | Percent Error |
| xI rmsTotal | 28,380,945 | 28,374,709 | 0.0220% |
| xV rmsTotal | 10,592,989 | 10,600,037 | 0.0665% |
| Input | Expected Value | Register Reading AI rms/AV rms | Percent Error |
| xI rmsTotal | 28,380,945 | 28,374,967 | 0.0211% |
| xV rmsTotal | 10,592,989 | 10,599,835 | 0.0646% |
The current total harmonic distortion can also be calculated using the following equation:
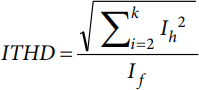
Calculate the expected ITHD using the following equation:
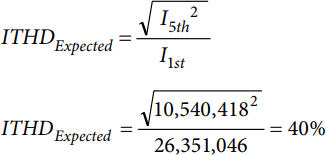
ITHD using the measured values from FFT can be figured by the following equation:
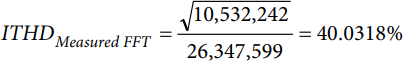
The AITHD register can also be read for comparison. The total harmonic distortion (THD) discussion is further elaborated on in the ADE9000 data sheet.
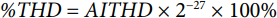
With the same input, the measured value on AITHD is 0x33327DC and using the formula, the %THD is 39.9978%.
| Expected ITHD | Computed ITHD Based on Measured (FFT) | THD Based on AITHD Register |
| 40% | 40.0318% | 39.9978% |
The same procedure is repeated in the voltage channel, and the data in Table 7 was obtained.
| Expected VTHD | Computed VTHD Based on Measured (FFT) | THD Based on AVTHD Register |
| 10% | 10.0147% | 10.0012% |
Harmonic Analysis using Coherent Sampling
There are initial configurations to be considered before performing harmonic analysis using coherent sampling. The same register, WFB_CFG, is to be configured with the same settings as with the noncoherent sampling except for the WF_CAP_SEL bit. This bit must be set to 0 to configure the waveform buffer in resampled data mode. The resampled data mode has a full scale of 18,196. The following equation can be used to obtain the expected values converted in rms:
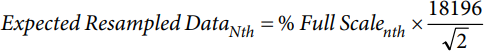
Using the same input as the noncoherent mode and the equations for computing current and voltage resampled data and THD, a new set of expected values were obtained and compared to the measured value upon performing an FFT.
The ITHD and VTHD are also computed based on expected resampled values, measured values after the FFT, and on the AITHD and AVTHD registers.
| Content | Percentage Full Scale | Full Scale | Expected Value | Measured (FFT) | Percentage Error |
| Fundamental | 50% | 18,196 | 6433 | 6433 | 0.2493% |
| Fifth Harmonic | 20% | 18,196 | 2573 | 2565 | 0.3319% |
| Content | Percentage Full Scale | Full Scale | Expected Value | Measured (FFT) | Percentage Error |
| Fundamental | 20% | 18,196 | 2573 | 2570 | 0.1167% |
| Fifth Harmonic | 2% | 18,196 | 257 | 258 | 0.3876% |
| Parameter | Expected THD (Based on Resampled Values) | Computed THD Based on Measured (FFT) | Reading on AxTHD Register |
| AITHD | 39.9969% | 40.0499% | 39.9978% |
| AVTHD | 9.9883% | 10.0585% | 10.0012% |
Harmonic Gain Response of the ADE9000 Digital Filter
The signal that passes through the DSP of the ADE9000 is processed through digital filtering, which has a sinc4 filter with 32 KSPS output data rate followed by a low-pass filter (LPF). Due to the digital filtering, the gain of the samples in the waveform buffer varies over frequency, thus attenuating the measurements at higher frequencies. Figure 7 shows the gain performance of the digital filter.

Figure 7. % Gain Error of ADE9000 Sinc4 + LPF Response.
Table 11 and Table 12 summarize the whole performance of the digital filter in percent gain error and the gain compensation factor of each harmonic at 50 Hz and 60 Hz.
| Harmonic No. | Frequency | Attenuation Factor | Gain Compensation Factor |
| 1 | 50 | 1.00000 | 1.00000 |
| 2 | 100 | 0.99997 | 1.00003 |
| 3 | 150 | 0.99992 | 1.00008 |
| 4 | 200 | 0.99985 | 1.00015 |
| 5 | 250 | 0.99976 | 1.00024 |
| 6 | 300 | 0.99964 | 1.00036 |
| 7 | 350 | 0.99948 | 1.00052 |
| 8 | 400 | 0.99930 | 1.00070 |
| 9 | 450 | 0.99908 | 1.00092 |
| 10 | 500 | 0.99882 | 1.00118 |
| 11 | 550 | 0.99851 | 1.00149 |
| 12 | 600 | 0.99816 | 1.00184 |
| 13 | 650 | 0.99777 | 1.00223 |
| 14 | 700 | 0.99732 | 1.00269 |
| 15 | 750 | 0.99683 | 1.00318 |
| 16 | 800 | 0.99629 | 1.00372 |
| 17 | 850 | 0.99571 | 1.00431 |
| 18 | 900 | 0.99508 | 1.00494 |
| 19 | 950 | 0.99441 | 1.00562 |
| 20 | 1000 | 0.99370 | 1.00634 |
| 21 | 1050 | 0.99297 | 1.00708 |
| 22 | 1100 | 0.99220 | 1.00786 |
| 23 | 1150 | 0.99141 | 1.00866 |
| 24 | 1200 | 0.99060 | 1.00949 |
| 25 | 1250 | 0.98977 | 1.01034 |
| 26 | 1300 | 0.98893 | 1.01119 |
| 27 | 1350 | 0.98808 | 1.01206 |
| 28 | 1400 | 0.98723 | 1.01294 |
| 29 | 1450 | 0.98636 | 1.01383 |
| 30 | 1500 | 0.98547 | 1.01474 |
| 31 | 1550 | 0.98457 | 1.01567 |
| 32 | 1600 | 0.98365 | 1.01662 |
| 33 | 1650 | 0.98270 | 1.01760 |
| 34 | 1700 | 0.98172 | 1.01862 |
| 35 | 1750 | 0.98069 | 1.01969 |
| 36 | 1800 | 0.97962 | 1.02080 |
| 37 | 1850 | 0.97849 | 1.02198 |
| 38 | 1900 | 0.97730 | 1.02323 |
| 39 | 1950 | 0.97605 | 1.02454 |
| 40 | 2000 | 0.97475 | 1.02590 |
| 41 | 2050 | 0.97340 | 1.02733 |
| 42 | 2100 | 0.97200 | 1.02881 |
| 43 | 2150 | 0.97058 | 1.03031 |
| 44 | 2200 | 0.96914 | 1.03184 |
| 45 | 2250 | 0.96770 | 1.03338 |
| 46 | 2300 | 0.96627 | 1.03491 |
| 47 | 2350 | 0.96486 | 1.03642 |
| 48 | 2400 | 0.96347 | 1.03792 |
| 49 | 2450 | 0.96209 | 1.03940 |
| 50 | 2500 | 0.96069 | 1.04092 |
| 51 | 2550 | 0.95925 | 1.04248 |
| 52 | 2600 | 0.95772 | 1.04415 |
| 53 | 2650 | 0.95608 | 1.04594 |
| 54 | 2700 | 0.95431 | 1.04788 |
| 55 | 2750 | 0.95244 | 1.04993 |
| 56 | 2800 | 0.95056 | 1.05201 |
| 57 | 2850 | 0.94878 | 1.05399 |
| 58 | 2900 | 0.94722 | 1.05572 |
| 59 | 2950 | 0.94572 | 1.05740 |
| 60 | 3000 | 0.94335 | 1.06005 |
| 61 | 3050 | 0.93736 | 1.06683 |
| 62 | 3100 | 0.92128 | 1.08545 |
| 63 | 3150 | 0.88338 | 1.13202 |
| Harmonic No. | Frequency | Attenuation Factor | Gain Compensation Factor |
| 1 | 60 | 1.00000 | 1.00000 |
| 2 | 120 | 0.99996 | 1.00004 |
| 3 | 180 | 0.99989 | 1.00011 |
| 4 | 240 | 0.99978 | 1.00022 |
| 5 | 300 | 0.99964 | 1.00036 |
| 6 | 360 | 0.99945 | 1.00055 |
| 7 | 420 | 0.99922 | 1.00078 |
| 8 | 480 | 0.99893 | 1.00107 |
| 9 | 540 | 0.99858 | 1.00142 |
| 10 | 600 | 0.99817 | 1.00183 |
| 11 | 660 | 0.99769 | 1.00232 |
| 12 | 720 | 0.99714 | 1.00287 |
| 13 | 780 | 0.99652 | 1.00349 |
| 14 | 840 | 0.99583 | 1.00419 |
| 15 | 900 | 0.99508 | 1.00494 |
| 16 | 960 | 0.99428 | 1.00575 |
| 17 | 1020 | 0.99342 | 1.00662 |
| 18 | 1080 | 0.99251 | 1.00755 |
| 19 | 1140 | 0.99157 | 1.00850 |
| 20 | 1200 | 0.99060 | 1.00949 |
| 21 | 1260 | 0.98961 | 1.01050 |
| 22 | 1320 | 0.98860 | 1.01153 |
| 23 | 1380 | 0.98757 | 1.01259 |
| 24 | 1440 | 0.98653 | 1.01365 |
| 25 | 1500 | 0.98548 | 1.01473 |
| 26 | 1560 | 0.98439 | 1.01586 |
| 27 | 1620 | 0.98328 | 1.01700 |
| 28 | 1680 | 0.98212 | 1.01821 |
| 29 | 1740 | 0.98090 | 1.01947 |
| 30 | 1800 | 0.97962 | 1.02080 |
| 31 | 1860 | 0.97826 | 1.02222 |
| 32 | 1920 | 0.97681 | 1.02374 |
| 33 | 1980 | 0.97528 | 1.02535 |
| 34 | 2040 | 0.97368 | 1.02703 |
| 35 | 2100 | 0.97201 | 1.02880 |
| 36 | 2160 | 0.97029 | 1.03062 |
| 37 | 2220 | 0.96857 | 1.03245 |
| 38 | 2280 | 0.96684 | 1.03430 |
| 39 | 2340 | 0.96514 | 1.03612 |
| 40 | 2400 | 0.96347 | 1.03792 |
| 41 | 2460 | 0.96181 | 1.03971 |
| 42 | 2520 | 0.96013 | 1.04153 |
| 43 | 2580 | 0.95835 | 1.04346 |
| 44 | 2640 | 0.95643 | 1.04555 |
| 45 | 2700 | 0.95432 | 1.04787 |
| 46 | 2760 | 0.95207 | 1.05034 |
| 47 | 2820 | 0.94983 | 1.05282 |
| 48 | 2880 | 0.94782 | 1.05505 |
| 49 | 2940 | 0.94604 | 1.05704 |
| 50 | 3000 | 0.94336 | 1.06004 |
| 51 | 3060 | 0.93525 | 1.06923 |
| 52 | 3120 | 0.90957 | 1.09942 |
| 53 | 3180 | 0.84404 | 1.18478 |
| 54 | 3240 | 0.72078 | 1.38739 |
| 55 | 3300 | 0.55810 | 1.79179 |
Gain Response of Antialias Filter
The external resistor capacitor (RC) that prevents aliasing has a response that affects the signals at frequencies higher than 2000 Hz.

Figure 8. ADE9000 Antialias Filter.
The recommended values of 1 kΩ and 22 nF theoretically follow the transfer function that provide the gain response expressed in Figure 9.
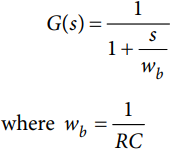

Figure 9. ADE9000 Antialias Filter Response (1 kΩ, 22 nF).
The combined effect of the sinc4 and LPF digital filter and the external antialias filter create a significant gain error to high frequencies. Table 13 and Table 14 the whole performance of the digital filters including the recommended antialias filter with proper gain compensation factors for each harmonic at 50 Hz and 60 Hz.
| Harmonic No. | Frequency | Attenuation Factor | Gain Compensation Factor |
| 1 | 50 | 1.00000 | 1.00000 |
| 2 | 100 | 0.99993 | 1.00007 |
| 3 | 150 | 0.99981 | 1.00019 |
| 4 | 200 | 0.99964 | 1.00036 |
| 5 | 250 | 0.99943 | 1.00057 |
| 6 | 300 | 0.99917 | 1.00083 |
| 7 | 350 | 0.99886 | 1.00114 |
| 8 | 400 | 0.99850 | 1.00150 |
| 9 | 450 | 0.99809 | 1.00191 |
| 10 | 500 | 0.99764 | 1.00237 |
| 11 | 550 | 0.99715 | 1.00286 |
| 12 | 600 | 0.99660 | 1.00341 |
| 13 | 650 | 0.99601 | 1.00401 |
| 14 | 700 | 0.99538 | 1.00464 |
| 15 | 750 | 0.99469 | 1.00534 |
| 16 | 800 | 0.99396 | 1.00608 |
| 17 | 850 | 0.99319 | 1.00686 |
| 18 | 900 | 0.99237 | 1.00769 |
| 19 | 950 | 0.99151 | 1.00856 |
| 20 | 1000 | 0.99060 | 1.00949 |
| 21 | 1050 | 0.98965 | 1.01046 |
| 22 | 1100 | 0.98866 | 1.01147 |
| 23 | 1150 | 0.98762 | 1.01254 |
| 24 | 1200 | 0.98654 | 1.01364 |
| 25 | 1250 | 0.98542 | 1.01480 |
| 26 | 1300 | 0.98426 | 1.01599 |
| 27 | 1350 | 0.98305 | 1.01724 |
| 28 | 1400 | 0.98181 | 1.01853 |
| 29 | 1450 | 0.98052 | 1.01987 |
| 30 | 1500 | 0.97920 | 1.02124 |
| 31 | 1550 | 0.97783 | 1.02267 |
| 32 | 1600 | 0.97643 | 1.02414 |
| 33 | 1650 | 0.97499 | 1.02565 |
| 34 | 1700 | 0.97351 | 1.02721 |
| 35 | 1750 | 0.97199 | 1.02882 |
| 36 | 1800 | 0.97044 | 1.03046 |
| 37 | 1850 | 0.96885 | 1.03215 |
| 38 | 1900 | 0.96722 | 1.03389 |
| 39 | 1950 | 0.96556 | 1.03567 |
| 40 | 2000 | 0.96387 | 1.03748 |
| 41 | 2050 | 0.96214 | 1.03935 |
| 42 | 2100 | 0.96038 | 1.04125 |
| 43 | 2150 | 0.95859 | 1.04320 |
| 44 | 2200 | 0.95676 | 1.04519 |
| 45 | 2250 | 0.95490 | 1.04723 |
| 46 | 2300 | 0.95302 | 1.04930 |
| 47 | 2350 | 0.95110 | 1.05141 |
| 48 | 2400 | 0.94916 | 1.05356 |
| 49 | 2450 | 0.94718 | 1.05577 |
| 50 | 2500 | 0.94518 | 1.05800 |
| 51 | 2550 | 0.94315 | 1.06028 |
| 52 | 2600 | 0.94109 | 1.06260 |
| 53 | 2650 | 0.93901 | 1.06495 |
| 54 | 2700 | 0.93690 | 1.06735 |
| 55 | 2750 | 0.93476 | 1.06979 |
| 56 | 2800 | 0.93261 | 1.07226 |
| 57 | 2850 | 0.93043 | 1.07477 |
| 58 | 2900 | 0.92822 | 1.07733 |
| 59 | 2950 | 0.92599 | 1.07993 |
| 60 | 3000 | 0.92375 | 1.08254 |
| 61 | 3050 | 0.92148 | 1.08521 |
| 62 | 3100 | 0.91919 | 1.08791 |
| 63 | 3150 | 0.91688 | 1.09066 |
| Harmonic No. | Frequency | Attenuation Factor | Gain Compensation Factor |
| 1 | 60 | 1.00000 | 1.00000 |
| 2 | 120 | 0.99990 | 1.00010 |
| 3 | 180 | 0.99972 | 1.00028 |
| 4 | 240 | 0.99948 | 1.00052 |
| 5 | 300 | 0.99918 | 1.00082 |
| 6 | 360 | 0.99980 | 1.00120 |
| 7 | 420 | 0.99835 | 1.00165 |
| 8 | 480 | 0.99784 | 1.00216 |
| 9 | 540 | 0.99726 | 1.00275 |
| 10 | 600 | 0.99661 | 1.00340 |
| 11 | 660 | 0.99590 | 1.00412 |
| 12 | 720 | 0.99512 | 1.00490 |
| 13 | 780 | 0.99427 | 1.00576 |
| 14 | 840 | 0.99336 | 1.00668 |
| 15 | 900 | 0.99238 | 1.00768 |
| 16 | 960 | 0.99134 | 1.00874 |
| 17 | 1020 | 0.99024 | 1.00986 |
| 18 | 1080 | 0.98907 | 1.01105 |
| 19 | 1140 | 0.98784 | 1.01231 |
| 20 | 1200 | 0.98655 | 1.01363 |
| 21 | 1260 | 0.98520 | 1.01502 |
| 22 | 1320 | 0.98379 | 1.01648 |
| 23 | 1380 | 0.98232 | 1.01800 |
| 24 | 1440 | 0.98079 | 1.01959 |
| 25 | 1500 | 0.97921 | 1.02123 |
| 26 | 1560 | 0.97756 | 1.02296 |
| 27 | 1620 | 0.97587 | 1.02473 |
| 28 | 1680 | 0.97411 | 1.02658 |
| 29 | 1740 | 0.97231 | 1.02848 |
| 30 | 1800 | 0.97045 | 1.03045 |
| 31 | 1860 | 0.96853 | 1.03249 |
| 32 | 1920 | 0.96657 | 1.03459 |
| 33 | 1980 | 0.96456 | 1.03674 |
| 34 | 2040 | 0.96250 | 1.03896 |
| 35 | 2100 | 0.96039 | 1.04124 |
| 36 | 2160 | 0.95823 | 1.04359 |
| 37 | 2220 | 0.95603 | 1.04599 |
| 38 | 2280 | 0.95379 | 1.04845 |
| 39 | 2340 | 0.95150 | 1.05097 |
| 40 | 2400 | 0.94917 | 1.05355 |
| 41 | 2460 | 0.94679 | 1.05620 |
| 42 | 2520 | 0.94438 | 1.05890 |
| 43 | 2580 | 0.94193 | 1.06165 |
| 44 | 2640 | 0.93944 | 1.06446 |
| 45 | 2700 | 0.93691 | 1.06734 |
| 46 | 2760 | 0.93434 | 1.07027 |
| 47 | 2820 | 0.93175 | 1.07325 |
| 48 | 2880 | 0.92912 | 1.07629 |
| 49 | 2940 | 0.92645 | 1.07939 |
| 50 | 3000 | 0.92376 | 1.08253 |
| 51 | 3060 | 0.92103 | 1.08574 |
| 52 | 3120 | 0.91827 | 1.08900 |
| 53 | 3180 | 0.91549 | 1.09231 |
| 54 | 3240 | 0.91268 | 1.09567 |
| 55 | 3300 | 0.90984 | 1.09909 |
A full harmonic analysis is performed on Current Channel A at 50 Hz to verify the combined effect of the antialias filter of the EVAL-ADE9000EBZ and the sinc4 + LPF. The correction factors are introduced to the measurements to compensate the attenuation introduced by the sinc4 + LPF plus antialias filter. The results are shown in Table 15 and Table 16.
| Harmonic No. | Frequency (50 Hz) | Combined Attenuation | Combined Gain Compensation Factor |
| 1 | 50 | 1 | 1.00000 |
| 2 | 100 | 0.9999 | 1.00010 |
| 3 | 150 | 0.999723 | 1.00027 |
| 4 | 200 | 0.999494 | 1.00051 |
| 5 | 250 | 0.999184 | 1.00082 |
| 6 | 300 | 0.999801 | 1.00120 |
| 7 | 350 | 0.99834 | 1.00166 |
| 8 | 400 | 0.997798 | 1.00221 |
| 9 | 450 | 0.997173 | 1.00284 |
| 10 | 500 | 0.996462 | 1.00355 |
| 11 | 550 | 0.995662 | 1.00436 |
| 12 | 600 | 0.994771 | 1.00526 |
| 13 | 650 | 0.993788 | 1.00625 |
| 14 | 700 | 0.992712 | 1.00734 |
| 15 | 750 | 0.991542 | 1.00853 |
| 16 | 800 | 0.990281 | 1.00981 |
| 17 | 850 | 0.98893 | 1.01119 |
| 18 | 900 | 0.987491 | 1.01267 |
| 19 | 950 | 0.985969 | 1.01423 |
| 20 | 1000 | 0.984368 | 1.01588 |
| 21 | 1050 | 0.982692 | 1.01761 |
| 22 | 1100 | 0.980947 | 1.01942 |
| 23 | 1150 | 0.979137 | 1.02131 |
| 24 | 1200 | 0.977267 | 1.02326 |
| 25 | 1250 | 0.975343 | 1.02528 |
| 26 | 1300 | 0.973366 | 1.02736 |
| 27 | 1350 | 0.97134 | 1.02951 |
| 28 | 1400 | 0.969266 | 1.03171 |
| 29 | 1450 | 0.967143 | 1.03397 |
| 30 | 1500 | 0.964971 | 1.03630 |
| 31 | 1550 | 0.962747 | 1.03869 |
| 32 | 1600 | 0.960465 | 1.04116 |
| 33 | 1650 | 0.958121 | 1.04371 |
| 34 | 1700 | 0.955708 | 1.04634 |
| 35 | 1750 | 0.953221 | 1.04907 |
| 36 | 1800 | 0.950655 | 1.05191 |
| 37 | 1850 | 0.948003 | 1.05485 |
| 38 | 1900 | 0.945265 | 1.05790 |
| 39 | 1950 | 0.94244 | 1.06108 |
| 40 | 2000 | 0.939531 | 1.06436 |
| 41 | 2050 | 0.936545 | 1.06775 |
| 42 | 2100 | 0.933491 | 1.07125 |
| 43 | 2150 | 0.930383 | 1.07483 |
| 44 | 2200 | 0.927234 | 1.07848 |
| 45 | 2250 | 0.92406 | 1.08218 |
| 46 | 2300 | 0.920872 | 1.08593 |
| 47 | 2350 | 0.917679 | 1.08971 |
| 48 | 2400 | 0.914482 | 1.09352 |
| 49 | 2450 | 0.91127 | 1.09737 |
| 50 | 2500 | 0.908024 | 1.10129 |
| 51 | 2550 | 0.904714 | 1.10532 |
| 52 | 2600 | 0.901305 | 1.10950 |
| 53 | 2650 | 0.897768 | 1.11387 |
| 54 | 2700 | 0.894094 | 1.11845 |
| 55 | 2750 | 0.890311 | 1.12320 |
| 56 | 2800 | 0.886497 | 1.12804 |
| 57 | 2850 | 0.882771 | 1.13280 |
| 58 | 2900 | 0.879228 | 1.13736 |
| 59 | 2950 | 0.875728 | 1.14191 |
| 60 | 3000 | 0.87142 | 1.14755 |
| 61 | 3050 | 0.863753 | 1.15774 |
| 62 | 3100 | 0.84683 | 1.18087 |
| 63 | 3150 | 0.809953 | 1.23464 |
| Harmonic No. | Frequency (60 Hz) | Combined Attenuation | Combined Gain Compensation Factor |
| 1 | 60 | 1 | 1.00000 |
| 2 | 120 | 0.999855 | 1.00015 |
| 3 | 180 | 0.999612 | 1.00039 |
| 4 | 240 | 0.999267 | 1.00073 |
| 5 | 300 | 0.998815 | 1.00119 |
| 6 | 360 | 0.998252 | 1.00175 |
| 7 | 420 | 0.997573 | 1.00243 |
| 8 | 480 | 0.996772 | 1.00324 |
| 9 | 540 | 0.995844 | 1.00417 |
| 10 | 600 | 0.994786 | 1.00524 |
| 11 | 660 | 0.993595 | 1.00645 |
| 12 | 720 | 0.99227 | 1.00779 |
| 13 | 780 | 0.990811 | 1.00927 |
| 14 | 840 | 0.989222 | 1.01090 |
| 15 | 900 | 0.987506 | 1.01265 |
| 16 | 960 | 0.98567 | 1.01454 |
| 17 | 1020 | 0.983721 | 1.01655 |
| 18 | 1080 | 0.981667 | 1.01868 |
| 19 | 1140 | 0.979518 | 1.02091 |
| 20 | 1200 | 0.977282 | 1.02325 |
| 21 | 1260 | 0.974966 | 1.02568 |
| 22 | 1320 | 0.972575 | 1.02820 |
| 23 | 1380 | 0.970115 | 1.03081 |
| 24 | 1440 | 0.967586 | 1.03350 |
| 25 | 1500 | 0.964985 | 1.03629 |
| 26 | 1560 | 0.962309 | 1.03917 |
| 27 | 1620 | 0.959549 | 1.04216 |
| 28 | 1680 | 0.956696 | 1.04526 |
| 29 | 1740 | 0.953739 | 1.04850 |
| 30 | 1800 | 0.950669 | 1.05189 |
| 31 | 1860 | 0.947477 | 1.05543 |
| 32 | 1920 | 0.944159 | 1.05914 |
| 33 | 1980 | 0.940718 | 1.06302 |
| 34 | 2040 | 0.937162 | 1.06705 |
| 35 | 2100 | 0.933505 | 1.07123 |
| 36 | 2160 | 0.929769 | 1.07554 |
| 37 | 2220 | 0.92598 | 1.07994 |
| 38 | 2280 | 0.922162 | 1.08441 |
| 39 | 2340 | 0.918332 | 1.08893 |
| 40 | 2400 | 0.914495 | 1.09350 |
| 41 | 2460 | 0.910638 | 1.09813 |
| 42 | 2520 | 0.906723 | 1.10287 |
| 43 | 2580 | 0.902696 | 1.10779 |
| 44 | 2640 | 0.8985 | 1.11297 |
| 45 | 2700 | 0.894107 | 1.11843 |
| 46 | 2760 | 0.88956 | 1.12415 |
| 47 | 2820 | 0.885002 | 1.12994 |
| 48 | 2880 | 0.880636 | 1.13554 |
| 49 | 2940 | 0.876462 | 1.14095 |
| 50 | 3000 | 0.871433 | 1.14754 |
| 51 | 3060 | 0.861391 | 1.16091 |
| 52 | 3120 | 0.835236 | 1.19727 |
| 53 | 3180 | 0.772715 | 1.29414 |
| 54 | 3240 | 0.65784 | 1.52013 |
| 55 | N/A | N/A | N/A |
| 56 | N/A | N/A | N/A |
| 57 | N/A | N/A | N/A |
| 58 | N/A | N/A | N/A |
| 59 | N/A | N/A | N/A |
| 60 | N/A | N/A | N/A |
| 61 | N/A | N/A | N/A |
| 62 | N/A | N/A | N/A |
| 63 | N/A | N/A | N/A |
| 1 N/A means not applicable. | |||

Figure 10. EVAL-ADE9000EBZ Current Channel A RMS Error vs. Frequency after correction (50% Full Scale, 50 Hz).
Measured Test Results using EVAL-ADE9000EBZ
A full harmonic analysis using the EVAL-ADE9000EBZ was performed on Channel IA using the noncoherent analysis with 50% full scale for both fundamental and harmonics. After the FFT, the gain errors listed in Table 17 were obtained and compared to the gain errors of the combined sinc4 + LPF + antialias listed in Table 15. The rms contents with the errors are corrected using the compensation factors listed in Table 13. The results are shown in Table 18.
| Harmonic No. | Frequency | Actual Measured Gain Error | Typical Combined Gain Error |
| 1 | 50 | 0% | 0% |
| 2 | 100 | 0.0085% | −0.010% |
| 3 | 150 | −0.0209% | −0.027% |
| 4 | 200 | −0.0482% | −0.051% |
| 5 | 250 | −0.0814% | −0.082% |
| 6 | 300 | −0.1234% | −0.120% |
| 7 | 350 | −0.1703% | −0.166% |
| 8 | 400 | −0.2278% | −0.220% |
| 9 | 450 | −0.2911% | −0.283% |
| 10 | 500 | −0.3654% | −0.354% |
| 11 | 550 | −0.4487% | −0.434% |
| 12 | 600 | −0.5392% | −0.523% |
| 13 | 650 | −0.6396% | −0.621% |
| 14 | 700 | −0.7508% | −0.729% |
| 15 | 750 | −0.8686% | −0.846% |
| 16 | 800 | −0.9991% | −0.972% |
| 17 | 850 | −1.1358% | −1.107% |
| 18 | 900 | −1.2837% | −1.251% |
| 19 | 950 | −1.4379% | −1.403% |
| 20 | 1000 | −1.6026% | −1.563% |
| 21 | 1050 | −1.7728% | −1.731% |
| 22 | 1100 | −1.9529% | −1.905% |
| 23 | 1150 | −2.1355% | −2.086% |
| 24 | 1200 | −2.3255% | −2.273% |
| 25 | 1250 | −2.5249% | −2.466% |
| 26 | 1300 | −2.7260% | −2.663% |
| 27 | 1350 | −2.9330% | −2.866% |
| 28 | 1400 | −3.1420% | −3.073% |
| 29 | 1450 | −3.3594% | −3.286% |
| 30 | 1500 | −3.5799% | −3.503% |
| 31 | 1550 | −3.8069% | −3.725% |
| 32 | 1600 | −4.0397% | −3.954% |
| 33 | 1650 | −4.2800% | −4.188% |
| 34 | 1700 | −4.5263% | −4.429% |
| 35 | 1750 | −4.7801% | −4.678% |
| 36 | 1800 | −5.0414% | −4.935% |
| 37 | 1850 | −5.3127% | −5.200% |
| 38 | 1900 | −5.5913% | −5.473% |
| 39 | 1950 | −5.8785% | −5.756% |
| 40 | 2000 | −6.1742% | −6.047% |
| 41 | 2050 | −6.4778% | −6.346% |
| 42 | 2100 | −6.7909% | −6.651% |
| 43 | 2150 | −7.1056% | −6.962% |
| 44 | 2200 | −7.4254% | −7.277% |
| 45 | 2250 | −7.7491% | −7.594% |
| 46 | 2300 | −8.0723% | −7.913% |
| 47 | 2350 | −8.3985% | −8.232% |
| 48 | 2400 | −8.7237% | −8.552% |
| 49 | 2450 | −9.0526% | −8.873% |
| 50 | 2500 | −9.3832% | −9.198% |
| 51 | 2550 | −9.7194% | −9.529% |
| 52 | 2600 | −10.0646% | −9.870% |
| 53 | 2650 | −10.4263% | −10.223% |
| 54 | 2700 | −10.7984% | −10.591% |
| 55 | 2750 | −11.1817% | −10.969% |
| 56 | 2800 | −11.5689% | −11.350% |
| 57 | 2850 | −11.9442% | −11.723% |
| 58 | 2900 | −12.3064% | −12.077% |
| 59 | 2950 | −12.6606% | −12.427% |
| 60 | 3000 | −13.0965% | −12.858% |
| 61 | 3050 | −13.8693% | −13.625% |
| 62 | 3100 | −15.5630% | −15.317% |
| 63 | 3150 | −19.2473% | −19.005% |
| Harmonic No. | Frequency | Harmonic Content in RMS | Gain Compensation Factor | Corrected Value | % Error |
| 1 | 50 | 26348904 | 1 | 26348903.6 | 0.00495% |
| 2 | 100 | 26337468 | 1.0001 | 26340102 | −0.02845% |
| 3 | 150 | 26343066 | 1.00027 | 26350178.2 | 0.00979% |
| 4 | 200 | 26323856 | 1.00051 | 26337280.9 | −0.03916% |
| 5 | 250 | 26313297 | 1.00082 | 26334873.5 | −0.04830% |
| 6 | 300 | 26304634 | 1.0012 | 26336200 | −0.04326% |
| 7 | 350 | 26292245 | 1.00166 | 26335890.2 | −0.04444% |
| 8 | 400 | 26277729 | 1.00221 | 26335802.3 | −0.04477% |
| 9 | 450 | 26260805 | 1.00284 | 26335386 | −0.04635% |
| 10 | 500 | 26241411 | 1.00355 | 26334567.7 | −0.04946% |
| 11 | 550 | 26220309 | 1.00436 | 26334629.8 | −0.04922% |
| 12 | 600 | 26196100 | 1.00526 | 26333891.6 | −0.05203% |
| 13 | 650 | 26169823 | 1.00625 | 26333384.1 | −0.05395% |
| 14 | 700 | 26140410 | 1.00734 | 26332280.6 | −0.05814% |
| 15 | 750 | 26109163 | 1.00853 | 26331874.1 | −0.05968% |
| 16 | 800 | 26075242 | 1.00981 | 26331040.1 | −0.06285% |
| 17 | 850 | 26038681 | 1.01119 | 26330053.6 | −0.06659% |
| 18 | 900 | 25999739 | 1.01267 | 26329156.1 | −0.07000% |
| 19 | 950 | 25959225 | 1.01423 | 26328624.5 | −0.07202% |
| 20 | 1000 | 25916479 | 1.01588 | 26328032.6 | −0.07426% |
| 21 | 1050 | 25870936 | 1.01761 | 26326523.6 | −0.07999% |
| 22 | 1100 | 25823584 | 1.01942 | 26325077.6 | −0.08548% |
| 23 | 1150 | 25774163 | 1.02131 | 26323410.5 | −0.09181% |
| 24 | 1200 | 25723526 | 1.02326 | 26321855.2 | −0.09771% |
| 25 | 1250 | 25671636 | 1.02528 | 26320614.7 | −0.10242% |
| 26 | 1300 | 25617889 | 1.02736 | 26318794.7 | −0.10932% |
| 27 | 1350 | 25563016 | 1.02951 | 26317380.4 | −0.11469% |
| 28 | 1400 | 25506991 | 1.03171 | 26315817.3 | −0.12062% |
| 29 | 1450 | 25449687 | 1.03397 | 26314212.8 | −0.12671% |
| 30 | 1500 | 25390639 | 1.0363 | 26312319.5 | −0.13390% |
| 31 | 1550 | 25330763 | 1.03869 | 26310810.7 | −0.13963% |
| 32 | 1600 | 25268285 | 1.04116 | 26308327.5 | −0.14905% |
| 33 | 1650 | 25204549 | 1.04371 | 26306240 | −0.15697% |
| 34 | 1700 | 25139013 | 1.04634 | 26303954.7 | −0.16565% |
| 35 | 1750 | 25071823 | 1.04907 | 26302097.1 | −0.17270% |
| 36 | 1800 | 25001965 | 1.05191 | 26299817 | −0.18135% |
| 37 | 1850 | 24930558 | 1.05485 | 26297999.4 | −0.18825% |
| 38 | 1900 | 24856230 | 1.0579 | 26295405.5 | −0.19810% |
| 39 | 1950 | 24779510 | 1.06108 | 26293042.4 | −0.20706% |
| 40 | 2000 | 24700898 | 1.06436 | 26290647.4 | −0.21615% |
| 41 | 2050 | 24619876 | 1.06775 | 26287872.1 | −0.22669% |
| 42 | 2100 | 24537541 | 1.07125 | 26285841 | −0.23440% |
| 43 | 2150 | 24452885 | 1.07483 | 26282694.2 | −0.24634% |
| 44 | 2200 | 24368062 | 1.07848 | 26280467 | −0.25479% |
| 45 | 2250 | 24282321 | 1.08218 | 26277841.9 | −0.26476% |
| 46 | 2300 | 24195538 | 1.08593 | 26274661 | −0.27683% |
| 47 | 2350 | 24109229 | 1.08971 | 26272068.2 | −0.28667% |
| 48 | 2400 | 24022755 | 1.09352 | 26269362.5 | −0.29694% |
| 49 | 2450 | 23936309 | 1.09737 | 26266987.8 | −0.30595% |
| 50 | 2500 | 23848192 | 1.10129 | 26263774.9 | −0.31815% |
| 51 | 2550 | 23759036 | 1.10532 | 26261338.2 | −0.32740% |
| 52 | 2600 | 23666544 | 1.1095 | 26258030.1 | −0.33995% |
| 53 | 2650 | 23570712 | 1.11387 | 26254709.2 | −0.35256% |
| 54 | 2700 | 23471248 | 1.11845 | 26251417.5 | −0.36505% |
| 55 | 2750 | 23369748 | 1.1232 | 26248900.8 | −0.37460% |
| 56 | 2800 | 23267349 | 1.12804 | 26246500.1 | −0.38371% |
| 57 | 2850 | 23166448 | 1.1328 | 26242952.3 | −0.39718% |
| 58 | 2900 | 23070843 | 1.13736 | 26239853.9 | −0.40894% |
| 59 | 2950 | 22976865 | 1.14191 | 26237512 | −0.41783% |
| 60 | 3000 | 22861848 | 1.14755 | 26235113.5 | −0.42693% |
| 61 | 3050 | 22657995 | 1.15774 | 26232066.6 | −0.43849% |
| 62 | 3100 | 22211497 | 1.18087 | 26228890.6 | −0.45055% |
| 63 | 3150 | 21242010 | 1.23464 | 26226235.5 | −0.46062% |
Conclusion
The following sections describe the advantages and disadvantages of both coherent and noncoherent sampling method prior to FFT.
Noncoherent Sampling
Advantages
Accurate harmonic contents can be obtained by following a proper FFT.
Noncoherent mode can perform sampling continuously using the ping pong buffer routine.
A continuous FFT process is possible.
Disadvantages
An FFT is difficult to perform and needs a more complex routine.
If signals are generated using a function generatorto perform the analysis, proper timing, and sync must be considered between the CLK_IN of the ADE9000 and the frequency of the generators.
Coherent Sampling
Advantages
An FFT is easier to perform, because 128 samples are constantly tracked during the resampling per line cycle.
Disadvantages
Coherent sampling is less accurate than the noncoherent sampling, because the maximum codes for resampled data is 18,196 codes.
Resampling is limited to 512 samples per waveform buffer.
Performing a continuous FFT is difficult, because portions of the signal are lost when the waveform buffer calculates resampled data.
The ADE9000 simplifies harmonic analysis by using the waveform buffer register. It is possible to calculate up to the 63rd harmonic and introduce the gain compensation factors to correct the attenuation caused by the digital filtering plus effects of the antialias filter.
