AN-1157: Tuning the Extended Kalman Filter in the ADIS16480
Introduction
The ADIS16480 is a MEMS inertial measurement unit (IMU) that includes a three-axis accelerometer, 3-axis gyroscope, 3-axis magnetometer, and a barometer. In addition to providing a fully calibrated, frame-aligned set of inertial MEMS sensors, the ADIS16480 also includes an extended Kalman filter (EKF) that computes dynamic orientation angles.
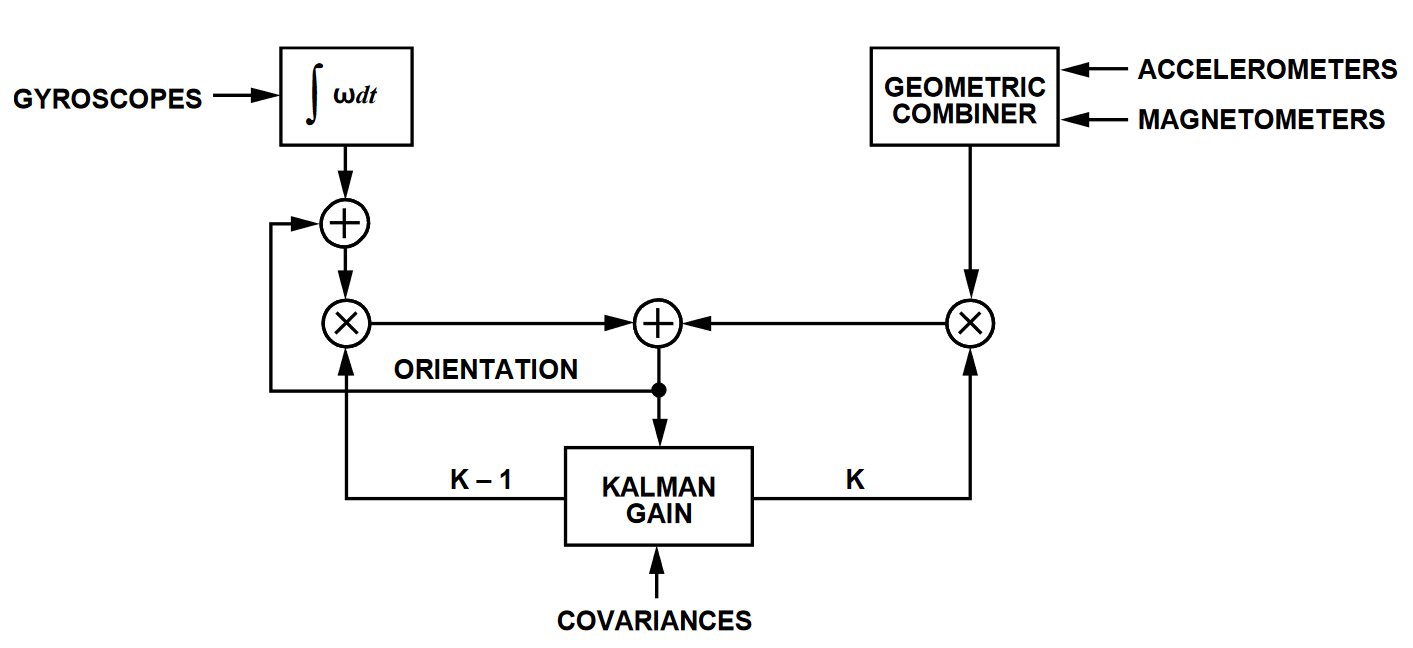
The EKF estimates the orientation angles using a combination of gyroscope, accelerometer, and magnetometer contributions. The accelerometers provide orientation angle measurements, with respect to the earth’s gravity. The magnetometers provide orientation angle measurements, based on the earth’s magnetic field. Figure 1 illustrates the EKF, using two separate data inputs: integrated gyroscope and present orientation, which is a geometric combination of accelerometer and magnetometer measurements. The Kalman Gain stage contains the weight factors, which determine the level of contribution from each of these paths in the final angle estimates. The ADIS16480 derives the weighting factors real-time, based on the covariance terms, which represent the level of uncertainty assigned to each sensor.
Optimal performance comes from selecting appropriate covariance values for the sensors, given the application environment. Selecting optimal covariance values can be an iterative process of test, observe, analyze, adjust, and test again. While this application note offers analytical tools for simplifying this process, there is no substitute for making application-specific observations and adjustments.
The ADIS16480 provides user write control for gyroscope bias, gyroscope rate random walk (RRW), and accelerometer and magnetometer covariance values in user-accessible registers (see Table 1). When using the adaptive EKF option in the ADIS16480, these registers update in real-time based on the conditions that the sensors are measuring.
| Register | Address1 | Key Frequency |
| QCVR_NOIS_UPR | 0x62 | Gyroscope noise, upper word |
| QCVR_NOIS_LWR | 0x60 | Gyroscope noise, lower word |
| QVCR_RRW_UPR | 0x66 | Gyroscope RRW, upper word |
| QVCR_RRW_LWR | 0x64 | Gyroscope RRW, lower word |
| RCVR_ACC_UPR | 0x6E | Accelerometer, upper word |
| RCVR_ACC_LWR | 0x6C | Accelerometer, lower word |
| RCVR_MAG_UPR | 0x72 | Magnetometer, upper word |
| RCVR_MAG_LWR | 0x70 | Magnetometer, lower word |
| 1All of these registers are located on Page 3 of the ADIS16480’s User Register Memory Map. Set PAGE_ID = 0x0003 (DIN = 0x8003) prior to accessing these addresses. | ||
Theoritical Covariance Values
Tuning the EKF is often an iterative process, since some of the error sources are difficult to model. One method for getting this process started is to assume that these error sources do not exist and set the covariance values equal to their theoretical noise and stability values. The starting value for the gyroscope noise covariance comes from the gyroscope’s total noise specification. Convert this number into units of radians/second and then square the value.
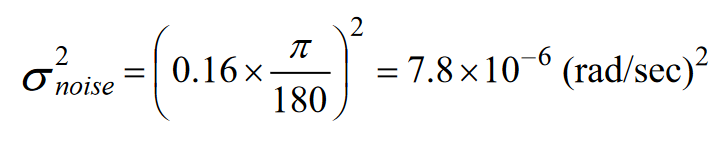
The starting value for the gyroscope’s RRW covariance can start with the in-run bias stability (6.25 °/hour).
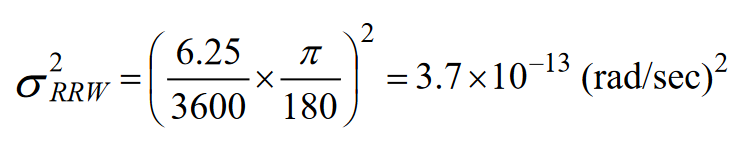
In practice, other contributions to long-term drift, including temperature drift, vibration and other linear acceleration, may require consideration for optimizing this parameter.
The covariance terms for the accelerometers and magnetometers come from their noise specification and use LSB2 as their units.
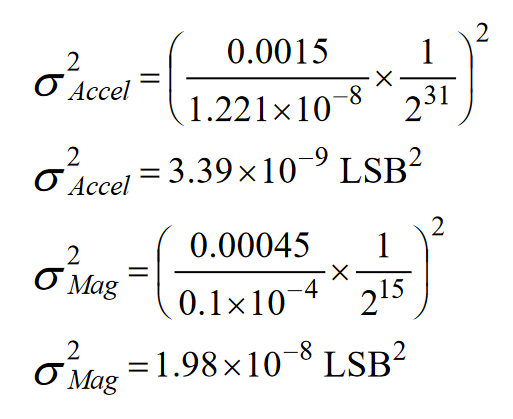
| Gyro Noise | 7.8 × 10-6 |
| Gyro Drift | 3.7 × 10-13 |
| Accelerometer | 3.39 × 10-9 |
| Magnetometer | 1.98 × 10-8 |
The default covariance values in the ADIS16480 are in Table 3 Note that the values are larger than the theoretical numbers, in order to account for typical, unmodeled error sources.
| Gyro Noise | 1 × 10-5 (rad/sec)2 |
| Gyro Drift | 5 × 10-11 (rad/sec)2 |
| Accelerometer | 4 × 10-9 LSB2> |
| Magnetometer | 3 × 10-8 LSB2 |
Adaptive Features
The ADIS16480 incorporates an algorithm using innovation residuals, which adaptively adjust the covariance terms of the accelerometers (RCVR_ACC_xxx) and magnetometers (RCVR_MAG_xxx). This algorithm adjusts the RCVR_ACC and RCVR_MAG registers in real time, allowing the user to observe the effects of varying environmental conditions. This feature can be very useful in the process of tuning the EKF.
The algorithm often generates covariance values, which are larger than the theoretical values computed. The difference is due to a number of unmodeled error sources, such as scale or offsets in the sensors, cross-coupling due to misalignments, and hard or soft iron magnetic distortions.
On-board temperature compensation minimizes temperaturedependent errors, but the residual errors are another contribution to larger covariance values.
Gyroscope scale factor errors are not modeled and contribute noise to the covariance terms. To provide some compensation, the ADIS16480 has a fading memory feature in EKF_CNFG[9]. Set EKF_CNFG[9] = 1 (DIN = 0x8003, 0xC102) to enable the fade memory function, which adds a percentage of the gyroscope rate to the variance, in order to account for the scale factor error. When the sensor is steady, there is no correction to the gyroscope covariance (Q) parameters, but increasing rotation rates result in increasing covariance to account for increased potential error. The adjustment to the Q values occurs internally to the part and is not observable by reading the QCVR_NOIS registers.
Tuning Guidelines
As described, the EKF algorithm estimates the ADIS16480’s orientation by optimally combining the measurements from the gyroscopes, accelerometers, and magnetometers. The covariance terms for each sensor determine the influence (weight) that they have on the angle estimates. Small covariance values indicate that a sensor has low noise relative to the other sensors and will provide reliable measurements. Therefore, their measurements have more weight in the final estimates.
Covariance terms provide an opportunity to suppress noisy influences associated with a particular application. Vibration is one condition that could warrant changes to the factorydefault, covariance terms. In this case, the values associated with RCVR_ACCL_xxx registers may increase, reducing the weight of the accelerometers, since accelerometer measurements will have vibration-related errors.
The presence of magnetic field disturbances and other error sources offer another example where covariance term updates can improve angle accuracy. In this case, increasing the values in the RCVR_MAG_xxx registers reduces the impact of the magnetic field errors. One trade-off associated with deweighting the accelerometers and magnetometers is in the ability to manage gyroscope saturation. Reduced accelerometer or magnetometer influences can result in a loss of angle tracking and cause a slow recovery from the saturation event. Another trade-off is that the device exhibits higher steady-state error. On the other hand, de-weighting the accelerometers and magnetometers tends to result in less noisy output.
If the errors in the magnetic fields are excessive with respect to the angle accuracy goals, EKF_CFG[1] provides a control bit for disabling the magnetometer influence over the angle measurements. Set EKF_CFG[1] = 1 (DIN = 0x8003, 0x5001) to disable the magnetometer influences on the angle estimates. Disabling the magnetometer influence forces the yaw angle to rely on the gyroscope only, resulting in an angle drift rate that is proportional to the gyroscope’s total bias error. Optimal performance involves getting the right balance among competing system requirements and is often not a trivial task.
Covariance adjustment is useful for compensating for consistent environmental noise, but for managing large, occasional disturbances, the ACC_DIST_THR and MAG_DISTB_THR registers provide user-programmable “disturbance levels”. The ADIS16480 continuously compares the three-dimensional against the stored values that reflect their state during the most recent EKF initialization process. When the magnitude differs by a percentage greater than or equal to the threshold specified in the ACC_DIST_THR or MAG_DISTB_THR registers, the affected measurement is temporarily disabled for the duration of the disturbance.
Magnetometer Soft and Hard Iron Influences
Hard and soft iron influences are a common error source associated with magnetometer measurements and tend to be application-specific. Before attempting to tune the EKF, characterize the magnetometer response while slowly rotating the ADIS16480 through a full 360° turn, around two of the three axes, while measuring all three magnetometers. Use these measurements to derive hard and soft iron correction factors, and then write these values to the SOFT_IRON_Sxx and HARD_IRON_x registers.
Trade Space
Tuning involves tradeoffs between dynamic and static performance. Tuning a filter for tracking high speed movement likely sacrifices steady-state accuracy. Conversely, tuning for static accuracy comes at the expense of bandwidth and the ability to track rapid movements. The application drives the relative importance of the two.
Tuning For Dynamic Performance
Tuning the EKF for dynamic conditions starts with developing a test approach that enables cause/effect analysis of covariance values. This test approach involves four basic parts: inertial motion profile, observable performance metrics, and analysis techniques and data collection. The following example illustrates these steps, which are useful in any application.
Inertial Motion Profile
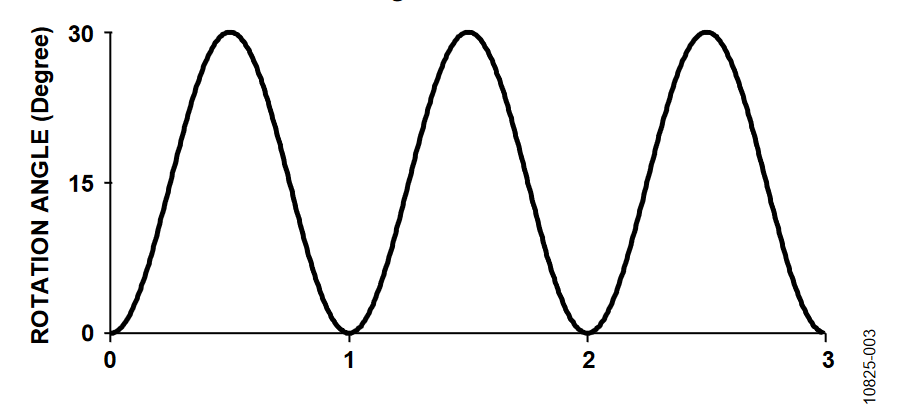
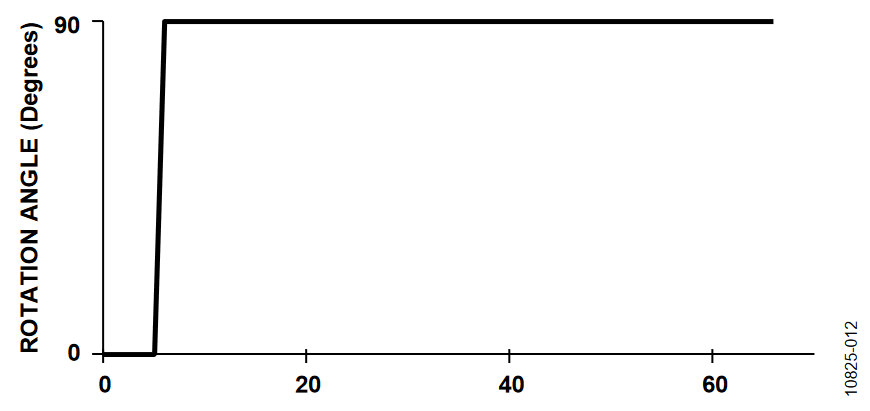
The inertial motion profile must include the ability to introduce inertial conditions that reflect the actual application conditions. Figure 2 shows the inertial conditions for this example involved, which utilizes a 1 Hz sinusoid rotation around the z-axis that rotates between 0 and 30 degrees.
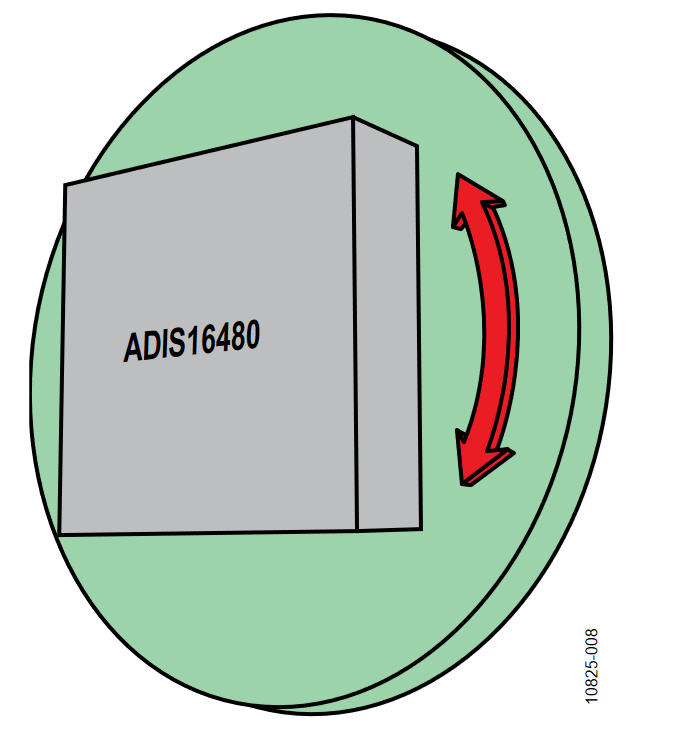
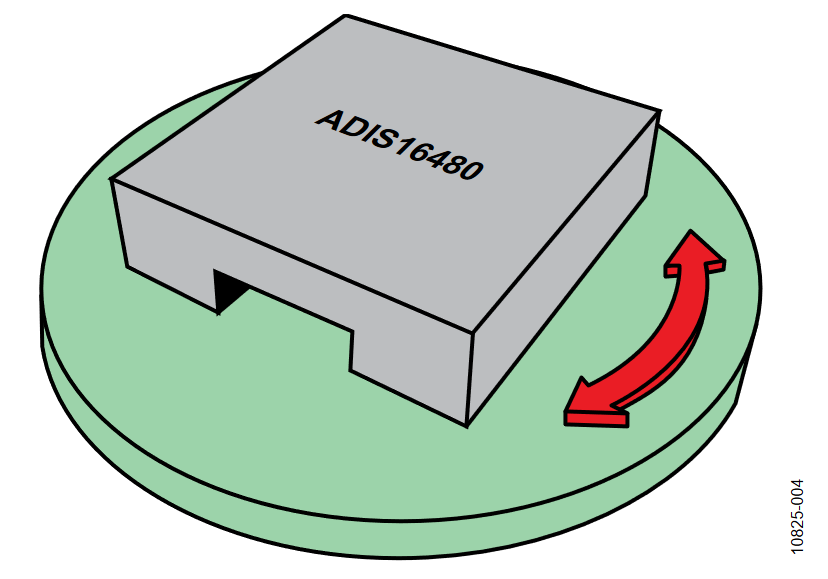
This profile also used two different orientations for the axis of rotation, with respect to horizon: horizontal (Figure 3) and vertical (Figure 4). When the axis of rotation is in a vertical orientation, the accelerometer outputs are largely unused since their output is constant. Setting the axis of rotation in a horizontal orientation and the plane of rotation aligned with magnetic north ensures that the gyroscopes, accelerometers, and magnetometers are all stimulated.
Observable Performance Metrics
The yaw angle output register, YAW_C32_OUT, provides the best output variable for observation, given the inertial motion profile of rotation about the z-axis.
Analysis Techniques
Using FFT analysis techniques, in order to measure signal to noise ratio (SNR), provides a simple accuracy metric, for the quality of inertial representation in the yaw-out register.
Data Collection
The ADIS16480 output date rate of 2460 (DEC_RATE = 0x0000) and a data record length of 35200 samples is sufficient for representing the inertial motion.
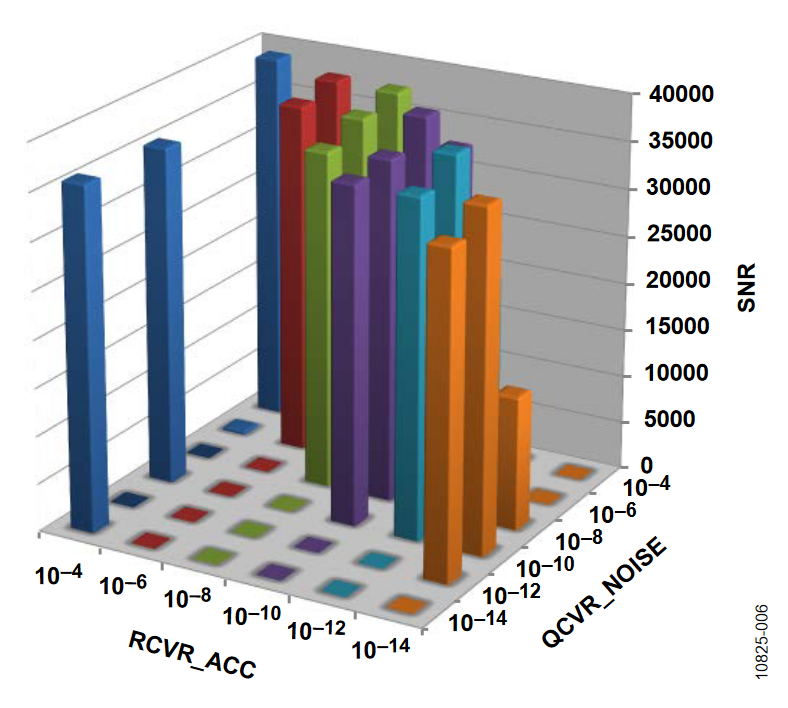
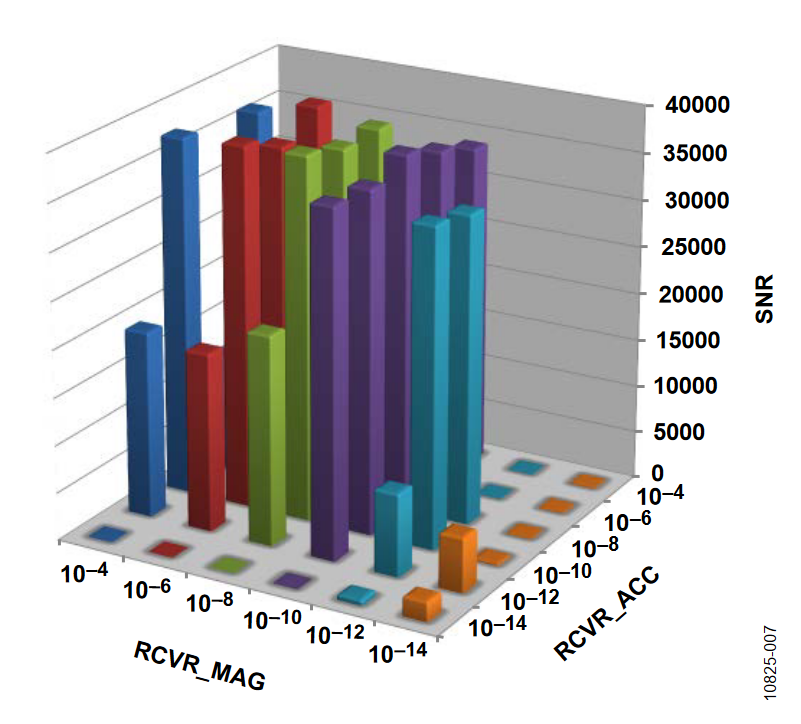
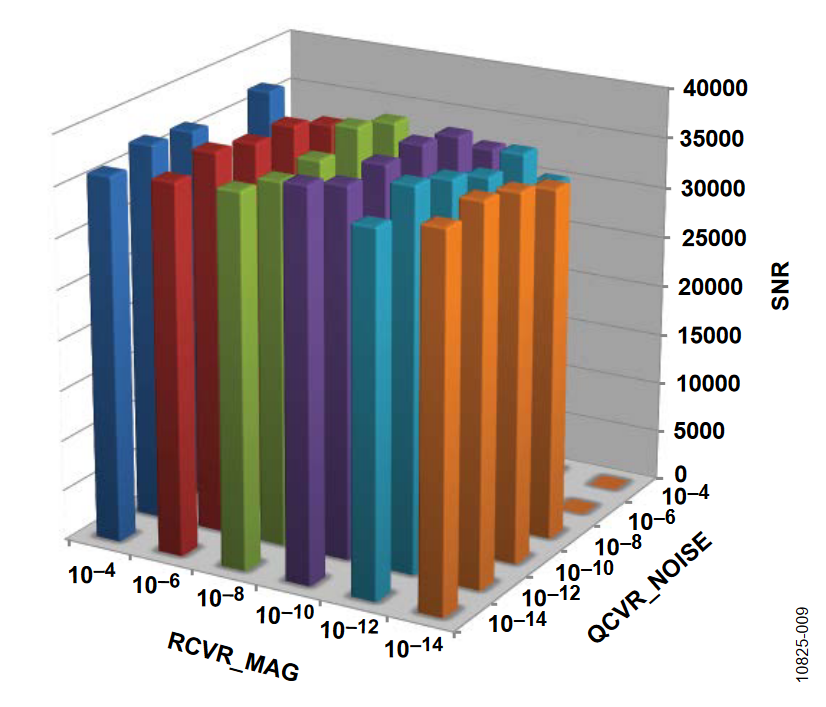
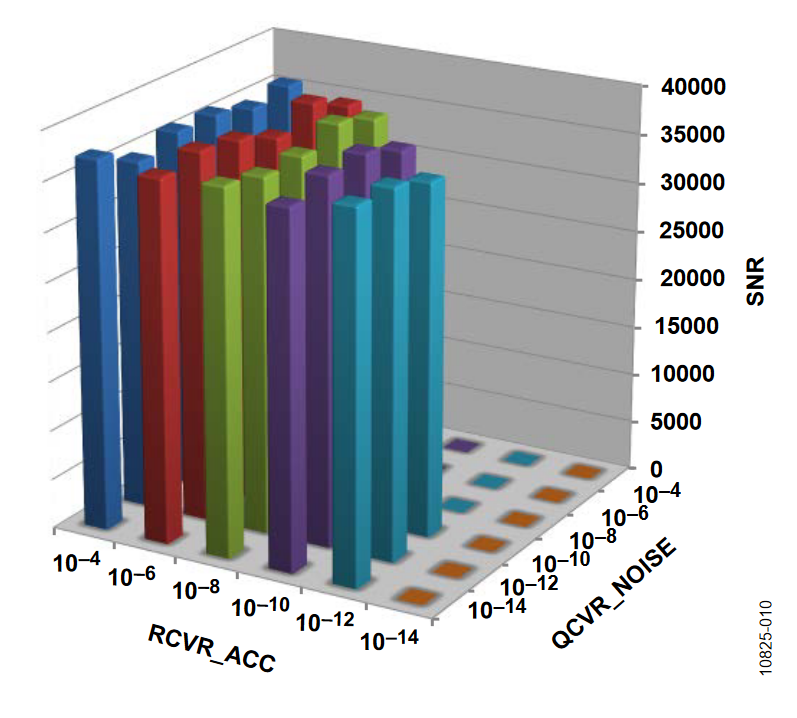
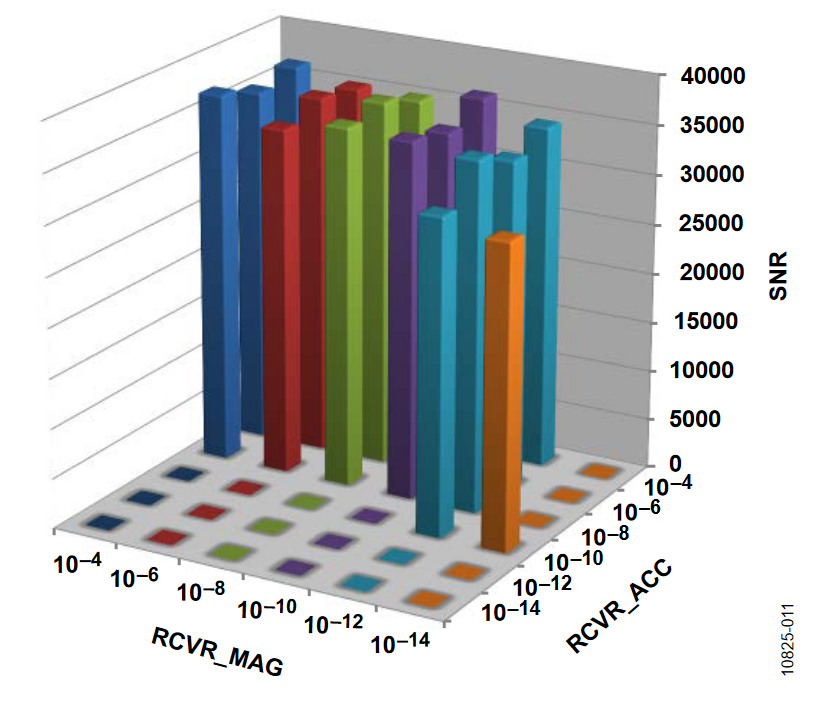
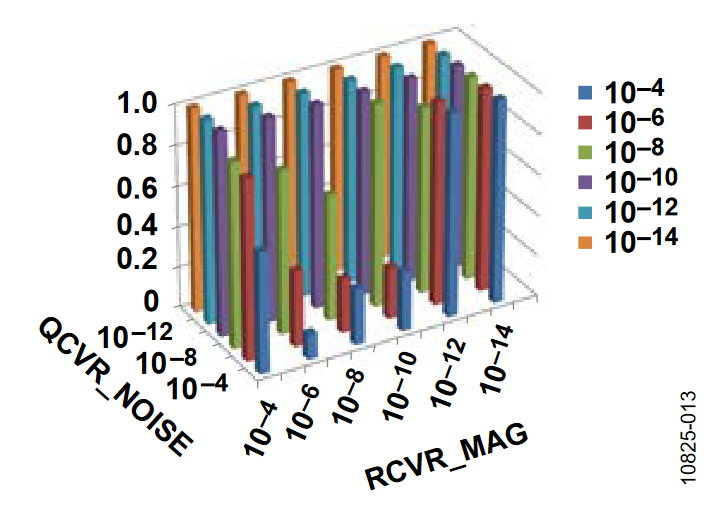
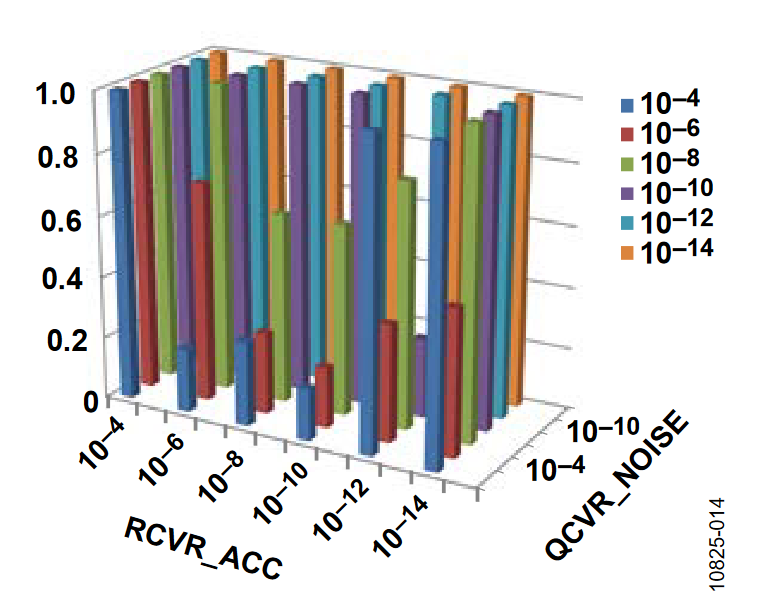
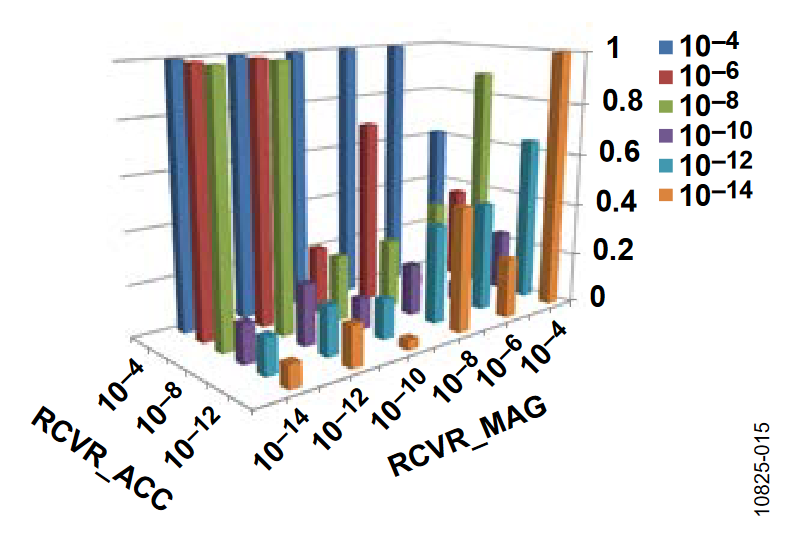
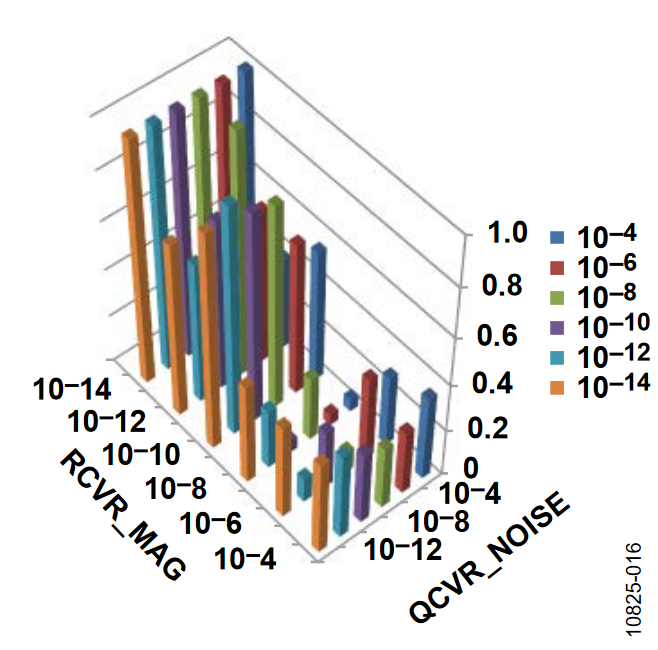
The 3D bar charts plot the SNR observed for a number of covariance settings. In all cases, the gyro drift covariance, QCVR_RRW, is set to 10-12. Of the three remaining covariance terms, one value is fixed on a particular figure (indicated in the figure title) and the bar levels indicate the SNR observations, which are associated with several discrete settings (between 10-14 and 10-4) It is evident that the two rotation orientations produced different results. With the axis of rotation in the horizontal orientation, the ADIS16480 operates with a larger range of covariance terms.
Vertical Orientation
The following plots of the signal-to-noise ratio (SNR) were measured with the axis of rotation in the vertical orientation.
Horizontal Orientation
The following plots of the SNR were measured with the axis of rotation in the horizontal orientation.
Tuning For Static Accuracy
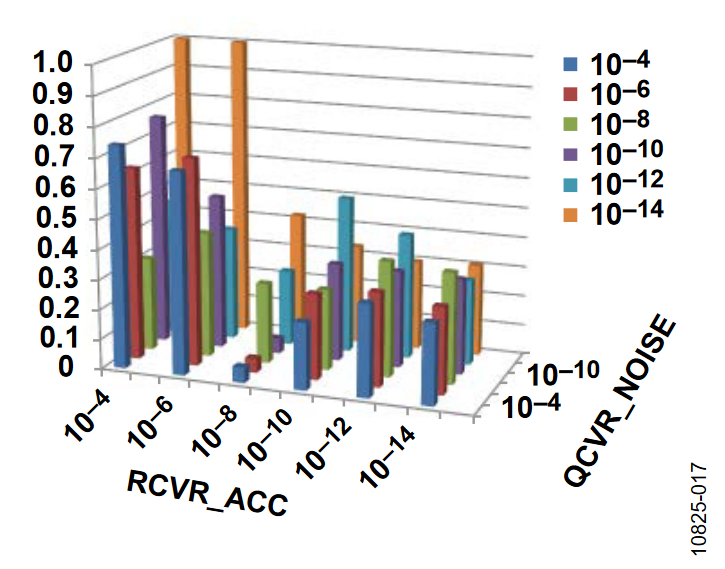
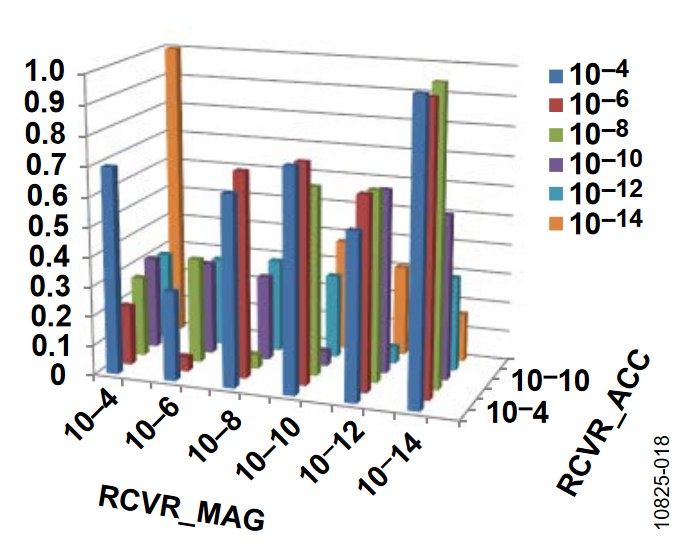
In the test designed to check static accuracy, the starting orientation is noted, the sensor is rotated 90°, and then the ending orientation is subtracted from the starting value.
As in the dynamic tests, the covariance for the gyro drift is fixed at 1e-12, one of the other covariances is fixed at a nominal value, and the other two are varied from 1e-14 to 1e-4.
Vertical Orientation
Figure 12 to Figure 14 provide the response for the different covariance terms, with the axis of rotation in the vertical orientation. The differences between the ideal 90° and the measured orientation are plotted. The error is capped at 1° so that smaller errors are not visually overwhelmed.
Horizontal Orientation
Figure 15 to Figure 17 were obtained with the axis of rotation in the horizontal orientation.
Conclusion
Tuning a Kalman filter for optimal performance is largely a trial-and-error effort. This application note outlines a methodical approach that can help find an adequate combination of covariance values. Since each SNR reading uses a large step size, fine tuning may be essential for refinement in the final application.
While the results presented here will not apply to all applications, they can serve as a starting point for selecting initial covariance values to test. Depending on required specifications, it may be prudent to check both static and dynamic performance and then select the optimal mix.