AN-1002: The AD9548 as a GPS Disciplined Stratum 2 Clock
Introduction
The synchronous optical network (SONET) is the backbone of most of the world’s day-to-day communication systems. Its stringent requirements with regard to the clocking signals that synchronize the system allow for reliable transmission of data across a multitude of interlinked systems spread out around the globe. The system is comprised of a hierarchy of precision timing units categorized according to their accuracy and drift performance criteria, that is, the stratum levels. Stratum 1 is the most demanding level with timing accuracies only possible with atomic clocks. The timing performance requirements become more relaxed with increasing stratum level numbers (Stratum 2, Stratum 3E, Stratum 3, Stratum 4). Focusing on Stratum 2, there are two primary requirements (see the clock requirements summary table in the GR-1244-CORE SONET standard, “Clocks for the Synchronized Network: Common Generic Criteria” available from Telcordia Technologies):
- 1.6 × 10−8 or 16 part per billion (ppb) free-run accuracy over a period of 20 years with no outside reference
- 1 × 10−10 or 0.1 ppb stability over a period of 24 hours in holdover mode
The holdover stability requirement implies a certain cumulative time error (CTE), for which an estimate is possible according to the following equation from C. W.T. Nicholls’ and G.C. Carleton’s paper, “Adaptive OCXO Drift Correction Algorithm” (see the References section):
Δf/f0 = Δt/T
where:
Δf/f0 is the static frequency stability.
T is the holdover period.
Δt is the CTE estimate.
Based on the Stratum 2 specification, for which Δf/f0 = 10−10 and T = 86,400 seconds (24 hours), the calculation yields a CTE of 8.64 μs/day.
The holdover requirement adds significant cost to a Stratum 2 timing unit because the full burden of the stability requirement falls on the clock’s local timing source. Assuming the local clock source is an oven-controlled crystal oscillator (OCXO), then only the most stable (that is, expensive) ones are viable options. Consequently, as the number of Stratum 2 compliant installations increases so does the pressure to find a low cost solution.
This application note proposes the feasibility of a relatively low cost solution using the Analog Devices, Inc. AD9548 digital phase-lock loop (PLL). The solution is based on Nicholls and Carleton’s paper and demonstrates the ability to provide holdover stability of 0.017 ppb (a CTE of 1.5 μs/day) using an OCXO with a stability of 0.45 ppb (a CTE of 38.9 μs/day). Note that the 0.45 ppb OCXO stability comes from 0.4 ppb for temperature and 0.05 ppb for aging. The Nicholls and Carleton paper describes an adaptive drift correction algorithm (hereafter referred to as the N/C system) that compensates for the OCXO’s drift characteristics during holdover.
Before proceeding, read Appendix A for a synopsis of the N/C system. Becoming familiar with the N/C system is helpful because this system is compared with the proposed AD9548- based system (hereafter referred to as the proposed system) occurs throughout the remainder of this document.
An Overview of the AD9548
Comparing these two solutions requires an introduction to the basic functionality of the AD9548 (see Figure 1). The AD9548 requires a clock source (the SYSCLK terminal) to drive its internal timing functions and to clock its embedded direct digital synthesizer (DDS) and digital-to-analog converter (DAC). The DDS/DAC operates with a clock rate between 500 MHz and 1 GHz. To simplify accommodation of the high internal clock rate, the AD9548 provides a system clock generator that contains an optional analog PLL synthesizer. The user may drive the SYSCLK input directly with a frequency source of 500 MHz to 1 GHz, or use a low frequency source and have the system clock generator PLL synthesize a 900 MHz to 1 GHz internal clock.
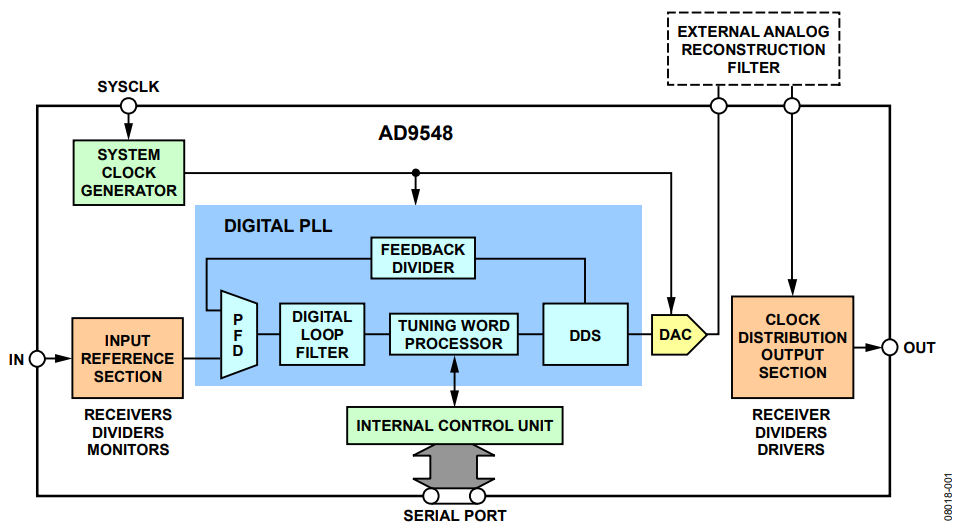
Figure 1. AD9548 Simplified Block Diagram.
The heart of the AD9548 is its digital PLL. Consider an analog PLL, in which a phase-frequency detector (PFD) drives an analog charge pump and loop filter to produce a voltage that controls the output frequency of a voltage-controlled oscillator (VCO). The AD9548’s digital PLL, on the other hand, has a PFD with a numeric output that drives a digital loop filter that delivers numeric frequency tuning words to a DDS. The DDS, in turn, drives a DAC that produces a sinusoidal analog signal at a frequency determined by the frequency tuning word at the DDS input. Note that the DDS also drives the feedback path of the digital PLL.
The key point to note is that the output frequency of the digital PLL depends on the value of a numeric frequency tuning word, not an analog voltage (as is the case with a VCO-based analog PLL). In the AD9548, the value of a 48-bit frequency tuning word (M) at the DDS input generates a DDS output frequency (fDDS) given by
fDDS = (M/248) × fS
where fS is the frequency supplied by the system clock generator. The resulting tuning precision is 3.55 × 10−6 ppb (relative to fS). Furthermore, the PFD can measure the time offset between the feedback and reference clock edges to within 0.5 ps. The digital loop filter also relies on numeric coefficients to establish the loop bandwidth of the digital PLL. These coefficients are programmable, so the user can adjust the loop bandwidth over a range from 0.001 Hz to 100 kHz.
The output of the digital PLL (the DAC) drives a clock distribution section that ultimately produces the desired output signal at the OUT terminal. Although the OUT terminal in Figure 1 appears to be a single output, it actually represents four pairs of independently selectable output signals. Each pair of output signals has a dedicated optional frequency divider. However, the topic of this application note requires the use of only one output signal allowing the user to ignore the extra outputs.
The serial port allows the user to control the functionality of the AD9548 via an external processor. The serial port is of particular importance to the system proposed in this application note and gives the user access to the DDS input. That is, the user can read the currently active DDS frequency tuning word or write a specific DDS frequency tuning word (thereby forcing a desired output frequency). This functionality is critical to implementing the drift correction algorithm described in Nicholls’ and Carleton’s paper (see the References section).
In closed-loop operation, the digital PLL locks to the reference clock signal applied at the IN terminal. It does so by steering the DDS output frequency (digitally) until the frequency of the feedback signal matches the frequency of the reference signal and the edges of both signals become time aligned. Although the IN terminal in Figure 1 appears to be a single input, it actually represents up to eight independent selectable input signals. However, the proposed AD9548-based system described in this application note requires the use of only one input signal allowing the user to ignore the extra inputs.
The AD9548 also provides holdover functionality. When the input reference is lost, the device can automatically switch to holdover operation. In holdover mode, the digital PLL no longer controls the DDS output frequency. Instead, DDS control originates from the serial port or from an internal processing unit that maintains a piece-wise moving average of previously applied frequency tuning words. This functionality, too, is useful for implementation of the drift correction algorithm described in Nicholls’ and Carleton’s paper.
Proposed Stratum 2 Clock Solution
System Similarity and Contrast
The proposed solution is shown in Figure 2, which shares some common elements with Figure 3 in Appendix A (the N/C system). These elements include the OCXO, temperature sensor, GPS receiver, drift correction algorithm, and processor (the implementation of the adaptive oscillator model in Figure 3 implies a processor). Less obvious are the digital phase detector and frequency divider in Figure 3, which appear in the AD9548 digital PLL in Figure 2 as the PFD and feedback divider, respectively.
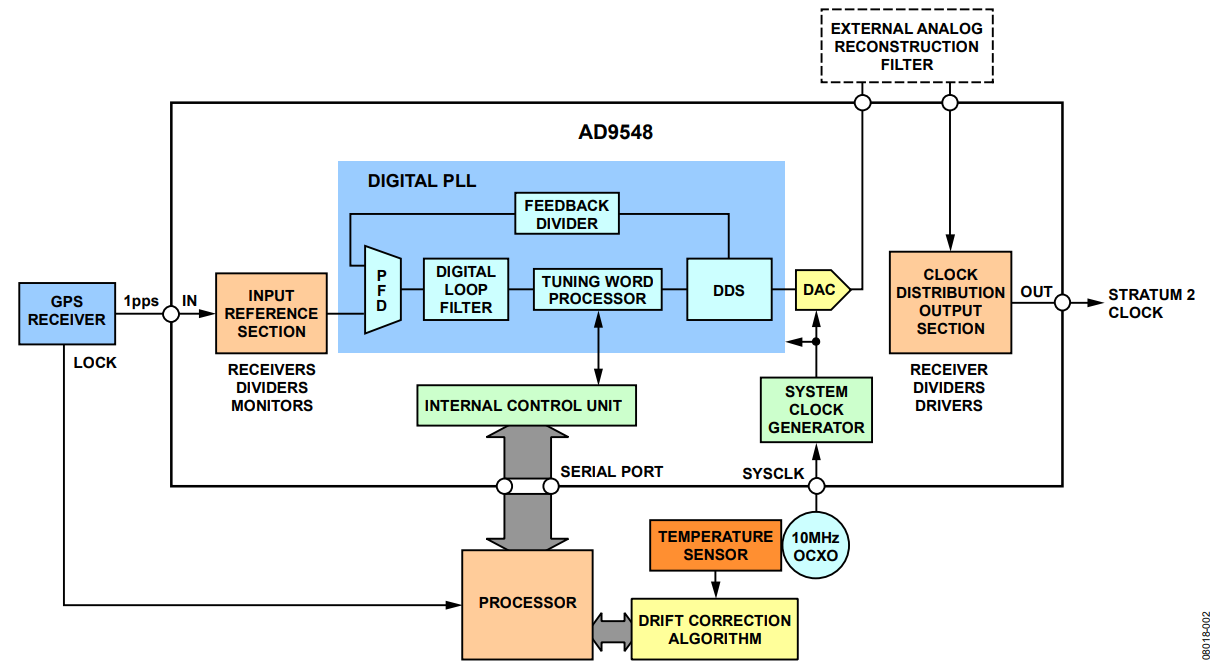
Figure 2. Proposed GPS Disciplined Stratum 2 Clock.
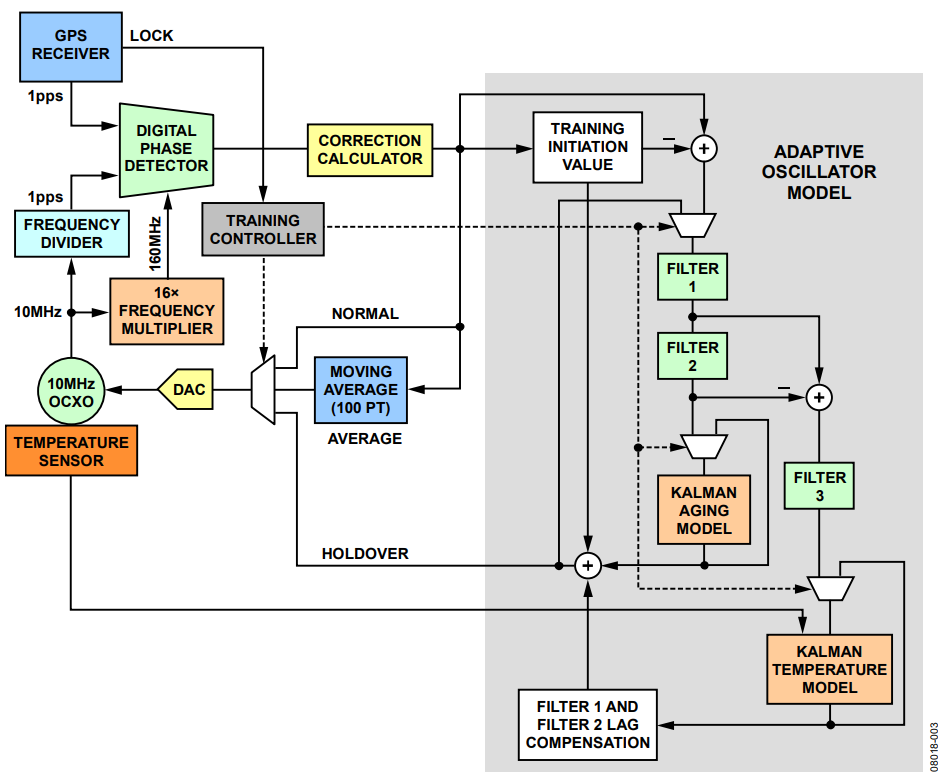
Figure 3. Functional Diagram of the Adaptive Control Mechanism in Nicholls' and Carleton's Paper.
There are also some differences between the proposed solution and Figure 3. One is that the processor in Figure 2 takes on the role of the training controller, correction calculator, and the 100 pt moving average (MA) function in Figure 3. Another is that the AD9548 system clock generator in Figure 2 provides a function similar to the 16× frequency multiplier in Figure 3, but produces 1 GHz instead of 160 MHz.
The proposed solution must meet both the free-run and holdover requirement of a Stratum 2 clock. The GPS receiver satisfies the free-run requirement by virtue of the atomic clocks that reside within each GPS satellite. Therefore, the 1 pps output of the GPS receiver exhibits the requisite long-term frequency precision. The fact that the AD9548 is phase-locked to the 1 pps output signal of the GPS receiver means that the long-term frequency accuracy of the GPS signal transfers to the AD9548 output (that is, the Stratum 2 clock signal).
Satisfaction of the holdover requirement, however, relies on the OCXO, AD9548, processor, temperature sensor, and drift correction algorithm. Assuming that the inherent stability of the OCXO does not satisfy the holdover requirement, the proposed solution circumvents this problem by using the processor to monitor the OCXO frequency periodically (by sampling the tuning word of the AD9548 DDS) so long as the GPS signal is present. Monitoring the OCXO frequency over time allows the adaptive oscillator model (drift correction algorithm) to learn the drift behavior of the OCXO over time and temperature. When the GPS signal disappears, thereby invoking holdover operation, the learned behavior allows the adaptive oscillator model to predict the drift behavior of the OCXO over time and temperature and to compensate accordingly.
Frequency Control Parameter
The learning and prediction mechanism relies on the availability of a system parameter linearly related to the output frequency. The system parameter is the variable that is learned and predicted in order to control the output variable (frequency, in this case). In the N/C system, the system parameter is the digital control word applied to the DAC, which controls the output frequency directly via the frequency control port of the OCXO. In the proposed system, the system parameter is the digital frequency tuning word applied to the DDS, which controls the output frequency of the DDS rather than the OCXO frequency directly (the OCXO is free to drift). Therefore, a slight difference exists in the way the system parameter operates with respect to both systems. However, if each of the system parameters linearly relates to the final output frequency, then both systems are functionally equivalent (their only difference being a constant scale factor). In fact, the necessary linear relationship exists (see Appendix B for details).
Proposed System Function and Comparison to the N/C System
In the N/C system, the correction calculator maintains a 2000 pt moving average (MA) of the system parameter. In addition, it accumulates the second-by-second time error provided by the digital phase detector with a timing resolution of 6.25 ns (compared with the 0.5 ps timing resolution of the AD9548 digital phase detector). In the N/C system, the accumulated output of the phase detector serves as the CTE. However, the GPS receiver signal introduces large instantaneous perturbations on the CTE because of its inherent jitter (a 1σ jitter magnitude of 50 ns/sec (50 ppb/sec)). To mask the GPS receiver jitter noise, the correction controller divides the CTE by 150 (a damping factor), thereby reducing the 1σ jitter magnitude to 0.33 ns/sec (0.33 ppb/sec). The correction calculator determines the correction value (System Parameter X) as follows:
X = MA – CTE/150
In the proposed system, the correction value (System Parameter Y) is not a linear calculation, but is the automatic result of the control loop. The 1 pps GPS receiver signal is the reference input to the digital PLL within the AD9548. With the AD9548 digital loop filter set to a bandwidth of 1/150 Hz (0.0067 Hz), the 1σ jitter magnitude of the GPS receiver effectively reduces to the same 0.33 ppb/sec jitter as stated for the N/C system. The reason is that the 1σ jitter magnitude is proportional to the jitter bandwidth. A reduction in bandwidth by a factor of 150 (1 Hz vs. 1/150 Hz) yields a proportional reduction in jitter (50 ppb/sec vs. 0.33 ppb/sec). The output of the digital loop filter serves as the correction value (Y) in the proposed system. Furthermore, there is no need to maintain a 2000 pt MA like the N/C system, because the loop filter essentially performs a time averaging function on the samples from the PFD and effectively smoothes out the jitter transients inherent in the 1 pps signal from the GPS receiver.
Recall that the N/C system uses a damping factor of 150 to attenuate the jitter transients associated with the 1 pps signal from the GPS receiver. This is the case for normal operation. However, to reduce the loop capture time during initial acquisition of the 1 pps GPS reference signal or during recovery from holdover, the N/C system reduces the damping factor to unity. The proposed system is capable of the same functionality by using the profile feature of the AD9548. A profile constitutes a set of parameters within the AD9548, which provides up to eight independent profiles. Each profile includes the digital loop filter coefficients as part of its parameter set. By programming one profile with a 0.0067 Hz bandwidth and another with a 10× wider bandwidth (for example, 0.07 Hz), the external processor can command the AD9548 to switch between the two profiles as required.
The N/C system uses the training controller to handle the timing and signal routing for training the adaptive oscillator model (AOM) and for determining when to switch to holdover operation. The proposed system handles this same functionality via the external processor. In both systems, the AOM requires a 2-hour training period to learn the characteristics of the OCXO behavior over time and temperature. Furthermore, the training process must occur in the presence of the GPS signal in order for the model to learn the drift characteristics of the OCXO relative to an accurate frequency standard (the GPS receiver). This implies that the control loop that locks the OCXO output signal to the GPS receiver completely stabilizes before training begins, otherwise the AOM learns the behavior of the loop response rather than the OCXO drift. Unfortunately, the low bandwidth of the control loop means that it takes nine hours for the loop to stabilize to a level suitable for the AOM. Together the loop stabilization and training periods span a total of 11 hours. Fortunately, this meets the Stratum 2 requirement, which allows up to 12 hours for establishing an estimate of the input reference frequency for holdover operation.
During the 2-hour training period of the AOM, the training controller in the N/C system routes the correction signal (that is, System Parameter X) to the AOM input. In the proposed system, the processor has the ability to read the frequency tuning word present at the DDS input of the AD9548 (that is, System Parameter Y). Therefore, in the proposed system the external processor periodically samples the DDS tuning words and delivers them to the AOM as required.
The N/C system provides two alternatives for holdover operation depending on the training status of the AOM. If the 1 pps GPS signal is present long enough to allow training of the AOM, then the frequency control signal (System Parameter X) is the output of the AOM during holdover. Otherwise, the holdover frequency control signal is a static value represented by the most recent 100 pt MA of X.
The proposed system handles the two holdover alternatives as follows. Initialization occurs the moment the GPS receiver first indicates lock. The external processor starts monitoring elapsed time and the AD9548 digital PLL automatically starts to acquire the 1 pps GPS signal. By programming the AD9548 holdover accumulation timer so that it provides updates at intervals of 1 sec, the processor can read the currently active frequency tuning word from the AD9548 (System Parameter Y) on a second-by-second basis. The processor maintains a running 100 pt MA of the Y values and writes each new MA value to the AD9548’s free-run frequency tuning word register.
Assuming that the GPS receiver remains locked for 9 hours, the external processor not only continues to deliver Y values to the 100 pt MA and deliver the MA to the AD9548’s free-run frequency tuning word register, but also starts routing the Y values to the AOM input. This marks the beginning of the 2-hour AOM training period, during which the AOM learns the OCXO drift behavior.
If the GPS receiver loses lock anytime before the full 11-hour training period expires, the processor immediately programs the AD9548 to user free-run mode, which forces the AD9548 output to the static frequency programmed into its free-run frequency tuning word register (the 100 pt MA with no OCXO drift correction). When the GPS receiver returns to a lock condition, then the whole process resumes at initialization.
On the other hand, if the GPS receiver remains locked for the full 11-hour training period, the processor no longer maintains the 100 pt MA, but continues to deliver Y values to the AOM at one-second intervals. This ensures that the training of the AOM remains up to date. The processor also delivers each newly retrieved Y value to the AD9548 free-run frequency tuning word register (instead of applying it to the 100 pt MA).
Once the AOM training period has been satisfied, if the GPS should lose lock, then the processor immediately programs the AD9548 to user free-run mode. This forces the output frequency of the AD9548 to the most recent Y sample value (previously stored in the free-run frequency tuning word register). Now, instead of reading a Y value from the AD9548 with each elapsed second, the processor increments the AOM, extracts the AOM output value and delivers it to the AD9548 free-run frequency tuning word register. Because the AD9548 is in user free-run mode, the free-run frequency tuning word immediately becomes the active DDS tuning word causing the AD9548 output frequency to track the AOM output. Therefore, because the AOM output represents a drift-corrected Y value, the AD9548 output maintains frequency stability similar to that experienced while the 1 pps GPS signal was available. Then, should the GPS receiver return to a lock condition (identifying the end of holdover operation), the whole process resumes at initialization.
Conclusion
Nicholls’ and Carleton’s paper (see the References section) addresses a solution for CDMA base stations. The N/C system demonstrates the ability to yield a cumulative time error of 1.5 μs/day during holdover operation. Although targeted for CDMA base station applications, the level of performance achieved by the N/C system also satisfies the 8.64 μs/day holdover requirement for a Stratum 2 clock.
This application note shows that an AD9548 combined with the principles described by Nicholls and Carleton yields performance comparable to the N/C system. As such, it offers compelling evidence for the feasibility of a Stratum 2 holdover compliant clock using an OCXO with Sub-Stratum 2 holdover stability performance. The ability to use an OCXO with relaxed stability performance implies a cost reduction relative to a solution that relies on a frequency standard that intrinsically meets the Stratum 2 requirement.
Furthermore, the AD9548 solution allows the user to specify an OCXO with a relaxed absolute frequency requirement. The reason is that the AD9548 corrects for any absolute frequency offset inherent in the OCXO via its 48-bit frequency tuning resolution. However, the intrinsic stability of the OCXO is still a necessary requirement, because the stability criteria relate to the holdover requirements. By relaxing the absolute frequency requirement, the user should be able to negotiate a lower unit cost from the OCXO manufacturer. The reason is that the OCXO manufacturer can realize increased yields by easing the absolute frequency requirement normally imposed on the OCXO production process.
Furthermore, the AD9548 solution provides the added benefit of a programmable, rather than fixed, final output frequency. The reason is that the output frequency depends on the programmed value of the feedback divider of the digital PLL of the AD9548. Specifically, with a 1 Hz reference frequency (as provided by the GPS receiver) the DDS output frequency is 1 Hz times the value of the feedback divider (NFDBK). For example, if NFDBK = 155,520,000, then fDDS = 155.52 MHz (the SONET OC3 rate).
Appendix A
Overview
Nicholls’ and Carleton’s paper provides a detailed explanation of the adaptive drift correction algorithm. Figure 3 captures its salient features, which gives the user a link between the proposed AD9548-based solution and the work done by Nicholls and Carleton.
The OCXO (10 MHz, nominal) drives both a frequency divider and a 16× frequency multiplier. The divider generates a 1 pulse per second (pps) signal and the multiplier a 160 MHz signal.
The output of a DAC provides fine-tuning of the OCXO output frequency. The DAC receives its input from the correction calculator, a 100 pt moving average of the most recent correction values, or the output of the adaptive oscillator model (AOM) as directed by the training controller.
The GPS produces a 1 pps output signal that exhibits 1σ edge timing jitter of 50 ns (50 ppb/sec), which is typical of GPS receivers and serves as the reference input to the system. The 1 pps GPS signal and the 1 pps OCXO-generated signal appear at the input of a digital phase detector with 6.25 ns timing resolution (derived from the 160 MHz signal synthesized from the OCXO output).
Correction Calculator
The correction calculator (see Figure 4) uses the output of the digital phase detector to compute the DAC codes for controlling the OCXO output frequency. First, the correction calculator multiplies the phase detector output by the sampling period, T, which is 1/(160 MHz) to arrive at the timing difference between the two 1 pps input signals. The correction calculator accumulates the timing errors from the phase detector, which yields the cumulative time error (CTE). It divides the CTE by 150 to soften the impact of the 50 ns/sec jitter (1σ) from the 1 pps GPS receiver output. This reduces the 1σ jitter component to 0.33 ns/sec. The correction calculator also maintains a 2000 pt moving average of the timing errors (MEAN_VAL), which is essentially a low-pass filter with a bandwidth of 220 μHz. The correction calculator then subtracts the softened CTE from MEAN_VAL to produce the correction signal (X). That is, X = MEAN_VAL − CTE/150, which constitutes the normal input to the DAC.
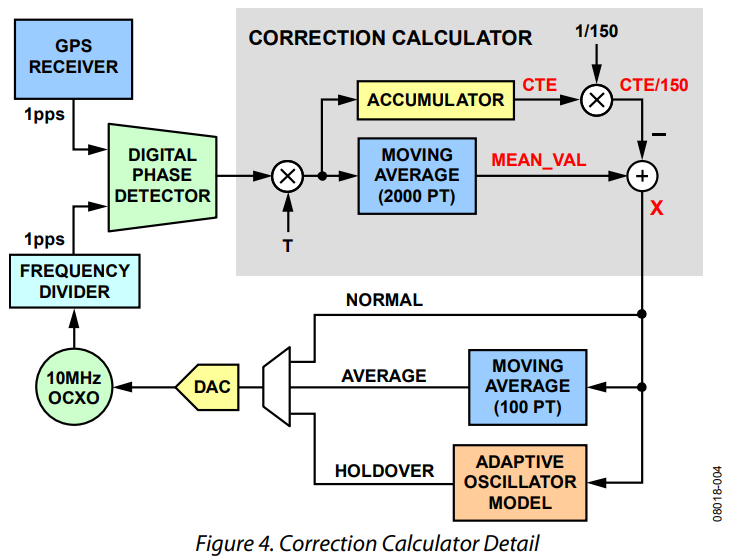
Figure 4. Correction Calculator Detail.
Training Controller
The training controller monitors the GPS satellite lock status and selects between the normal and holdover correction signals, accordingly. However, if the GPS receiver experiences a loss of lock before the AOM has time to settle, the controller selects the average signal instead of the holdover signal. The controller also controls the multiplexers in the AOM during its initial training period.
Closed-Loop Operation
The normal correction signal results from the closed feedback loop that includes the phase detector, OCXO, and the correction calculator, which together constitute a digital PLL. The 1 pps reference signal from the GPS governs the long-term stability of the OCXO output while the feedback loop tracks out any drift associated with the OCXO.
Open-Loop Operation
When the system switches to holdover operation, the GPS reference signal and the feedback loop are no longer in effect. Therefore, the OCXO becomes the sole frequency source and any drift exhibited by the OCXO appears in the output signal. Because the OCXO does not intrinsically satisfy the system stability requirement, the system relies on the AOM to improve on the OCXO’s stability performance during holdover operation.
Digital Filters Within the AOM
The AOM relies on two Kalman filters to model and predict temperature and aging correction factors for the OCXO using a linear model for each: for a description of Kalman filters, the requisite equations, and a practical implementation example (including MATLAB code) see the References section. The temperature model requires a temperature sensor as an input to correlate the frequency drift of the OCXO with temperature when the system is operating normally and to predict temperature-related drift when the system switches to holdover operation. In addition to the Kalman filters, the AOM contains three digital IIR filters:
- Filter 1: Basic 1-pole response with a bandwidth of 80 μHz.
- Filter 2: Elliptical 3-pole response with a bandwidth of 3 μHz, stop-band attenuation of 80 dB, and pass-band ripple of 1.5 dB peak-to-peak.
- Filter 3: Basic 1-pole response with a bandwidth of 80 μHz.
Filter 1 attenuates the high frequency components of the GPS receiver noise but passes the highest rate of change of stability vs. temperature (1.48 × 10−5 ppb/sec) and aging (5.8 × 10−7 ppb/sec) of the OCXO. Filter 2 attenuates the temperature component of the correction signal but passes the aging component to the Kalman aging model. Subtracting the aging component from the output of Filter 1 leaves the temperature component, which passes to Filter 3. Filter 3 further attenuates the GPS receiver noise and suppresses the transients introduced by the subtraction process, but passes the temperature component to the Kalman temperature model.
Training the AOM
As with any adaptive system, it is necessary to train the AOM. The training controller manages this training process, which takes a total of 11 hours. The first nine hours constitute nothing more than a delay to allow the digital PLL to stabilize after closing of the loop and to allow the OCXO to stabilize following a cold start. The remaining 2 hours is the actual training time that the AOM requires for its Kalman filters to reach sufficient convergence.
Subtraction of the value of the OCXO correction value at the start of the 2-hour training period (training initiation value) from the correction signal applied to the input of the AOM occurs to remove the initial transient from the training process. The result is much quicker convergence of the adaptive algorithms. However, note the adding of the training initiation value at the AOM output to compensate for its subtraction at the beginning of the process. Furthermore, Filter 1 and Filter 2 introduce a delay relative to the AOM input signal that also appears in the predictions made by the temperature and aging models. Thus, a lag compensation computation is also added to the AOM output to properly time align the AOM predictions with the input signal.
System Calibration
In addition to training the AOM, the training controller performs a calibration procedure on the normal feedback path of the digital PLL to determine the gain (K) of the control mechanism. K is the product of the DAC gain (KDAC) and the OCXO gain (KVCO). KDAC is nominally 5/220 V/bit and KVCO is nominally 200 ppb/V, so K is nominally 0.001 ppb/bit. However, KDAC varies from DAC to DAC and KVCO varies from OCXO to OCXO, which means that K is device dependent. The calibration procedure involves taking an exact measurement of K, which removes the device dependency and enhances the robustness of the system.
Appendix B
A diagram of the N/C system and the proposed system appears in Figure 5. The comparison assumes identical OCXOs in each system.
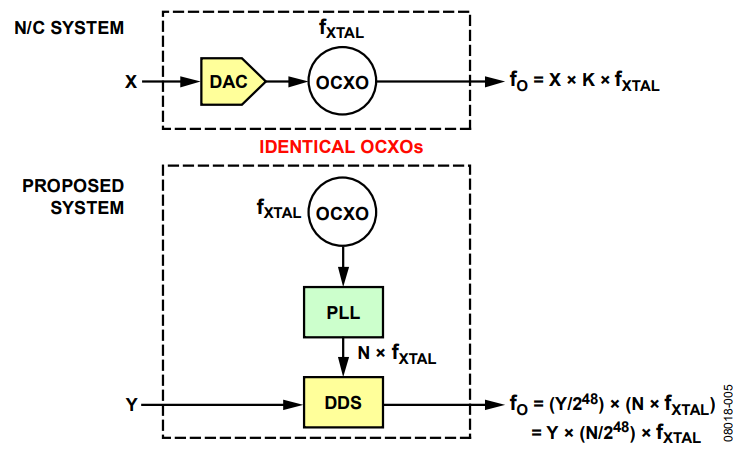
Figure 5. Voltage-Controlled OCXO vs. DDS.
The system parameter for the N/C system is the control word (X), which drives a DAC to alter the crystal resonant frequency (fXTAL) thereby producing the desired output frequency (fO). Note that fO is a scaler multiple of both X and K, where K is the product of the DAC gain and OCXO gain.
The system parameter for the proposed system is the DDS frequency tuning word (Y). The output frequency of the OCXO, in this case, is the crystal resonant frequency (fXTAL), which is free to drift because the OCXO operates open loop (its frequency control input is not used). The PLL represents the system clock generator in the AD9548 and synthesizes an integer multiple (N) of fXTAL. In this particular case, N = 100 because the PLL synthesizes a 1 GHz output signal from the nominal 10 MHz OCXO. The synthesized frequency serves as the sampling clock for the DDS. The DDS output frequency (fO) is a function of its sampling clock frequency (N × fXTAL, referring to Figure 5) and the value of the frequency tuning word (Y). Because the DDS in the AD9548 uses a 48-bit tuning word, the resulting expression for fO appears for the proposed system in Figure 5.
Note that in both the N/C and proposed systems, fO is a scalar multiple of the product of fXTAL and the system parameter (X or Y). In the N/C system, K is the scalar and has a value of 0.001 ppb/bit (see Appendix A). In the proposed system, the scalar is N/248, or 100/248 (which equates to 0.000355 ppb/bit). The key point is that the output of each system has the form
fO = α × β × fXTAL
where:
α is the system parameter.
β is a scalar.
This proves a linear relationship between the two system parameters. Therefore, the use of frequency tuning words (Y) is fundamentally identical to using DAC control words (X), except for a difference in system gain (the value of β). Furthermore, in the N/C system, β is device dependent because it is the product of the gain of the DAC and OCXO, both of which vary from device to device. Therefore, the N/C system requires calibration of β to ensure robustness. On the other hand, β is constant (N/248) in the proposed solution eliminating the need for calibration.
References
Nicholls, C.W.T. and G.C. Carleton. 2004. “Adaptive OCXO Drift Correction Algorithm.” Frequency Control Symposium and Exposition, 2004. Proceedings of the 2004 IEEE International: 509–517.
Kalman, R.E. 1960. “A New Approach to Linear Filtering and Prediction Problems.” Transactions of the ASME-Journal of Basic Engineering, 82 (Series D): 33–45.
Brown, R.G. and P.Y.C. Hwang. 1983. Introduction to Random Signals and Applied Kalman Filtering. John Wiley & Sons, Inc. ISBN 0471-52573-1.
Simon, D. 2001. “Kalman Filtering.” Embedded Systems Programming, 14 (6): 72–79.
Telcordia Technologies Generic Requirements. 2005. “Clocks for the Synchronized Network: Common Generic Criteria.” GR-1244-CORE, Issue 3.
Gouzhva, Y., A. Gevorkyan, and P. Bogdanov. 1992. “Accuracy Estimation of GLONASS Satellite Oscillators.” Frequency Control Symposium, 1992. 46th, Proceedings of the 1992 IEEE: 306–309.
