TNJ-048：LTspiceでサレン・キー型フィルタ（第5回）「サレン・キー型LPFの素子定数と伝達関数の関係を考える」

はじめに

何冊続くか分からない…、なんという、先の見えない（いいかげんな）という始まりでスタートしたこのフィルタ・シリーズ技術ノートも、もう 5 冊目です。

「何冊続くか分からない…」のとおり、事前に綿密に調整されている技術ノートではなく、執筆をしながら考えていき、答えを見つけていくというプロセスで進めています。そのため「犬も歩けば棒にあたる」という感じで、「ふーん、こういうふうになるんだな」という、自らの新たな発見にもなる、とても貴重な技術ノートなのでありました…。

今回の技術ノートの目的は…

この TNJ-048 でご紹介する内容のゴールを最初に示しておきます。TNJ-044 から TNJ-047 までで「伝達関数の分母 2 次式の部分をサレン・キー型 LPF で作りたい」なら「パラメータ ω₀と𝑄を求めればよい」という説明をしました。ここでは、このパラメータとサレン・キー型 LPF の素子定数がどのように関連しているかを考えてみます。その結果として、パラメータ ω₀と𝑄から素子定数を決定できるまでを説明していきましょう。

サレン・キー型 LPF の素子定数とパラメータω_𝟎と𝑸との関係を求めてみる

TNJ-044で「回路動作としては 2次サレン・キー型 LPFと、RLC 型 2 次 LPF とは等価」とお話し、TNJ-046 では、

任意の分母多項式によるカーブが与えられたとき
それは因数分解することができ（一般的には数値計算により）、分母が 1 次式と 2 次式の乗算になる
この 1 次式の部分は RC 型 LPF 1 段で、2 次式の部分はRLC 型の 2 次 LPF 1 段で実現できる
これらのフィルタをバッファを通してカスケード（従属）に接続していけば、その任意のカーブの分母多項式の特性をもつフィルタが実現できる
その 2 次式の部分をサレン・キー型 LPF で作りたいなら
2 次式の部分から極𝑠_𝑝±を得て
ω₀と𝑄を計算する
パラメータ ω₀と𝑄が分かれば、その特性を有する RLC 型2 次 LPF の RLC 定数が計算でき
それと等価なサレン・キー型 LPF も、ω₀と𝑄と素子定数との関係から計算できる

とお話しました。この説明から、「2 次式の部分をサレン・キー型 LPF で作りたい」なら「パラメータ ω₀と𝑄を求めれば素子定数が得られる」ことが分かります。

図1. サレン・キー型フィルタ（2 次フィルタ、LPF 形状。TNJ-044 の図2 再掲）

パラメータ ω₀と𝑄と素子定数との関係は、このフィルタ・シリーズの最初の TNJ-044 の式(3)、式(4)で既に示してあります。それさえ分かっていればよいのですが、そのなりたちを知るべく、ここではサレン・キー型 LPF の素子定数から、パラメータ ω₀と𝑄を求めてみます。

この関係が分かれば、上記でやりたいことが「きっちり」できるわけです（TNJ-044 でもう判明してはいますが…）。

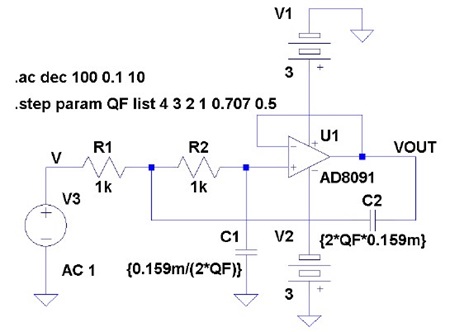
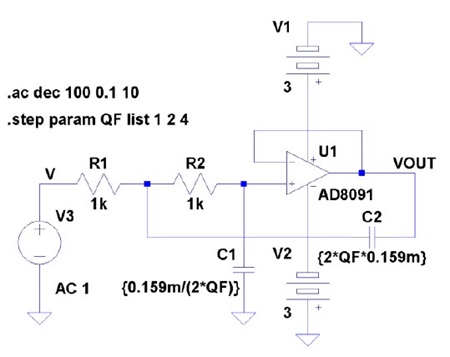
TNJ-044にも示した、サレン・キー型 LPFの回路図を図 1に示します。U1のOP アンプはゲイン = +1 のボルテージ・フォロワとなっています。OP アンプの反転増幅や非反転増幅の回路とは違い、これらの素子の組み合わせから伝達関数を計算するのはちょっと厄介な感じがしますね。

とはいえ少しがんばって計算してみましょう。解析のための回路図を図 2 に示します。

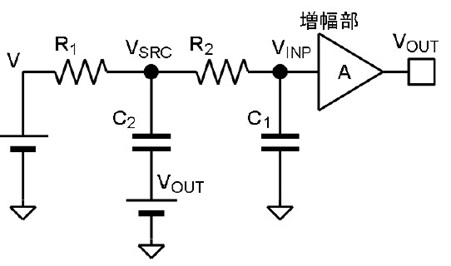
2 信号源による端子電圧は重ね合わせの理で計算できる

RC が 4つの、見た目簡単な回路ですが、式を立ててみましょう。そうすると結構手ごわいことに気がつきます。キルヒホッフの法則を用いても計算できるでしょうが、ここでは少し変化球で「テブナンの定理」と「重ね合わせの理」を応用して式をたててみます。

図 2 で増幅部と書いてあるところは、図 1 の回路図では、OP アンプがボルテージ・フォロワなのでゲイン𝐴 = +1なのですが、

式 1

こうしておきます。以降で OPアンプをボルテージ・フォロワとしない、ゲイン𝐴を持たせた場合で回路の振る舞いがどう変わるかを検討するために、このように定義しておきます。

重ね合わせの理を用いると回路計算がだいぶ簡単になります。入力信号𝑉と出力信号𝑉_𝑂𝑈𝑇が別々に RC 回路に加わったとして、ふたつの式を立てて、それを足し算（重ね合わせ）してみます。

最終目的は回路の式から伝達関数を求めること

図 2の増幅部の入力端子𝑉_𝐼𝑁𝑃、出力端子𝑉_𝑂𝑈𝑇の電圧、そして信号源𝑉の電圧を使って式を立てていきます。最終的に信号源𝑉の電圧と出力端子𝑉_𝑂𝑈𝑇の電圧の比、つまり回路の伝達関数を得るようにします。

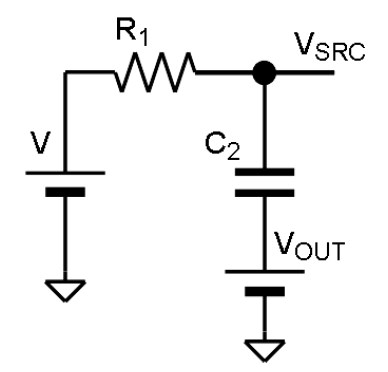
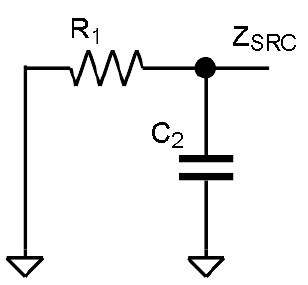
その計算の手始めとして、テブナンの定理としての R1, C2,𝑉, 𝑉_𝑂𝑈𝑇の等価回路を得るために、図 2 中の R1 と C2 によって端子𝑉_𝑆𝑅𝐶に現れる電圧と、その端子𝑉_𝑆𝑅𝐶から R1 と C2 を見た信号源インピーダンスを計算してみます。これは図 3 の計算をすることになります。実はここが「重ね合わせの理」を用いているところです。

まずは信号源𝑽のみが電圧をもつ条件での端子𝑽_𝑺𝑹𝑪の電圧の式をたてる

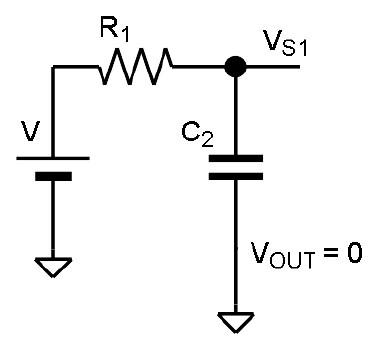
図 3 の回路において、𝑉のみが電圧をもち、𝑉_𝑂𝑈𝑇 = 0だと仮定します（図 4）。そうすると C2 がグラウンドに接続された状態として考えられます。電圧源はインピーダンスがゼロなので、このように考えることができます。このときの端子電圧𝑉_𝑆1は

式 2

ここでも𝑠はラプラス演算子で、𝑠 = 𝑗2𝜋𝑓 = 𝑗𝜔と考えてください。これは TNJ-045の式(18)と同じ形になっていることが分かります。

図3. 重ね合わせの理を使って𝑉𝑆𝑅𝐶を得る（電圧源シンボルは極性を明示する意味からDCのものを用いている） — 図3. 重ね合わせの理を使って𝑉_𝑆𝑅𝐶を得る（電圧源シンボルは極性を明示する意味からDCのものを用いている）

図4. 𝑉𝑂𝑈𝑇=0として𝑉からのみの𝑉𝑆1を得る（同） — 図4. 𝑉_𝑂𝑈𝑇=0として𝑉からのみの𝑉_𝑆1を得る（同）

図5. 𝑉=0として𝑉𝑂𝑈𝑇からのみの𝑉𝑆2を得る（同） — 図5. 𝑉=0として𝑉_𝑂𝑈𝑇からのみの𝑉_𝑆2を得る（同）

図6. 𝑉𝑆𝑅𝐶からみたインピーダンス𝑍𝑆𝑅𝐶を得る — 図6. 𝑉_𝑆𝑅𝐶からみたインピーダンス𝑍_𝑆𝑅𝐶を得る

つづいて出力信号𝑽_𝑶𝑼𝑻のみが電圧をもつ条件での端子𝑽_𝑺𝑹𝑪の電圧の式をたてる

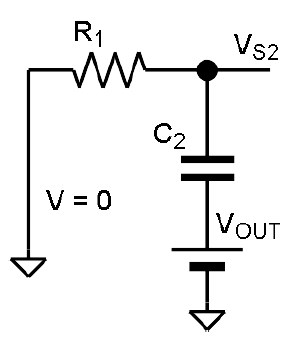
つづいて図 5 のように入力信号𝑉 = 0として、出力信号𝑉_𝑂𝑈𝑇のみが電圧をもったときの端子電圧𝑉_𝑆2の式をたててみます。

式 3

端子𝑽_𝑺𝑹𝑪から信号源𝑽を見たインピーダンスは

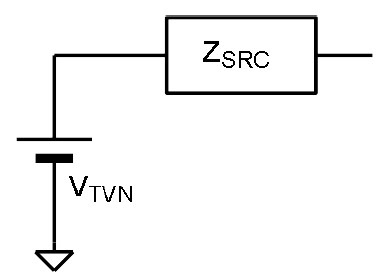
なお端子𝑉_𝑆𝑅𝐶から信号源𝑉を見たインピーダンス𝑍_𝑆𝑅𝐶は、R1, C2の並列接続になります。これを図 6 に示します。電圧源𝑉, 𝑉_𝑂𝑈𝑇はインピーダンスがゼロだとして取り扱います。

式 4

図7. テブナンの定理で𝑉𝑇𝑉𝑁と𝑍𝑆𝑅𝐶の回路になる（同） — 図7. テブナンの定理で𝑉_𝑇𝑉𝑁と𝑍_𝑆𝑅𝐶の回路になる（同）

図8. 全体は𝑉𝑇𝑉𝑁と𝑍𝑆𝑅𝐶の回路になる（同） — 図8. 全体は𝑉_𝑇𝑉𝑁と𝑍_𝑆𝑅𝐶の回路になる（同）

信号源𝑽と出力信号𝑽_𝑶𝑼𝑻が両方とも電圧をもつときの端子𝑽_𝑺𝑹𝑪の電圧𝑽_𝑻𝑽𝑵を重ね合わせの理から得る

重ね合わせの理により、入力信号𝑉と出力信号𝑉_𝑂𝑈𝑇が両方加わっているときの端子電圧𝑉_𝑇𝑉𝑁は

式 5

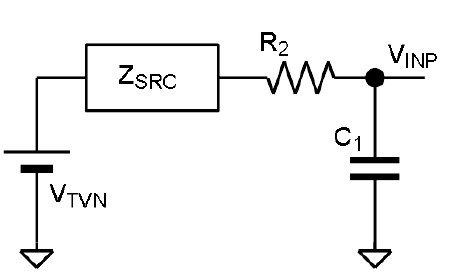
このようにすると図 7のように、電圧𝑉と 𝑉_𝑂𝑈𝑇、R1 と C2は、等価回路として信号源電圧𝑉_𝑇𝑉𝑁と信号源インピーダンス𝑍_𝑆𝑅𝐶に変換されることになります。ここが「テブナンの定理」となるところです。

さらに図 2 の回路全体は、図 7 の回路に R2 と C1 が直列に接続されている等価回路（図 8）になります。

以降、式中で操作するところを色づけして分かり易くします。

増幅部の入力端子に加わる電圧𝑽_𝑰𝑵𝑷を得ていよいよ伝達関数まで式変形していく

この図 8 の等価回路から、増幅部入力端子に生じる電圧𝑉_𝐼𝑁𝑃は（増幅部の入力インピーダンスが無限大だとすれば）

式 6

つづいて回路計算を簡単にするために（というか TNJ-044 で説明したように、同じ大きさの抵抗値とするため）

としてみます。式(6)に𝑉_𝑇𝑉𝑁も𝑍_𝑆𝑅𝐶も代入して

式 7

ここで式中の青色と緑色はそれぞれ𝑉_𝑇𝑉𝑁と𝑍_𝑆𝑅𝐶を指します。分母・分子に𝑅 + 1/𝑠𝐶₂を掛けて

式 8

系の伝達関数まで式変形していく

式(1)を𝑉_𝐼𝑁𝑃に代入し（赤色部分）

式 9-1

両辺に緑色部分を掛けると

式 9-2

右辺の𝑉_𝑂𝑈𝑇𝑅を左辺に移項してくくり、下記の緑色部分を整理すると

式 10

伝達関数の式になるように変形すれば

式 11

として伝達関数が得られ、また分母に 2 次多項式（赤色部分）が得られます。それでもなんだか面倒な式となりますね…。

分母の 2 次多項式だけをとりだして式変形していく

式(11)の赤色でハイライトした分母の部分を取り出します。

式 12-1

式 12-2

𝑠の次数の順番で並べなおして

式 12-3

𝑠²の項の係数を 1 にするためにくくりだすと

式 12-4

伝達関数の一般式と比較してサレン・キー型LPF の素子定数とパラメータ ω_𝟎, 𝑸との関係を求める

ここで TNJ-044 の式(14)と比較すると〔あらためて以下に式(13)としました〕

式 13

式(11)と式(12)から

式 14

素子定数とパラメータω_𝟎, 𝑸との関係が求められた

式(13)と式(14)から

式 15,16

が得られます。もう少しがんばってみると、

式 17,18

から、

式 19

という関係も導かれるわけです。

図 1の回路図のOPアンプがボルテージ・フォロワなので𝐴 = +1ですが、式(1)で示したように、図 2の増幅部でゲイン𝐴を持たせた場合には、LPF の出力として振幅が𝐴倍になるわけです。この𝐴倍は、上記の式(14)では、「伝達関数として単に𝐴倍になる」と考えればいいわけで、パラメータω₀と𝑄抽出の検討では考慮外としておけばよいのです。

さて、ここではとりあえず𝐴 = 1で式(19)を考え直してみると、

式 20

になります。

やってみれば何とか答えがでるもんだ

「一体何冊の技術ノートになるか見当がつきません」なんという、なんと行き当たりばったりな、むこうみず（？）な考えで進めてきたこのフィルタ・シリーズも、こつこつと式展開していってみると、ちゃんと答えが出るものですね（笑）。

図9. 私の人生にも大きな影響を与えた「男おいどん」（人に貸した第1集は帰ってこずに、これは最後の第6集）

どうでもいいはなしですが、ここまでの式展開は、アメリカ出張帰りの飛行機（ANA NH 5）の薄暗闇の中で、ワードの数式ツールを使って、式の導出と執筆を延々やっていたのです〔意外と腰を落ち着けて執筆作業をやっていない（汗）〕。PalmSprings という砂漠の都市で、WW（World Wide）のアナログ・デバイセズ社員 1500 人くらいを集めて行った WW SalesConference というものに、日本法人の多数のみんなと参加した帰りでした。

昔、私もおおいに影響を受けた、松本零士氏の「男おいどん[2]」という漫画（図 9）があります。この中で、主人公がいつもいくラーメン屋で食事をしていると「バイトするか？」と店主から勧められて、「調理場の様子を知ると、食う気がなくなる」（そして汚れきった、ゴミだらけの調理場のカットが… ^^;）というシーンがありました。なんだかその話しと重なるなあと（意外と腰を落ち着けて執筆作業をやっていないということで^^;）、独り薄暗闇の中で思ったのでした。

ああ、ライトが点いてオシボリが配られ始めた…。

これで与えられたパラメータω_𝟎, 𝑸から素子定数を求められることとなった

さて、式(17)

式 17-再掲

を使うと𝐶₁、𝐶₂を得ることができます。たとえば𝐶₁を得たいなら、上記式を変形し

式 21

これを式(20)に代入すると

式 22

これから

式 23

また𝐶₂は式(17)を自乗して式(23)を代入し、

式 24

これから

式 25

と得ることができます。これらの結果は TNJ-044 の式(3)、式(4)のとおりですね。

これにより、TNJ-046 と TNJ-047 で説明した、「2 次式の部分をサレン・キー型 LPF で作りたいなら、パラメータ ω₀と𝑄を求めればよい」というストーリーからすれば、式(23)と式(25)で（𝑅₁, 𝑅₂を、𝑅₁ = 𝑅₂ = 𝑅として固定したうえで）、それらのパラメータから素子定数を求めることができるわけです。

𝑸と𝑨とが与えられたときの素子定数を考える

ところで式(19)には1 − 𝐴という項（𝐴はアンプのゲイン）がありました。このうごきを𝑄との関係で少し考えてみたいと思います。

図 1 のようにサレン・キー型フィルタの OP アンプは（一般的には）ボルテージ・フォロワの構成にしますので、𝐴 = +1ですが、ここで+1以外にしたい場合もあるでしょう。特に以降の技術ノートで説明するように、ノイズ性能を最適化するときにこのテクニック（𝐴 > +1）を用いることができます。

さて、この式(19)は𝑄を求めるものでした。いっぽう𝑄 と𝐴が与えられたとき、 𝐶₁, 𝐶₂を求めることを考えてみます。式(19)を変形していきます。

式 26

ここで

式 26-1

とすれば

式 27

と変形できます。𝐶₁, 𝐶₂の比として𝑥で表します。さらに変形していくと、

式 28

この式の𝑥の解は実数、かつ正になる必要があります。解の公式を使って𝑥を求めてみると、

式 29

となります。𝐴 = 1のときは𝑥 (𝐶₁, 𝐶₂)は不定になりますが（ド・ロピタルの定理を使えばいいのですが…）、𝐴 > 1（つまり回路にゲインがある場合）であれば𝑥は実数になります。つまり「𝐴に関わらず式が有効」なことが分かります。

ここで右辺自体がマイナスなので、𝑥 > 0になるためには

式 30

の方が答えだろうと分かります。話しをもとに戻すと、これで

式 31

という関係を導くことができます。𝑥は𝐴と𝑄の関数でしたから、それぞれが決まれば、𝐶₁, 𝐶₂の比𝑥を求めることができるわけですね。𝐶₁, 𝐶₂と𝜔₀との関係は式(15)から得ることができます。

式 15-再掲

式(31)を変形していけば

式 32-1

ですから、これを式(15)に代入すると

式 32

と計算でき、𝐶₁は

式 33

として得ることができます。でも「こんな計算、何につかうのだ？」と思われるのではないでしょうか。通常は回路の仕様として𝑄と𝐴が与えられますから、この式で𝐴 > 1のときの素子定数を得ることができるわけです。実はそれ以外にも、以降の技術ノートの下ごしらえの意図もあるのでした（笑）。

𝑸と𝑨とが与えられたときの回路をシミュレーションで確認してみる

ここで得られた答えが正しいか、シミュレーションで確認してみましょう。図 10 はこれまで見てきたゲイン𝐴 = 1 の回路です（𝑄 = 1, 2, 4）。一方、図 11 はゲイン𝐴 = 2としてみた回路です。𝐴と𝑄 から式(30)で𝑥を求め、そこから式(32, 33)で𝐶₁, 𝐶₂を得ています。これで𝐴と𝑄 とが与えられたときのゲイン・ピークのようすを比較してみます。

図10. これまで見てきたゲイン = 1のサレン・キー型LPF（𝑄=1,2,4）

図12. 図10のゲイン = 1のサレン・キー型LPFのシミュレーション結果（𝑄=1,2,4）

図13. 図11のゲイン = 2のサレン・キー型LPFのシミュレーション結果（𝑄=1,2,4）

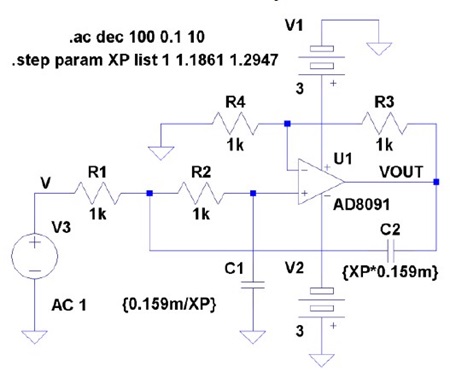
𝑄 = 1, 2, 4、𝐴 = 2が与えられたとき、式(30)から𝑥 = 1, 1.1861,1.2947 と計算できます。これを図 11 のシミュレーション回路中に.step コマンドのパラメータ XP として入れてあります。

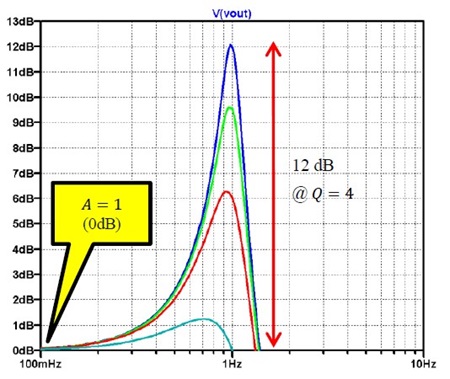
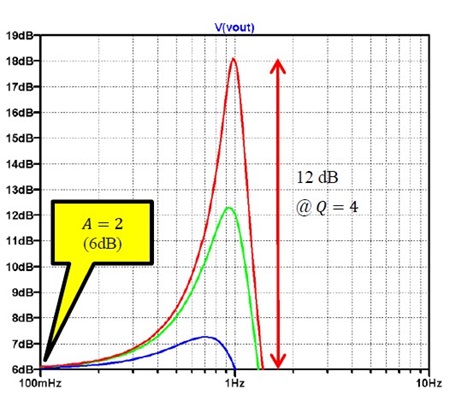
シミュレーション結果を図 12 と図 13 に示します。図 13 ではゲインが 6dB になっていますが、ゲイン・ピークはそれぞれ全く同じになっていることが分かりますね。

まとめ

この技術ノートの最初にお話ししたように、

任意の分母多項式によるカーブが与えられたとき
それは因数分解することができ（一般的には数値計算により）、1 次式と 2 次式の乗算になる
この 1 次式の部分は RC 型 LPF 1 段で、2 次式の部分はRLC 型やサレン・キー型の 2 次 LPF 1 段で実現できる
これらのフィルタをバッファを通してカスケード（従属）接続していけば、その任意のカーブの分母多項式の特性をもつフィルタが実現できる
その 2 次式の部分をサレン・キー型 LPF で作りたいなら
2 次式の部分から極𝑠_𝑝±を得て
ω₀と𝑄を計算する
パラメータ ω₀と𝑄が分かれば、その特性を有する RLC 型2 次 LPF の RLC 定数が計算でき
それと等価なサレン・キー型 LPF も、パラメータ ω₀,𝑄と素子定数との関係から計算できる

として説明してきました。答えを言ってしまえば単純な話で、このフィルタ・シリーズの最初、TNJ-044 の式(3)、式(4)でハナから説明していたわけですが、この技術ノート TNJ-048 でそのなりたちを詳しく考えてみました。なるほど、すべての辻褄があっていることが分かりました。

とくに𝐴 > 1のときに、フィルタ設計が難しいポイント（素子バラツキによる誤差）があり、実はこれも LTspiceを使ってモンテカルロ解析などでやってみたいところですが、それを始めると、このフィルタ・シリーズが終わらなくなってしまうのでした…（汗）

次の技術ノートでは

次の技術ノートでは「任意の多項式カーブから実際のフィルタを設計する」というお話しを、バタワース特性を例に説明してみたいところですが、ここまで数式が延々つづいた技術ノートでありましたので、皆様もちょっとお疲れかと思います。

そこで次の技術ノートでは LTspiceのノイズ解析機能を用いて、サレン・キー型 LPF のノイズ特性を考えてみるという話題に逸れてみたいと思います。実はこれがこのフィルタ・シリーズ最初の TNJ-044 にお話しした、「とある日のとある方との、とあるメールのやりとりで、横道の興味が湧いてきました」という、このフィルタ・シリーズにのめりこんでしまった根本の話題なのでした（笑）。